управление судном книга. На якоре 203 Штормовые диаграммы 184186 Штормовые условия в дрейфе

• Название: На якоре 203 Штормовые диаграммы 184186 Штормовые условия в дрейфе
• Анкор: управление судном книга.doc
• Дата: 19.12.2017
• Размер: 3.93 Mb.
• Имя файла: управление судном книга.doc
• Тип: Документы; #12203
• страница: 11 из 66

Данные, приведенные в табл. 5.1, содержат как отсчеты, получен­ные при измерениях, так и рассчитанные по ним дистанции и прямо­угольные координаты, приведенные к ЦТ судна.. Даны также углы отворота от начального курса ДК на каждый момент обсервации. За­меченные по секундомеру моменты пересчитаны относительно начала маневра. По рассчитанным прямоугольным кооргдинатам выполнена прокладка на планшете и получена траектория судна при выполне­нии циркуляции, показанная на рис. 5.3. На этом же планшете по­строены траектории судна при выполнении маневра пассивного тор­можения СПХ—ПХЗ. Для краткости данные траекторных измерений по двум указанным маневрам не приведены.

Начало координат для каждого маневра выбирается с таким рас­четом, чтобы траектория разместилась в желаемом месте планшета. В рассматриваемом случае (см. рис. 5.3) для маневров пассивного и активного торможения использовано общее начало координат, а для циркуляции выбрано отдельное начало.

Составление судовой информации. Траектории циркуляций судна (см. рис. 5.3) получены по обсервациям, сделанным в произвольные моменты времени. Следовательно, и углы изменения курса в этих точ­ках имеют случайные значения. *

Для получения точек с целочисленными значениями изменения курса и соответствующих этим значениям моментов* времени нужно выполнить приближенную интерполяцию между обсервациями, что позволит отметить нужные точки на траектории и рассчитать соответ­ствующие им моменты времени. Таким путем легко получить все необ­ходимые данные по поворотливости для включения в типовую форму судовой информации.

В принципе таким же способом можно построить и линейные гра­фики торможения. Рекомендуется следующий порядок построения ли­нейных графиков для каждого маневра торможения.




Рис. 5.4. Построение линейного графика торможения по графикам V(t) и s{t), получен­ным из натурных испытаний




Сначала по обсервованным точкам построить в прямоугольных ко­ординатах с помощью лекал сглаженный график s(t). Затем, снимая с этого графика отрезки пути, через равные промежутки времени, на­пример через 1 мин, рассчитать промежуточные значения скоростей и по ним построить график ,V(t). После этого, используя оба графика s(t) и V(t), легко яостроить линейный график торможения для вклю­чения в судовую информацию.

Построение линейного графика по данным траекторных измере­ний (см. рис. 5.3) для маневра СХП—ПХЗ показано на рис. 5.4.

3. 
   Расчетное и экспериментально-расчетное определение элементов поворотливости
   

В теории корабля существуют аналитические методы количест­венного расчета элементов поворотливости, однако точность результа­тов таких расчетов обычно невысока. Это объясняется сложным и еще недостаточно изученным характером совместного влияния многочис­ленных факторов на поведение судна при выполнении поворотов, что заставляет обращаться к натурному эксперименту.

К настоящему времени в нашей стране и за рубежом накоплен значительный объем экспериментальных данных по поворотливости различных судов, в том числе в виде траекторий, полученных при вы­полнении циркуляций с различными углами перекладки руля.

На основе обработки таких экспериментов в разное время и раз­ными авторами предложены эмпирические формулы для приближен­ного определения основных элементов циркуляции.

Из таких формул в качестве примера можно привести предложен­ные по результатам натурных испытаний одновинтовых судов разных серий (49 циркуляций на 11 судах), выполненных при различных уг­лах перекладки руля. Из большого числа факторов путем регрессной*

ного анализа были отобраны лишь наиболее значимые, что позволило получить сравнительно простые расчетные формулы.


V 5_Р -{- А,_р
Один из двух выбранных факторов — фактор корпуса и руля представляет собой комбинацию более простых факторов (см. п. 2.3) и определяется выражением

(5.10)

L

^где Ж ^{отношение} длины между перпендикулярами к ширине;

Он —- коэффициент полноты площади погруженной части ДП, рассчитываемой по формуле (2.5);

Х_Р — относительное удлинение руля, рассчитываемое по формуле (2.6);

5_Р—относительная площадь руля, выраженная в процентах к площади погружен-





В качестве второго фактора выбран угол дифферента судна i|>⁰, выраженный в градусах,


(5.11)
ф° -^йм- 57,3°,

где d_H и d_K — осадка носом и кормой (при дифференте на нос угол отрицателен).

С использованием указанных двух факторов получены структурно подобные эмпирические формулы для элементов циркуляции (см. п. 2.2), выраженных для сопоставимости в длинах судна. Эти форму­лы приведены ниже с указанными в скобках значениями стандартных относительных погрешностей (%):

Ф


(5.12)
/|=6,41—— 4-0,70ф° —0,93, (±9,0);

'о

/_t — 5,84 0,68ф° —2,15, (± 15,5);

У 6°

Ф

Ф
(5.13)

(5.14)

(5.15)

где 6° — угол перекладки руля.

Пользуясь фактором корпуса и руля Ф, можно также определить приближенно относительную скорость судна Р_уст (по отношению к начальной скорости) на установившейся циркуляции?

А

(5.16)
Г_уст= 1 - 0,056 —

Используя полученные по формулам (5.12) — (5.15) значения вы- двига 1\ прямого смещения h, тактического диаметра D_T и диаметра установившейся циркуляции 5_уСт, можно приближенно построить тра­екторию циркуляции одновинтового судна для заданных значений диф­ферента и угла перекладки руля.

По приведенным формулам рассчитаны элементы циркуляции с рулем, переложенных право на борт для теплохода «Большевик
М. Томас», и построена траектория, показанная на рис. 5.5 (условно принималось, что после поворота на 90° циркуляция переходит в устано­вившуюся).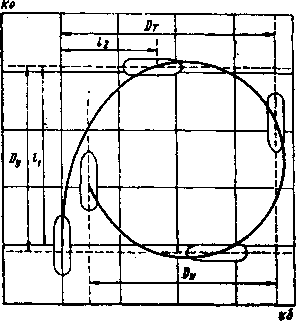




Рис. 5.5. Траектория циркуляции с рулем на борту теплохода «Больше»)» М. То­мас», построенная расчетным способом
Расчеты по формулам (5.12— 5.15) дают приближенные результа­ты, которые не могут в полной мере заменить результаты натурных наб­людений. Однако практически за­труднительно выполнить натурные испытания при различных осадках и дифферентах судна из-за боль­ших затрат эксплуатационного вре­мени. Поэтому обычно приходится ограничиваться экспериментальным определением элементов циркуля­ции только при какой-либо одной посадке судна. В этих случаях ис­пользование эмпирических формул в сочетании с экспериментальными значениями элементов циркуляции позволяет получить экспериментально-расчетные значения этих элемен­тов для любой заданной посадки судна. Для этого нужно сначала най­ти по формулам расчетные значения элементов для той же посадки и тех углов перекладки руля, которые были во время эксперимента, а за­тем рассчитать переходные коэффициенты:


V/.⁵
JL

г.

(5.17)

В приведенных выражениях в числителях стоят эксперименталь­ные, а в знаменателях расчетные значения элементов циркуляции.

Если из экспериментов обнаружилась существенная несимметрич­ность правых и левых циркуляций, то переходные коэффициенты еле* дует рассчитать отдельно для правых и левых поворотов.

Пользуясь полученными переходными коэффициентами, можно приближенно определить экспериментально-расчетные значения эле­ментов циркуляции для любой заданной посадки судна, если расчетные значения элементов для этой посадки умножить на соответствующие переходные коэффициенты, ранее полученные по формулам (5.17).

Полученные таким путем экспериментально-расчетные значения элементов циркуляции существенно точнее расчетных, а построенные по ним траектории сохраняют все особенности, присущие данному судну.

4. 
   Расчетное определение элементов торможения
   

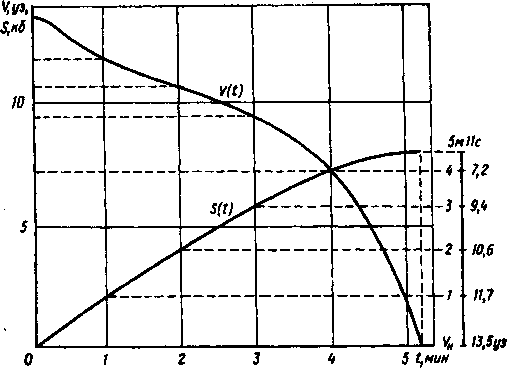
Для практического расчета ИТХ по приведенным в гл. 3 форму­лам необходимо определить коэффициент сопротивления корпуса и силу упора винта для данного судна.
Расчет коэффициента сопротивления корпуса. На основе регрес- . минного анализа результатов натурных наблюдений пассивного тор­можения на 18 одновинтовых морских судах разного типа было полу­пи подвыражение для коэффициента k (кг/м):

fc —5880-}-0,654Si -у, (5.18)

I•* - площадь смоченной поверхности, м²;

В

• 
  - отношение ширины судна к средней осадке.
  

Данная эмпирическая формула по статистической оценке позволя­ет определять коэффициенты сопротивления корпуса для одновиито- вых судов, а следовательно, и путь пассивного торможения со стан- 1артной относительной погрешностью около 9,4 %.

Площадь смоченной поверхности Й с достаточной для практи­ческих целей точностью рассчитывается по эмпирической формуле:


f 0,492-

(5,19)
0«--Д^2/3 ^4,854

и \ - нодоп*мсицение-судна, т.

Расчет максимальной силы упора винта на заднем ходу. Сила упо- ии вши а Ли**, которую развивает винт к моменту остановки судна

• 
  I liocnre.ibiio воды, т. е. когда скорость судна равна нулю, является нлой упора винта при нулевой поступи. Для изолированного винта, i е без учета взаимодействия с корпусом, сила упора при V=0 (ре- *им «на швартовах») с учетом (3.6) рассчитывается по формуле:
  

я_ш«-= */*>"* (6.20)

| и сила упора винга, работающего задним ходом н швартовном режиме с ча­

стотой л, Н;

А,, - коэффициент упора винта на заднем ходу в швартовном режиме.

Коэффициент упора k_p может быть выбран из специальных дна >рамм для расчета реверсирования винтов либо с достаточной для НФШ точностью рассчитывается по эмпирической формуле:

(н н \

0. 
   225 мп*—— i 0,098 sin —— ], (5.21)
   

//

I че — отношение шага кинти к его диаметру (шаговое отношение);

• н

0. 
   дисконое отношение;
   

г число лопастей.

Нели гребной винт имеет направляющую насадку, то полученный по формуле (5.21) коэффициент k_p следует уменьшись на 15%, т. е. \ множить на 0,85.

В реальных условиях на величину полезной силы упора при тор* можении оказывает влияние взаимодействие винта с корпусом судна. Как показал регрессионный анализ натурных наблюдений активного юрможении (25 экспериментов) на одновинтовых судах, чем больше площадь погруженной части мидель-шпангоута по сравнению с пло­щадью диска винта, тем большую полезную силу упора развивает пинт при торможении.
Влияние корпуса учитывается коэффициентом усиления упора С_уу, для расчета которого используется эмпирическая формула, получен­ная в результате регрессионного анализа,

St

Суу 0,508-1-0,106 ——, (5.22)

Ad

где S^r£ — площадь погруженной части мидель-шпангоута = рЗ'— коэффи­

циент полноты площади мидель-шпангоута), м²;

/ nD\ \

Ad — площадь диска винта I Ал^в —1. м².

Максимальная сила упора винта Р_тах рассчитывается по фор­муле:

^шах^^шв ^уу- (5.23)

Точность определения коэффициента С_уу по формуле (5.22) ха­рактеризуется стандартной относительной погрешностью, равной 12,3 %. Следовательно, с такой же точностью определяется и Ртах по формуле (5.23).

Расчет коэффициента активности торможения. По найденным значениям Ртах и k можно рассчитать коэффициент активности тор­можения:

о = , (5.24)

к (0,514V„)* ’ ^V V

где V_H — начальная скорость третьего периода, уз.

Расчетное определение времени и пути торможения судна. Как из­вестно (см. п. 3.3), процесс торможения состоит из трех периодов.

В первом периоде (период прохождения команды) скорость судна остается равной исходной скорости Vo. Достаточно задаться продол­жительностью первого периода t^l, чтобы определить путь s^l (величи­ну t^l рекомендуется принимать равной 5 с).

Время и путь второго и третьего периодов определяются по фор­мулам (3.32—3.38) в соответствии с рекомендациями, изложенными в пп. 3.1 и 3.3.

Полное время и полный путь торможения определяются как сум­ма соответствующих значений по трем периодам, т. е. по форму­лам (3.16).

Стандартная относительная погрешность расчетного пути второго периода т¹К™ равна погрешности расчета коэффициента сопротивле­ния, т. е., как было показано выше, составляет 9,4 %. Погрешность расчетного пути третьего периода зависит как от погрешности

коэффициента к, так и от погрешности расчетной силы упора, которая, как уже отмечалось, равна 12,3 %. С использованием этих значений пу­тем дифференцирования формулы (3.36) для активного тормозного пути по k и Ртах и перехода к конечным приращениям получено, что т^шотн = 8,0 % (для среднего значения а=1,6).

Точность расчета полного тормозного пути S зависит от соотно­шения между вторым s¹¹ и третьим $^ш участками тормозного пути. Стандартная ошибка полного тормозного пути М отн определяется по формуле (3.39).

При использовании характерного для большинства случаев тор- _su

можения диапазона —g— в пределах 0,15—0,75 получено:

Af_oTH = 6,4— 6,9%.

Статистическая оценка путем прямого сравнения расчетных тормоз­ных путей с экспериментальными полученными из многочисленных на­турных наблюдений подтверждает значение найденной стандартной по­грешности.

Универсальная диаграмма торможения и ее использование. Вместо расчетов по формулам (3.32—3.38) инерционно-тормозные характе­ристики можно получить по универсальной диаграмме (УД), приве­денной в прил. 4. УД построена по указанным формулам и позволяет определять время и путь как пассивного, так и активного тормо­жения.

Диаграмма состоит из двух независимых частей — верхней и ниж­ней, совмещенных на одном листе.

Нижняя часть служит для определения времени торможения или, вернее, вспомогательного произведения VJ, из которого затем опре­деляют t путем деления произведения V_Ht на известную начальную скорость V„ (V_H выражается в узлах, a t в секундах). В диаграмму входят с коэффициентом активности торможения а, после чего по за­данному относительному снижению скорости V/V_H и параметру Д/£ (А — водоизмещение в тоннах, к — коэффициент сопротивления в кг/м) находят вспомогательное произведение VJ.

Таким образом, нижняя часть диаграммы связывает функциональ­ной зависимостью четыре величины

VJV_a Мк V_Ht

и позволяет определить любую из этих величин, если известны три остальные.

Верхняя часть диаграммы связывает функциональной зависимо­стью четыре величины

а VfV „ Л/Л s

и предназначена для определения тормозного пути s (кб), но также позволяет определить и любую из этих четырех величин, если три остальные известны.

При использовании УД необходимо помнить, что при пассивном торможении коэффициент а всегда равен нулю.

Под скоростью V_H подразумевается начальная скорость пассив­ного или активного торможения в зависимости от периода, для кото­рого определяются элементы торможения.

Пример. Для контейнеровоза, характеристики которого даны в п. 5.2, рассчитать время и путь при торможении СХП—ПХЗ, если: на СХП V—13,5 уз; максимальная скорость, при которой возможен уверенный реверс, Ур«»9,4 уз; на ПХЗ номиналь­ная частота вращения винта n_a.x”«§3 об/мин.

По результатам расчета построить линейный график торможения для заданного маневра.

Решение. »

А. Определение коэффициента к и параметра Д/Л: