управление судном книга. На якоре 203 Штормовые диаграммы 184186 Штормовые условия в дрейфе

• Название: На якоре 203 Штормовые диаграммы 184186 Штормовые условия в дрейфе
• Анкор: управление судном книга.doc
• Дата: 19.12.2017
• Размер: 3.93 Mb.
• Имя файла: управление судном книга.doc
• Тип: Документы; #12203
• страница: 6 из 66

V*

Коэффициент активности торможения для разных конкретных ус­ловий может быть меньше единицы, больше единицы, равен единице или равен нулю. В каждом из перечисленных случаев меняется вид исходного уравнения (3.29), следовательно, меняется и вид его ре­шений.

Приведем решения уравнения (3.29) относительно времени и пути торможения в зависимости от значений константы а.

а < 1

(₁₊₁/ГГТ)(,. у ,/7П)

l„i У ^v- У • ^; (3.33)

Путь торможения при:

О < а 1

In Ц- ; (3.36)

2(1—в) „ V*

(1 —а) у_г -f- а

(■-*>

а — 1 m_xfk

(3.37)

2

а — О

^s=T^£'^,,1^_v^!"- ^(3-38)

Дифференциальное уравнение (3.29) и его решение (3.32—3.38) представляют собой математическую модель торможения, разрабо­танную в ОВИМУ на основе анализа результатов натурных испыта­ний судов.

Данная модель способна воспроизводить любое практически встречающееся изменение скорости при активном торможении. Это обеспечивается тем, что изменяющаяся по закону (3.27) сила упора винта в сумме с силой сопротивления (3.3) может давать суммарную тормозящую силу как возрастающую (а>1), так и снижающуюся (а< 1) в процессе торможения, т. е. описывать как выпуклые, гак и вогнутые графики V(t) разной степени кривизны вплоть до предель­ного случая, каковым является пассивное торможение (а=0).

Для наглядной оценки адекватности рассматриваемой математи­ческой модели ниже использованы результаты натурных испытаний торможения теплохода «Большевик М. Томас» водоизмещением 22 850 т.

На рис. 3.3 показано пассивное торможение судна ПХПм—Стоп, а на рис. 3.4 — торможение с реверсированием двигателя СХП—ПХЗ. Экспериментальные измерения пути и скорости показаны на обоих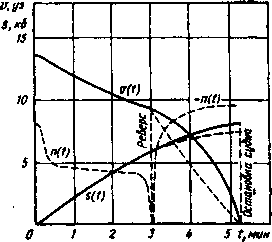

Рис. 3.4. Графики торможения теплохо­да «Большевик М. Томас» с реверсиро­ванием двигателя







Рис. 3.3. Графики пассивного торможе­ния теплохода «Большевик М. Томас»
рисунках черными точками, а графики s(t) и V(t), рассчитанные по формулам — сплошными линиями. Момент реверсирования (см. рис. 3.4) указан вертикальной штриховой линией. На обоих рисунках при­ведены также графики частоты вращения винта, построенные по ре­зультатам экспериментальных измерений.

На участке активного торможения от момента реверсирования до остановки судна (см рис. 3.4) для сравнения показаны штриховыми линиями также графики пути и скорости, построенные по формулам

25. 
    и (3.26).
    

Помимо описанных, существует еще ряд моделей, из которых можно отметить линейную математическую модель, в которой теку­щее значение силы сопротивления воды принято пропорциональным скорости судна в первой степени, т. е. R=KV (К — коэффициент со­противления при линейной зависимости, кг/с), а сила упора — посто­янной (Р,.= Р=const).

Имеющиеся результаты натурных экспериментов в виде элемен­тов пассивного и активного торможения по каждому испытанному судну позволяют получить статистические данные точности расчетных значений путей пассивного и активного торможения для каждой ма­тематической модели.

Как известно, в общем случае торможения полный тормозной путь содержит участки пассивного и активного торможения (второй и тре­тий периоды). Точность полного тормозного пути в соответствии с теорией ошибок можно оценивать по формуле

(3.39)


т¹¹ «^ш

отн *
где Мот -относительное среднее квадратическое отклонение (СКО) полного тор­мозного пути, %;

_отн — относительные СКО соответственно пассивного и активного тормозных путей, %;

s^N

• 
  отношение пассивного участка к полному тормозному пути;
  

m

“Тг —отношение активного участка к полному тормозному пути\


Таблица 3.1. Оценка точности математической модели торможения судба

Условное название математической модели	Относительное СКО, %
	тотн	И о тн	"отн
Линейная	16,5	16,0	13,04-13,8
ЦНИИМФ	8.4	21,7	8.3-М 8,3
ОВИМУ	8,4	5.4	4,8-т-6,4

Путь первого периода s¹ (прохождение команды) из-за его мало­сти на оценку точности практически не влияет.

Отношение i—. зависит от типа двигателя и его реверсивного

устройства, а также от начальной скорости судна. В реальных усло­виях это отношение находится в большинстве случаев в пределах 0,15-7-0,75. Для данных значений в табл. 3.1 приведены результаты оценки точности рассмотренных математических моделей для пассив­ных, активных и полных тормозных путей, выполненные на базе на­турных испытаний торможения с полного и полного маневренного хода на 16 различных судах с проведением надежных траекторных изме­рений.

Напомним, что при оценке точности расчетные тормозные пути определялись с использованием значений коэффициента сопротивления и силы упора винта, найденных из условия равенства между расчет­ным к экспериментальным временем торможения. Поэтому приведен­ные в табл. 3.1 оценки характеризуют потенциальную точность, с ко­торой каждая модель способна описывать процесс торможения судна при условии использования оптимальных значений коэффициента со­противления и силы упора винта.

Любая из рассмотренных математических моделей может быть использована для расчета ИТХ, если известны значения коэффициен­та сопротивления и силы упора винта для каждого конкретного судна при заданных условиях торможения. Эти необходимые значения могут быть найдены какими-то расчетными или экспериментально-расчетны­ми способами. Поскольку получаемые таким путем значения коэффи­циента сопротивления и силы упора винта будут содержать неизбеж­ные погрешности, т. е. не будут оптимальными, то ИТХ, полученные с их использованием, будут характеризоваться (статистически) боль­шими погрешностями, чем те, которые указаны в табл. 3.1.

Контрольные вопросы. 1. Каковы особенности реверсирования главного двигате­ля на теплоходах с гребным винтом фиксированного шага? 2. Из каких периодов в общем случае состоит процесс торможения судна? 3. Чем отличаются друг от друга основные математические модели торможения судна? 4. Как изменяется полезная си­ла упора винта в процессе активного торможения? 5. Как влияет загрузка судна на время и путь его торможения? в. Чем объясняется зависимость максимальной силы упора винта при активном торможении от осадки судна?

Глава 4. УПРАВЛЕНИЕ СУДНОМ В УСЛОВИЯХ ВЕТРА

1. 
   Силы и моменты, связанные с воздействием ветра
   

Сила ветра оценивается в баллах двенадцатибалльной шкалы, при­веденной в МТ-75.

Скорость ветра в судовых условиях измеряется над верхним мос­тиком с помощью анемометра. При этом измеряется так называемая кажущаяся скорость ветра UP, вектор которой представляет собой разность двух векторов — вектора истинного ветра ТГ_И и вектора ско­рости судна Р, т. е.

W = Wh-V. (4.1)

Вектор кажущегося ветра, помимо скорости, характеризуется кур­совым углом qw, т. е. углом между носовой частью ДП и кажущимся направлением ветра. За направление ветра принимается то, откуда ду­ет ветер (ветер дует «в компас»).

Курсовые углы ветра измеряются от 0 до 180° вправо и влево от ДП (курсовые углы правого или левого борта).

Геометрический смысл формулы (4.1) характеризуется векторным треугольником, показанным на рис. 4.1 (а, б, в). Из рисунка видно, что под влиянием движения судна вперед со скоростью V курсовой угол кажущегося ветра будет всегда меньше, чем истинного.

Аэродинамическая сила и ее момент. Равнодействующая сила давления ветра на надводную часть — аэродинамическая сила А не совпадает в общем случае с направлением кажущегося ветра, а откло­няется в сторону траверзного направления (см. п. 1.1).

Надводная часть судна находится в потоке воздуха под углом ата­ки, равным курсовому углу кажущегося ветра. При этом на надводной части создается аэродинамическая сила А, имеющая, как показано на рис. 4.2, продольную А_х и поперечную А_у составляющие.

Продольная составляющая А_х влияет на скорость судна, а попе­речная А_у вызывает боковое перемещение судна.

Поперечную аэродинамическую силу (Н) можно рассчитать по формуле

(4.2)

где Со* — безразмерный коэффициент поперечной аэродинамической силы, зависящий от формы надводной части судна и курсового угла кажущегося ветра;

Q_y— боковая площадь парусности (площадь проекции надводной части на ДП), м²;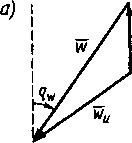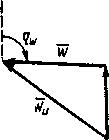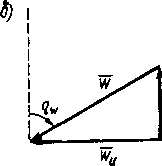


Рис. 4.1. Курсовой угол кажущегося ветра на движущемся судне
р_а —■ массовая плотность воздуха (р_в» 1,226 кг/м).
Безразмерный аэродинамический коэффициент С_ау по данным натурных и модельных исследований для разных судов находится обычно в пределах от 0,8 sin q_w до 1,3 sin q_w.


с?

		К
А		L

w

Рис. 4.2. Аэродинамическая сила и ее составляющие
Точка приложения аэродинами­ческой силы в соответствии со свой­ствами крыла смещается от ЦП на­встречу потоку воздуха (см. рис. 4.2), т. е. при носовых курсовых углах вет­ра в сторону носа, а при кормовых курсовых углах — в корму. Величина смещения зависит от курсового угла кажущегося ветра: чем острее угол атаки между ДП и направлением ветра, тем дальше от ЦП сме­щается точка приложения аэродинамической силы. Максимальное сме­щение точки приложения аэродинамической силы (при курсовых углах, близких к 0 и 180°) составляет в среднем приблизительно четверть длины судна, т. е. 0,25L, а при курсовых углах кажущегося ветра, рав­ных 90°, точка приложения аэродинамической силы совпадает с ЦП.

Таким образом, в общем случае на корпус судна действует не только поперечная аэродинамическая сила, вызывающая дрейф судна, но и момент этой силы, стремящийся развернуть судно вокруг верти­кальной оси, проходящей через ЦТ.

Плечо поперечной аэродинамической силы 1_Л относительно ЦТ можно определить по приближенной формуле:


(4.3)
7 -о I^е, I ^<ци 4w

/_д-0,25+ _L ^