ответы по ОЗЗ. Общественное здоровье и здравоохранение как наука и предмет преподавания и ее методы

• Название: Общественное здоровье и здравоохранение как наука и предмет преподавания и ее методы
• Анкор: ответы по ОЗЗ
• Дата: 02.11.2022
• Размер: 0.92 Mb.
• Имя файла: OZZ_-_otvety.docx
• Тип: Документы; #767657
• страница: 3 из 20

Единица наблюдения – первичный элемент статистической совокупности, наделенный всеми признаками, подлежащими изучению и регистрации.

Программа сбора материала представляет собой последовательное изложение учитываемых признаков – вопросов, на которые необходимо получить ответы при проведении данного исследования. Это может быть специально составленный исследователем опросный лист, анкета, карта. Документ должен иметь четкое название. Вопросы должны быть четкими, краткими, соответствовать целям и задачам исследования; на каждый вопрос следует предусмотреть варианты ответов.

А при клинико – статистическом методе:

Сравнивается не менее 2 групп,

Группы максимально похожи и приближены (по полу, возрасту и т.д.),

Сравниваются 2 фактора (лекарство, метод – по поводу улучшения),

Группы обычно маленькие, до 30 человек; поэтому при расчетах – средние величины для малых значений.
10. Статистическая совокупность и ее групповые свойства (распределение признака, среднее значение, изменчивость, ошибка репрезентативности, связь между признаками).

Статистическая совокупность—  это группа относительно однородных элементов, взятых вместе в конкретных границах пространства и времени и обладающих признаками сходства и различия.

Виды:

Генеральная совокупность - совокупность единиц, подлежащая изучению, ее численность обозначается N.

Выборочная совокупность - часть единиц генеральной совокупности, отобранная в случайном порядке, ее численность обозначается n. Выборочное наблюдение - не сплошное наблюдение, при котором обследованию подвергается оп­ределенная часть единиц изучаемой совокупности, отобранная в случайном порядке.
Основные свойства статистической совокупности:

Первое свойство характеризует распределение признаков и может быть выражено абсолютными числами или показателями. Элементы совокупности распределяются неодинаково (по характеру) учетного признака, образуя определенную структуру (например, здоровые–больные). Это свойство позволяет использовать относительные величины, стандартизованные показатели, вариационный ряд.

Второе свойство определяется средним уровнем признаков и характеризуется различными средними величинами. Обобщенная характеристика различных величин количественного учетного признака совокупности (критерии: средняя арифметическая — М, мода — Мо, медиана — Ме).

Третье свойство определяет разнообразие (вариабельность) признаков. Различие единиц наблюдения по величине учетного количественного признака совокупности (критерии: лимит — Lim, амплитуда — Ampl, среднее квадратическое отклонение — σ, коэффициент вариации — Сv).

Четвертое свойство характеризует репрезентативность или представительность признаков и включает определение ошибок средних и относительных величин, доверительных границ средних или относительных величин, достоверности разности средних или относительных величин по критерию t.

Типы репрезентативности:

–количественная — достаточный объем (n) наблюдений в выборочной совокупности, гарантирующий получение статистически достоверных данных;

–качественная — типичность структурного соответствия признаков всех единиц наблюдения в выборочной и генеральной совокупности, достигается путем специальных методов отбора элементов выборочной совокупности из генеральной.

Пятое свойство определяется взаимосвязью между признаками (корреляция) и характеризуется с помощью коэффициентов корреляции.Зависимость

размеров признаков друг от друга (критерии: коэффициент корреляции — rxy, коэффициент ранговой корреляции — ρxy, коэффициент регрессии — Rxy, коэффициент согласия — χ2)

Единица наблюдения — первичный элемент статистической совокупности, наделенный признаками сходства и различия.

Признаки сходства — общие учетные признаки, свидетельствующие о принадлежности конкретной единицы наблюдения

кэтой совокупности. Эти признаки описывают обязательное условие статистического наблюдения: единство времени и места исследования.

Признаки различия — представляют индивидуальные особенности (характеристики) каждой единицы наблюдения, являются конечным объектом статистического исследования. Признаки различия подлежат изучению и регистрации, поэтому называются учетными признаками.

По характеру учетные признаки могут быть:

–количественные (определительные) — признаки, значения которых имеют числовое выражение (рост, масса тела, частота пульса и др.);

–качественные (атрибутивные) — признаки, значения которых определяются вербально (пол, образование, диагноз и др.).

По роли в совокупности учетные признаки подразделяются на:

–факторные — признаки, влияющие на изменение зависимых признаков, вызывают действие;

–результативные — зависимые признаки, изменяющие свое значение под влиянием других, факторных признаков

11. Альтернативный анализ. Относительные величины и их виды, методика вычисления и применение в медицинской практике.

Альтернативный анализ - когда событие может наступить, но может и не произойти (рождение, заболевание, смерть).

Относительные величины характеризуют распределение признака, отражают качественный состав совокупности, но в отличие от абсолютных величин учитывают общий размер совокупности.

Виды относительных показателей.

Относительные величины, применяемые в медицине разделяются на следующие виды показателей:

• 
  экстенсивные показатели;
  
• 
  интенсивные показатели;
  
• 
  показатели соотношения;
  
• 
  показатели динамического ряда.
  

Экстенсивные показатели (или коэффициенты) характеризуют внутреннюю структуру явления, определяя удельный вес или долю изучаемого явления (части явления) по отношению к целому, к размеру изучаемой статистической совокупности (например, структура заболеваемости, смертности, доля заболевших среди вакцинированных, удельный вес умерших среди прооперированных больных и т.п.).

Интенсивные показатели (или коэффициенты) характеризуют частоту (интенсивность, уровень, распространенность) явления за определенный промежуток времени в изучаемой среде, в которой оно происходит и с которой оно (явление) непосредственно связано. Типичными интенсивными показателями являются демографические показатели (рождаемость, смертность) и показатели заболеваемости (первичная заболеваемость, общая заболеваемость).

Показатели соотношения (коэффициенты) характеризуют частоту встречаемости признака в статистической совокупности, его распространенность и применяются в том случае, когда сравниваются две, не связанные между собой статистические совокупности, но сопоставимые логически и по содержанию (число врачей, среднего медицинского персонала, больничных коек на количество населения, число операций в расчете на определенное число населения и т.п.). Показатели соотношения отличаются от показателей интенсивности по содержанию, но схожи с ними по методике вычисления.

Динамический ряд – это совокупность однородных статистических величин, показывающих изменение какого-либо явления (признака) во времени. Числа, из которых составляется динамический ряд, могут быть представлены абсолютными, средними и относительными величинами.

Показатели динамического ряда (наглядности, роста, прироста) характеризуют изменение абсолютных и относительных показателей во времени (динамике).

Различают простые динамические ряды (состоит из абсолютных величин) и сложные или производные (состоит из средних и относительных величин); моментные (состоит из величин, характеризующих явление на определенный момент времени (на конец декады, месяца, года и т.д.) и интервальные (состоит из величин, характеризующих явление за определенный промежуток (интервал) времени (сутки, неделя, месяц, год и т.д.).

Методы расчета относительных показателей.

При вычислении экстенсивных показателей необходимо знать абсолютный размер явления и абсолютный размер части явления, то есть используют только одну статистическую совокупность и ее составные части. Большинство экстенсивных показателей определяется в процентах (%) и долях единицы.

Вычисление производят по формуле:

Размер части явления

Эк стенсивный показатель = х 100 (в %).

Размер явления в целом

При вычислении интенсивных показателей необходимо знание двух статистических совокупностей, одна из которых представляет среду, другая – явление. В демографической и санитарной статистике в качестве среды чаще всего рассматривается население, в качестве рассматриваемых явлений – число рождений, смертей, заболеваний, осложнений и т.п. Как правило, большинство интенсивных показателей рассчитывают на 1000 населения (в ‰), на 10 000 или на 100 000 населения).

Вычисление производят по формуле:

Размер изучаемого явления

Ин тенсивный показатель = х 1000 (в ‰).

Размер среды

Показатели соотношения отличаются от показателей интенсивности по содержанию, но схожи с ними по методике вычисления и рассчитываются по формуле:

Размер изучаемого явления

По казатель соотношения = х 10 000.

Размер среды

Методы расчета показателей динамического ряда.

С целью изучения особенностей исследуемого процесса и достижения наглядности в характеристике изучаемого явления используется расчет показателей динамического ряда:

• 
  абсолютный прирост;
  
• 
  темп прироста (или убыли).
  
• 
  показатель роста (или снижения);
  
• 
  показатели наглядности;
  

Абсолютныйприрост представляет собой разность между последующим и предыдущим уровнем динамического ряда. Измеряется в тех же единицах, что и уровни динамического ряда.

Темп прироста (или убыли) показывает отношение абсолютного прироста (или снижения) (разности между последующим и предыдущим уровнем динамического ряда) к предыдущему уровню, принятому за 100%.

Показатель (критерий) роста (или снижения) вычисляется как отношение каждого последующего уровня динамического ряда к предыдущему, принятому за 100%.

Показатель (критерий) наглядности показывает отношение каждого уровня к начальному уровню динамического ряда (первое значение), принятому за 100%.
12. Вариационный анализ. Средние величины и их виды, методика вычисления и применение в медицинской практике.

Средние величины дают обобщающую характеристику статистичес­кой совокупности по определенному изменяющемуся количественному признаку. Средняя величина характеризует весь ряд наблюдений одним чис­лом, выражающим общую меру изучаемого признака. Она нивелирует случайные отклонения отдельных наблюдений и дает типичную харак­теристику количественного признака.

Требования к средним величинам:

1) качественная однородность совокупности, для которой рассчиты­вается средняя величина - только тогда

она будет объективно отображать ха­рактерные особенности изучаемого явления.

2) средняя величина должна основываться на массовом обобще­нии изучаемого признака, т.к. только тогда она выражает типич­ные размеры признака

Средние величины получаются из рядов распределения (вариа­ционных рядов).

Вариационный ряд- ряд однородных статистических величин, ха­рактеризующих один и тот же количественный учетный признак, отли­чающихся друг от друга по своей величине и расположенных в опре­деленном порядке (убывания или возрастания).

Элементы вариационного ряда:

а) варианта - v - числовое значение изучаемого меняющегося коли­чественного признака.

б) частота - p (pars) или f (frequency) - повторяемость вариант в вариационном ряду, показывающая, как часто встречается та или иная варианта в составе данного ряда.

в) общее число наблюдений- n (numerus) - сумма всех частот: n=ΣΡ. Если общее число наблюдений более 30,статистическая выборка считается большой, если n меньше или равно 30 - малой.

Вариационные ряды бывают:

1. в зависимости от значения варианты:

а) прерывные (дискретные), состоящие из целых чисел

б) непрерывные, когда значения вариант выражены дроб­ным числом. В прерывных рядах смежные варианты отличаются друг от друга на целое число (число ударов пульса, число дыха­ний в минуту, число дней лечения). В непрерывных рядах ва­рианты могут отличаться на любые дробные значения единицы.

2. в зависимости от частоты встречаемости признака:

а) простой - ряд - каждая варианта встречается один раз, т.е. частоты равны единице.

б) обычный - ряд, в котором варианты встречаются более одного ра­за.

в) сгруппированный- ряд, в котором варианты объединены в группы по их величине в пределах определенного ин­тервала с указанием частоты повторяемости всех вариант, входящих в группу.

Сгруппированный вариационный ряд используют при большом числе наблюдений и больном размахе крайних значений вариант.

Обработка вариационного ряда заключается в получении парамет­ров вариационного ряда (средней величины, среднего квадратичес­кого отклонения и средней ошибки средней величины).

3. в зависимости от числа наблюдений:

а) четные и нечетные

б) большой (при числе наблюдений больше 30) и малый (если число наблюдений меньше или равно 30)

Виды средних величин:

а) мода (Мо) - величина признака, чаще других встречающаяся в со­вокупности. За моду принимают варианту, которой соответствует наибольшее количество частот вариационного ряда.

б) Медиана (Me) - величина признака, занимающая срединное значе­ние в вариационном ряду. Она делит вариационный ряд на две рав­ные части.

На величину моды и медианы не оказывают влияния числовые зна­чения крайних вариант, имеющихся в вариационном ряду. Они не всегда могут точно характеризовать вариационный ряд и применяют­ся в медицинской статистике относительно редко. Более точно ха­рактеризует вариационный ряд средняя арифметическая величина.

в) Средняя арифметическая(М, или  ) - рассчитывается на осно­ве всех числовых значений изучаемого признака.

Реже применяются другие средние величины: средняя геометрическая (при обработке результатов титрования антител, токсинов, вакцин); средняя квадратическая (при определении среднего диаметра среза клеток, результатов накожных иммунологических проб); средняя кубическая (для определения среднего объема опухолей) и другие.

В простом вариационном ряду, где варианты встречаются только по одному разу, вычисляется средняя арифметическая простая по формуле: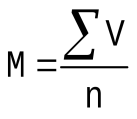

, где V - числовые значения вариант, n - число наблюдений, Σ - знак суммы

В обычном вариационном ряду вычисляется средняя арифметичес­кая взвешенная по формуле:

, где V - числовые значения вариант, р - частота встречаемости вариант, n - число наблюдений.

Средние величины являются важными обобщающими характеристика­ми совокупности. Однако за ними скрываются индивидуальные значе­ния признака. Средние величины не показывают изменчивости, колеб­лемости признака. Если вариационный ряд более компактен, менее рассеян и все от­дельные значения расположены вокруг средней, то средняя величина дает более точную характеристику данной совокупности. Если вариа­ционный ряд растянут, отдельные значения значительно отклоняются от средней, т.е. имеется большая вариабельность количественного признака, то средняя менее типична, хуже отражает в целом весь ряд.

Одинаковые по величине средние могут быть получены из рядов с различной степенью рассеяния, поэтому для характеристики вариационного ряда, помимо средней величины, необходима другая характеристика, позволяющая оценить степень его колеблемости.

Простыми показателями, характеризующими разнообразие признака в изучаемой совокупности, являются

а) лимит - минимальное и максимальное значение количественного признака

б) амплитуда - разность между наибольшим и наименьшим значением вариант.

Применение средних величин:

а) для характеристики физического развития (рост, вес, окружность груди, динамометрия)

б) для оценки состояния здоровья человека путем анализа физиологических, биохимических параметров организма (уровня АД, ЧСС, температуры тела)

в) для анализа деятельности медицинских организаций (среднее число дней работы койки в году и т.д.)

г) для оценки работы врачей (среднее число посещений на одного врача, среднее число хирургических операций, среднечасовая нагрузка врача на приеме в поликлинике)
13. Репрезентативность признака. Статистическая оценка достоверности результатов исследования. Параметрические критерии оценки достоверности результатов исследования.

В статистических исследованиях применяют 2 вида наблюдений: сплошное и выборочное. Самые надежные результаты можно получить при применении сплошного метода, т. е. при изучении всей генеральной совокупности. Изучение генеральной совокупности значительно трудоемко. Поэтому в исследованиях применяют выборочные наблюдения, охватывающие только часть генеральной совокупности. При исследовании следует обеспечить репрезентативность выборочных наблюдений (представительность по отношению к генеральной совокупности, частью которой она является). С тем, чтобы полученные при изучении выборочной совокупности данные можно было перенести на генеральную совокупность, необходимо провести оценку достоверности результатов статистического исследования. В ходе исследования могут возникнуть погрешности, называемыми ошибками репрезентативности. Они находятся в прямо пропорциональной зависимости от величины среднего квадратического отклонения: она тем больше, чем больше среднее квадратическое.

- Критерий достоверности (Стьюдента) определяется как величина разности средних величин или показателей, деленная на извлеченную из квадратного корня сумму квадратов ошибок средних арифметических.

т = M1 – M2 / √ m1^2 +m2^2

- Средняя ошибка средней арифметической равняется отношению среднеквадратического отклонения к квадратному корню из числа наблюдений.

m= δ/√n,

- Средняя ошибка показателя (относительных величин) рассчитывается путем извлечения квадратного корня из величины показателя, умноженного на разницу 100% и величины данного относительного показателя, деленного на число наблюдений.

m = √p·q / n

Критерий Стьюдента должен быть равен или больше цифры 2. Только при этих условиях прогноз в 95% и более считается безошибочным, свидетельствующим о надежности используемого нового метода (лекарственного препарата, факторов риска, гигиенических характеристик).