Метод виклад з мат-ки 2. Спеціальна методика викладання математики зміст методика розв'язування арифметичних задач
 Скачать 7.16 Mb.
|
|
Таблиця заповнюється по мірі вивчення чисел. Краще, коли вона зроблена у вигляді набірного полотна. Тоді вчитель може запропонувати учням виконати такі завдання:
Якщо можна зробити таблиці менших розмірів індивідуально для кожного школяра, це б дозволило їм повторювати роботу учня, викликаного до дошки і краще усвідомлювати числовий ряд. Потрібно показати розумово відсталим школярам, що верхній і нижній ряди таблиці мають багато спільного, але встановити це діти повинні по можливості самостійно. Якщо вони цього не помічають, тоді вчитель пояснює, що:
На такій таблиці зручно показати різницю між одноцифровими і двоцифровими числами. На ній чітко видно, що якщо множина предметів записується одним арифметичним знаком, однією цифрою - це число називається одноцифровим, а якщо двома - двоцифровим. Отже, числа від 1 до 9 є одноцифровими, а числа від 10 до 20 - двоцифровими. Для закріплення цих знань доцільно провести лабораторно-практичне заняття, на якому школярі визначають на слух одноцифрові і двоцифрові числа, показують і називають найменше та найбільше одноцифрове і двоцифрове число, визначають кількість одиниць і десятків у числах, знаходять пропущені та сусідні числа. записують їх у порядку зростання або спадання тощо. У 2-му класі не закінчується робота над встановленням залежностей між числом, цифрою і кількістю. Для цього педагог використовує різні множини предметів, закріплює усвідомлення того, що кількість не пов'язується з місцем, яке вони посідають у просторі. Такі заняття необхідні для розумово відсталих учнів, адже через особливості свого психічного розвитку вони швидко забувають матеріал. Для цього доцільно давати учням завдання, які б виконувались через використання різних посібників: відкласти число на абаку, на рахівницях, на паличках, на лінійці, на монетній касі тощо. Крім знання місця числа в числовому ряді учні повинні засвоїти місце одиниць і десятків у числі. Для цього можна використати таблицю розрядів, виконану у вигляді набірного полотна даного зразка: Таблиця 4.3.
З його допомогою складається двоцифрове число, визначають місце одноцифрового числа. Ця таблиця полегшує порозрядне порівняння чисел. Діти зможуть зробити висновок: у кожному числі є десяток: всі числа двоцифрові: у верхньому числі одна одиниця, у середньому - три. у нижньому - п'ять, отже, нижнє число більше за попередні. Для кращого засвоєння десяткового складу потрібно вчити учнів складати числа, використовувати  При порівнянні чисел у 2-му класі школярі використовують знаки „>” (більше), „<” (менше), „=” (дорівнює). Не дивлячись нате, що вони познайомились з ними у 1-му класі, вчитель знову ж таки повинен повернутись до їхнього пояснення. Порівнюючи числа 2-го десятка, спочатку він вибирає її з них, які стоять поруч один одного і для порівняння яких потрібно врахувати властивості числового ряду. Потім вчить порівнювати між собою одноцифрові і двоцифрові числа, формуючи у розумово відсталих поняття про те, що при їх порівнянні завжди більшим буде двоцифрове. Порівнюючи числа 2-го десятка, потрібно вимагати від школярів відповіді на запитання: "На скільки одиниць перше число більше за друге?". "На скільки одиниць друге число менше за перше?". Деякі випадки порівняння чисел учні допоміжної школи вже у 2-му класі повинні завчити. Наприклад: будь-яке число більше нуля (0< ). Школярі вивчають, що коли в рамочку вставити будь-яке число, то воно буде більше за 0. Для закріплення знань про місце числа у натуральному ряді чисел учням пропонуються такі вправи. 1) знайдіть пропущені числа:
2) знайдіть сусідів числа:
Робота над числами другого десятка ведеться і в плані закріплення навичок свідомого рахунку. Учні повинні вміти вести рахунок як у прямому, так і у зворотному напрямку, не лише від 1. але й від будь-якого заданого числа; прилічувати й відлічувати не лише по одиниці, але й рівними числовими групами, з застосуванням наочних посібників (на початкових етапах роботи), і без опори на них. Після ознайомлення школярів з письмовою нумерацією чисел до 20 організовується робота над аналізом чисел за їхнім десятковим складом. Для цього учням пропонується розкласти числа на розрядні одиниці. Наприклад: 15 – це 1 дес. і 5 од.; 10 і 5 – це 15. Вивчення нумерації поступово підводить школярів до дій першого ступеня, обчислення яких в своїй основі містить знання про утворення натурального ряду чисел і десяткового складу чисел (11 + 1, 12 – 1; 10 + 3; 3 + 10; 13 – 3; 13 – 10). Корисними також в цей період над числами першого і другого десятка є вправи на співставлення: 3+1=4 4-1=3 13 + 1 = 14 14-1 = 13 4.3. Додавання і віднімання у межах 20 З діями першого ступеня діти допоміжної школи знайомляться у другому класі. Оволодіння обчислювальними прийомами базується на знаннях вихованцями дій додавання і віднімання в межах 10 та нумерації і складу чисел другого десятка. Так само, як і в попередній рік навчання, вчитель використовує велику кількість наочних посібників. Дії додавання і віднімання вивчаються паралельно – випадки віднімання розглядаються за відповідними випадками додавання. У другому класі учні вивчають назви компонентів цих арифметичних дій, вчаться вводити їх у своє мовлення. Для кращого їх запам'ятовування учитель залучає наочність у вигляді таблиць. Таблиця 4.4.
Числа, які потрібно додати, називають доданками, а результат додавання називають сумою.    Таблиця 4.5.
Число, від якого віднімають, називається зменшуваним; число, яке віднімають - від'ємником; число, яке одержують в результаті віднімання - різницею. Вивчення дій додавання і віднімання здійснюється у два етапи. Спочатку учні обчислюють приклади діями першого ступеня в межах 20 без переходу через розряд, потім - з переходом через розряд. Розглянемо конкретно кожен етап. 1) Додавання десятка з одноцифровими числами та віднімання від двоцифрового числа одного з його розрядів: 10 + 4; 4 + 10; 14 – 4; 14 – 10. Розв'язування прикладів цього типу здійснюється на основі знань десяткового складу числа. Навчальним посібником можуть бути рахункові палички. Вчитель бере пучечок паличок (1 десяток) і поруч викладає ще 4 палички. Оскільки учні вже вчили нумерацію і утворення чисел другого десятка, знайомі з отриманням двоцифрового числа і з його десятковим складом, то обчислення прикладів цього типу не викликає у них значних труднощів, їм пропонується назвати отримане число, скласти приклад і записати в зошит: 10 + 4 = 14. При вирішенні прикладів типу 4+10 необхідно користуватися законом перестановки доданків. Учням пропонується перекласти 4 палички після пучечка (десятка). Підрахунок показує, що паличок залишилось стільки ж, скільки й було. На даному етапі можна використати і таблички цифрової каси, використовуючи які при додаванні учень накладає табличку з цифрою одиниць на нуль таблички з позначанням десятка.  Цей прийом є особливо ефективний для тієї групи учнів, які недостатньо усвідомили десятковий склад числа і під час запису результатів допускають помилки, наприклад 10 + 7 = 107. При поясненні обчислення прикладів на віднімання від двоцифрового числа десятка або кількості його одиниць також можна використати рахункові палички. Вчитель, наприклад, набирає число 14 (1 пучечок і 4 палички), аналізує його, після чого пропонує учням забрати 1 пучечок (1 десяток) і прорахувати, скільки паличок залишилось. Складається приклад: 14 – 10 = 4. Аналогічним чином пояснюється віднімання від числа 14 кількість його одиниць: 14 – 4 = 10. В цей період учні також обчислюють приклади, вирішення яких в своїй основі передбачає закріплення знань про властивості числового ряду і нумерацію чисел в межах 20. Це приклади типу 12 + 1, 13-1, 15 + 1, 16–1. 2) Додавання і віднімання без переходу через розряд. Пояснення обчислення прикладів даного типу проводиться у такій послідовності. а) додавання до двоцифрового і віднімання від двоцифрового числа одноцифрового. Спочатку розглядаються випадки додавання, у яких число одиниць першого доданка більше одиниць другого доданка: 15 + 4, 16 + 2, 17 + 2І лише потім включати випадки типу 11 + 6, 13 + 5, де число одиниць першого доданку менше числа одиниць другого, хоч прийоми їхнього обчислення однакові. Це пояснюється тим, що розумово відсталим дітям легше дораховувати меншу кількість одиниць до більшого числа. Для пояснення алгоритмів цих обчислень використовуються палички (кубики, арифметична шухляда, абак тощо), з яких утворюється число першого доданка (15) і проводиться його аналіз: 15 - це 1 десяток і 5 одиниць. До даного числа потрібно додати 4 одиниці. Паралельно учні на парті відкладають 1 пучечок (десяток) і 5 паличок (одиниць). Уточнюється другий доданок (4 палички), який додається до розрядних одиниць першого числа. В результаті учні отримують нове число, яке записується на дошці і в зошитах. На початковому етапі навчання обчисленню прикладів даного типу учнів знайомлять з повним записом:   15+4 = 1915 = 10 + 5 5 + 4 = 9 10 + 9=19 При знайомстві школярів з відніманням від двоцифрового числа одноцифрового (наприклад, 15-4) можна використати рахівницю або палички. Учні складають число 15 з 1 пучечка і 5 паличок і з кількості паличок відраховують 4. Міркування проводяться таким чином: "У хлопчика було 15 паличок, тобто 1 десяток і 5 паличок. Я взяв у нього 4 палички (відраховуємо 4 палички від 5). У нього залишились 1 пучечок (тобто 1 десяток) і 1 паличка. Отже, 1 десяток і 1 паличка утворюють число 11". Записується приклад: 15 – 4=11, Учням можна показати і повний запис прийомів: 15 – 4=11 15 = 10 +5 5 – 4 = 1 10+1 = 11 Але повний запис не потрібно проводити після обчислення кожного прикладу. Його доцільно використовувати як унаочнення проведених міркувань. При цьому важливо постійно підкреслювати, що додаються і віднімаються при обчисленні таких прикладів одиниці і кінцевий результат дій у прикладах записується після виконання проміжних результатів. Для закріплення цього можна запропонувати такі прийоми: - підкреслити одиниці в доданках, в зменшуваному і від’ємнику, над якими виконуються обчислювальні операції: 14 + 3=17; 17 – 4=13; - об'єднати одиниці дугою: 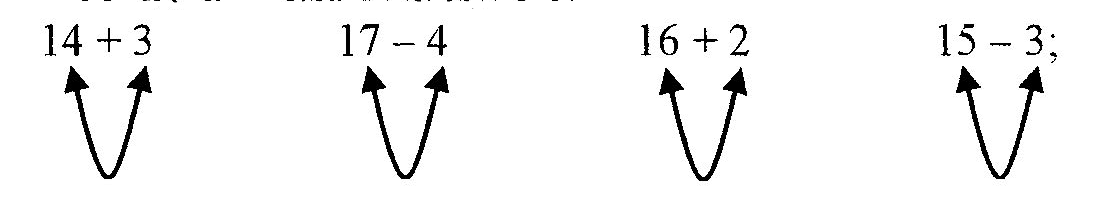 - одиниці і десятки записувати різними кольорами тощо. При виконанні прикладів типу 4+15, 3 + 14 потрібно закріпити з учнями знання переставного закону додавання. На цьому етапі навчання доцільно учням пропонувати обчислення прикладів на співставлення дій першого ступеня в межах 20 з діями в межах 10. 4+3=7 7 – 3=4 3 + 4 = 7 7 – 4 = 3 14 + 3 = 17 17 – 3 = 14 3+14=17 17 – 4=13 б) додавання, коли одиниці в сумі дають кругле число і віднімання від 20 одноцифрового числа: 16 + 4; 18 + 2; 5 + 15; 2 + 18; 20 - 5; 20 - 2. Перед поясненням прийомів виконання прикладів цього типу необхідно повторити з учнями склад чисел першого десятка та таблицю додавання і віднімання в межах 10. Виконання прикладів типу 15 + 5, 18 + 2, 5 + 15,2+18 базується на вже знайомих учням прийомах. Але у них виникає непорозуміння, як при додаванні одиниць у їхньому розряді отримуємо 0. Тому при обчисленні таких прикладів необхідно домагатись від школярів промовляння своїх дій. Наприклад, при обчисленні приклада 16 + 4 учні розмірковують вголос: "Для виконання обчислення прикладу 16 + 4 необхідно число 16 розкласти на 1 десяток і 6 одиниць. (Розкладає 1 пучок і 6 паличок). Потім потрібно виконати дію додавання в розряді одиниць: до 6 паличок додаю 4 палички і отримую 10 паличок, або один десяток паличок. Тепер додаю його до того десятка, який у нас залишився після розкладання числа 16 і в результаті отримуємо 2 десятка, або число 20. Отже, 16 + 4 = 20". При виконанні обчислення прикладів типу 5 + 15,2 + 18 використовується закон перестановки доданків. Повний запис прикладів цього типу матиме такий вигляд: 15+5= 20 15 = 10 + 5 5 + 5 = 10 10 + 10 = 20 При відніманні одноцифрового числа від 20 (20 – 5) учні допоміжної школи допускають досить типову помилку: розклавши 20 на 2 десятки і виконавши віднімання від одного десятка потрібної кількості одиниць, школярі забувають цей залишок додати до десятка, який залишився від розкладання, а тому і отримують помилкову відповідь: 20 – 5 = 5.   Тому доцільно пояснення проводити таким чином: "У числі 20 на місці одиниць стоїть 0, але потрібно відняти 5 одиниць. Для того щоб від 20 відняти 5 необхідно 20 розкласти на 2 десятки. Отже, 20 - це 2 десятки, або 2 пучечки паличок. Один пучечок розкладаємо на десять простих паличок (одиниць) і віднімаємо від них 5 паличок (одиниць). При цьому залишається 5 паличок (одиниць). Оскільки від двох пучечків (від 20) залишився ще 1 пучечок (1 дес.), то додаємо до нього ці 5 паличок (одиниць). Отримуємо результат: 1 дес. і 5 од., або 15. Отже, 20 – 5 = 15". Приклад записується.Надалі учнів треба познайомити з іншими прийомами запису прикладів. Наприклад, при обчисленні приклада 20 – 5 школярам можна запропонувати ставити над десятками крапку, а над нулем - 10. При цьому міркування будуть такими: "Потрібно від 20 відняти 5 одиниць. Знімаємо 1 десяток з розряду десятків і замінюємо його на 10 одиниць, від яких віднімаємо 5 одиниць. У нас залишається 1 дес. і 5 одиниць. Результат записуємо: 20 – 5 = 15". У 2-му класі учням можна показати і повний запис розв'язування прикладів цього виду у двох варіантах: 20–5 = 15 20–5 = 10+10–5 =15 20 = 10+10 10–5 = 5 10–5 = 5 10 + 5 = 15 10 + 5 = 15 в) віднімання від двоцифрового числа, двоцифрового: 16–14, 20–16. Це найбільш складні для розумово відсталих учнів випадки віднімання чисел без переходу через розряд, тому на їх обчислення необхідно звернути особливу увагу. Обчислення можуть проводитись по двох напрямках, з різними підходами. В основі першого варіанту покладено алгоритм розкладання зменшуваного і від'ємника на розрядні одиниці і послідовність віднімання десятків від десятків, одиниць від одиниць: 16–14 = 2 16=10 + 6 14=10 + 4 10–10 = 0 6–4 = 2 Другий прийом - розкладання зменшуваного на десятки і одиниці, а потім послідовне віднімання від зменшуваного спочатку десятків, а потім одиниць: 16–14 = 2 14=10 + 4 16–10 = 6 6–4 = 2 У процесі роботи з розумово відсталими необхідно вибрати один з цих прийомів і добре відпрацювати його з учнями. Самостійно школярі не можуть вибрати, коли доцільно використовувати перший або другий варіант запису приклада. Тому організація одночасного вивчення цих двох прийомів лише заплутає їх. Для закріплення знань доцільно давати завдання на порівняння обчислення прикладів: 15–3= 15–13 = 17–2= 17–12 = Також необхідно використовувати прийом зіставлення одного приклада на додавання з трьома прикладами: одним на додавання (перестановка доданків) і двох на віднімання, порівнюючи компоненти цих прикладів і підкреслюючи їх взаємозв'язок. Наприклад: 12 + 5= і 5+12 = 17–2 = 17–12 = Проводячи обчислення прикладу типу 20 – 15 = учень повинен почати свої міркування у такому плані: "Число 20 – це 2 десятки. Число 15 складається з 1 десятка і 5 одиниць. Спочатку від 2 десятків потрібно відняти 1 десяток. Залишиться 1 десяток. Розкладаємо його на 10 одиниць. Потім від 10 одиниць віднімаємо 5 одиниць, отримуємо 5. Отже, 20 – 15 = 5". 3) Додавання і віднімання з переходом через розряд. У допоміжній школі приклади цього типу вивчаються окремо. Засвоєння алгоритмів обчислення прикладів 5^ межах 20 без переходу через розряд є підготовчим періодом до роботи над прикладами з переходом через десяток. Для ефективнішої організації роботи над даним матеріалом проводиться декілька тематико-пропедевтичних уроків. На них педагог організовує повторення таблиці додавання і    віднімання в межах 10; визначення складу чисел 1-го десятка (для цього доцільно використати таблиці складу чисел усіх можливих варіантів, виготовлені ним у 1-му класі); доповнення чисел до десяти; розкладання двоцифрових чисел на десятки й одиниці; віднімання від 10 і 20 одноцифрових чисел; обчислення прикладів з трьома компонентами, з квадратиками тощо. Крім того, на повторення даного матеріалу доцільно відводити декілька хвилин на початку кожного уроку, присвяченого вивченню вказаної теми.Оскільки школярі вже досить вміло використовують наочність, потрібно пояснення проводити таким чином, щоб вони другий доданок, той, який потрібно розкладати, - обов'язково уявляли, конкретно. Для цього можна використати пальці, рахівниці, палички, арифметичні шухляди тощо. Наочність постійно супроводжує кожен урок математики, адже вона дозволяє у розумово відсталих сформувати усвідомлене розуміння виконуваних обчислень. Успіх в обчисленні прикладів цього типу залежить від знань учнів про склад чисел першого десятка, для перевірки і закріплення яких найкращими завданнями будуть: а) обчислення складних прикладів на дві дії типу:
б) доповнення першого доданка до 10: 5 + + 1 = 7 + + 1 = : 6 + + 1 = 8 + + 1 = в) переведення від повного до скороченого запису прикладів і навпаки: 7 + 2 + 1 = 10 7 + 3 = 10 6 + 4 = 10 6 + 3 + 1 = 10 В.В. Ек вказує, що обґрунтованість можливості такого перетворення математичного виразу, тобто застосування властивості сполучення суми може бути тільки практичним способом (виконання дій з предметами)1. Виконання декількох таких прикладів підказують учням, що замість другого доданку треба писати 2 числа, одне з яких доповнює перше до 10. Однак вивчення прикладів цього типу містить в собі значні труднощі для учнів допоміжної школи. Так, при додаванні вони обумовлені тим, що відразу потрібно актуалізувати раніше отримані знання, упорядкувати їх і послідовно виконати ряд логічних операцій. Наприклад, при обчисленні прикладу 8 + 7 розумово відсталий учень повинен:
Учні відчувають труднощі, по-перше, у розкладанні другого доданка, адже для того, щоб провести це обчислення, потрібно подумки виконати дві операції: визначити, скільки одиниць бракує в першому доданку до десятка; розкласти другий доданок з урахуванням того, скільки одиниць потрібно добавити до десятка; по-друге, в утриманні в пам'яті числа, яке залишилося після доповнення першого доданка до десятка: 10 + 5. При поясненні алгоритму виконання даних обчислень можна застосовувати прийом прилічування або перелічування предметів. Розумово відсталим учням доцільно спочатку проказати, як потрібно розкласти другий доданок на складові. Наприклад: 7 + 5= / \ 3 2, отже, 7 + 3+2 = 12. Для обчислення прикладів на віднімання з переходом через десяток школярі також повинні використовувати усвідомлені дії:
Розумово відсталі учні в основному відчувають труднощі при виконанні третьої і четвертої операцій. Запис даного обчислення можна виконати таким чином:   14 – 6 = / \ 4 2, отже, 14 – 4 – 2 = 8 Засвоєння прийомів розв'язування прикладів цього типу потребує великої підготовчої роботи. Вона повинна бути направлена на повторення:
9)складання прикладів з двома від'ємниками, коли після віднімання першого від'ємника залишається десяток: 14 – – 4 = 6 18 – – 2 = 8 16 – – 3 = 7 Для полегшення вивчення розумово відсталими даного матеріалу спочатку організується обчислення прикладів, у яких перший доданок або зменшуване постійне, а другий доданок або зменшуване збільшується на 1: 9 + 2= 8 + 3= 11 – 2= 12 – 3 = 9 + 3= 8 + 4= 11 – 3= 12 – 4 = 9 + 4= 8 + 5= 11 – 4= 12 – 5 = |