тест по статистике. Гладун И. В_Статистика СКАН. Учебника для использования в учебном процессе образовательных учреждений, реализующих программы спо

• Название: Учебника для использования в учебном процессе образовательных учреждений, реализующих программы спо
• Анкор: тест по статистике
• Дата: 27.09.2022
• Размер: 1.13 Mb.
• Имя файла: Гладун И. В_Статистика СКАН.docx
• Тип: Учебник; #699128
• страница: 31 из 50

Задача 8.5. Произведем сглаживание динамического ряда, пред- ставленного в табл. 8.9, методом трехлетней скользящей средней. Сде- лаем выводы о тенденции развития.

Таблица 8.9

Динамика потребления овощей за месяц на одного члена домохозяйства

Год	2001	2002	2003	2004	2005	2006	2007	2008	2009
Потребление овощей, кг/человек	50	53	60	51	64	81	75	80	90

Решение. Рассчитаем трехлетнюю скользящую среднюю за каждые три года, начиная с 2001 г.:

Y ^Yi ^505360  54,3 кг/человек;

01 03 _t3

Y ^Yi ^536051  54,7 кг/человек;

02  04 _t3

Y ^Yi ^605164  58,3 кг/человек

03  05 _t3

и т.д. Итоги расчетов представим в табл. 8.10.

4. 
   методы анализа основной тенденции в рядах динамики_•143
   

Таблица 8.10

Расчет трехлетней скользящей средней

Год	2001	2002	2003	2004	2005	2006	2007	2008	2009
Потребление овощей, кг/человек	50	53	60	51	64	81	75	80	90
Трехлетняя скользящая средняя	—	54,3	54,7	58,3	65,3	73,3	78,7	81,7	—

Вывод. Произведя сглаживание динамического ряда методом трехлет- ней скользящей средней можно сказать, что потребление овощей за ме- сяц на одного члена домохозяйства имеет четкую тенденцию к росту.

Задача 8.6. Используя данные типовой задачи 8.5:

1. 
   выразим тенденцию потребления овощей с помощью линейного тренда, объяснив содержание параметров уравнения;
   
2. 
   по уравнению тренда рассчитаем величину потребления овощей в 2009 и 2010, 2011 гг.
   

Решение. Исчислим параметры уравнения линейного тренда, пред- ставив результаты расчетов в табл. 8.11:

Y_t= a₀ + a₁t;

a ^Y  ⁶⁰⁴  67,111 шт.;

⁰ n9

a ^Yt ³⁰¹  5,017 шт.;

¹ _t^{2 60}

Y_t= 67,111 + 5,017t.

Таблица 8.11

Расчет параметров уравнения линейного тренда потребления овощей

Год	Y	t	t2	Y t	Yt
2001	50	–4	16	–200	47,043
2002	53	–3	9	–159	52,060
2003	60	–2	4	–120	57,077
2004	51	–1	1	–51	62,094
2005	64	0	0	0	67,111
2006	81	+1	1	81	72,128
2007	75	+2	4	150	77,145
2008	80	+3	9	240	82,162
2009	90	+4	16	360	87,179
Итого:	604	0	60	301	Х

144_•глава 8. ряды динамики

Вывод. В 2001—2009 годах средний объем потребления овощей за месяц на одного члена домохозяйства составляет 67,111 кг. Потреб- ление овощей ежегодно увеличивается в среднем на 5,017 кг.

Если допустить, что выявленная тенденция сохранится и в буду- щем, то объем потребления овощей за месяц на одного члена домохо- зяйства будет составлять в 2010 г. 92,196 кг/человек:

Y₂₀₁₀ = 67,111 + 5,017  5 = 67,111 + 25,085 = 92,196 кг/человек.

В 2011 году — 97,213 кг/человек:

Y₂₀₁₁ = 67,111 + 5,017  6 = 67,111 + 30, 102 = 97,213 кг/человек.
Задача 8.7. Рассчитаем и сравним прогнозные значения уровня потребления овощей за месяц на одного члена домохозяйства в 2010, 2011 гг., используя различные методы экстраполяции (перенесения су- ществующей тенденции в будущее):

1. 
   по уравнению линейного тренда;
   
2. 
   на базе среднего абсолютного прироста;
   
3. 
   на базе среднего темпа роста.
   

Решение.

1. 
   Рассчитаем уровень потребления овощей за месяц на одного члена домохозяйства в 2010 г. набазесреднегоабсолютногоприроста по формуле
   

Y_it Y_i t.

Для этого рассчитаем средний абсолютный прирост потребления овощей по данным динамического ряда по формуле

  ^YiYit ^{Y2009Y2001}  ^90  ⁴⁰  5 кг/человек.

t8 8 8

Вывод. В 2001—2009 годах потребление овощей за месяц на одного члена домохозяйства в среднем ежегодно увеличивалось на 5 кг/че- ловек.

Если предположить, что выявленная средняя абсолютная скорость роста сохранится и в будущем, то потребление овощей за месяц на од- ного члена домохозяйства будет составлять в 2010 г.:

Y₂₀₀₉₊₁ = Y₂₀₁₀ = Y₂₀₀₉ + 5  1 = 90 + 5 = 95 кг/человек.

В 2011 году:

Y₂₀₀₉₊₂ = Y₂₀₁₁ = Y₂₀₀₉ + 5  2 = 90 + 10 = 100 кг/человек.

4. 
   статистическое изучение сезонных колебаний_•145
   

2. 
   
   t
   Рассчитаем уровень потребления овощей за месяц на одного члена домохозяйства в 2010 г. на базе среднего темпа роста по формуле
   

Y_t+1 = Y_i ^Кр.

Для этого рассчитаем средний коэффициент роста потребления овощей:




Кр      1,076.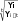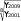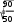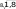
Вывод. В 2001—2009 годах потребление овощей в среднем ежегодно увеличивалось в 1,076 раз.

Если допустить, что выявленная средняя относительная скорость роста сохранится и в будущем, то потребление овощей будет состав- лять в 2010 г.:

1
^Y2009+1 ^{= Y}2010 ^{= Y}2009 ^{ Кр}

В 2011 году:

= 90  1,076 = 96,84 кг/человек.

2009+2 2011 2009
Y= Y= Y ^Кр2 = 90  1,076² = 90  1,1578 =

= 104,20 кг/человек.

Как видно из табл. 8.12, прогнозные значения, полученные различ- ными методами, отличаются друг от друга.

Таблица 8.12

Прогноз уровня потребления овощей в месяц на одного члена домохозяйства

Год	Прогноз на основе
	тренда	среднего абсолютного прироста	среднего темпа роста
2010	92,196	95	96,84
2011	97,213	100	104,20

Точность прогноза определяется тем, насколько правильно сформу- лирована гипотеза о закономерности развития прогнозируемого явления.