Логика. Учебное пособие (2018) (1). Учебное пособие Уфа 2018 удк 16 ббк 87. 4 И851 Рекомендовано к опубликованию
 Скачать 1.2 Mb. Скачать 1.2 Mb.
|
|
Глава 5. Умозаключение Суждения находятся в определенном отношении друг к другу, зависят одно от другого. Это служит логическим основанием для выведения нового суждения из других. Эта операция в логике называется умозаключением. Большую часть знаний человек получает именно с помощью умозаключений. Эти знания называются выводными, или опосредствованными (в отличие от непосредственных знаний, получаемых через органы чувств). Умозаключение является самой сложной формой мыслительной деятельности. Оно состоит из суждений, а последние – из понятий. По этой причине исследование умозаключения и продуктивная работа с этой формой мысли предполагает знание особенностей и норм работы с понятиями и суждениями. При соблюдении этого условия усвоение теории умозаключения не представляет особой трудности. Вот что писал по этому поводу Дж. С. Милль: «Когда я принимаю в соображение как проста теория умозаключения, какого небольшого времени достаточно для приобретения полного знания его принципов и правил и даже значительной опытности в их применении, я не нахожу никакого извинения для тех, кто, желая заниматься с успехом каким-нибудь умственным трудом, упускает это изучение». 5.1. Общая характеристика умозаключений. Непосредственные умозаключения и способы их образования Можно дать следующее определение: умозаключение – это форма мышления, посредством которой из одного или нескольких суждений выводится новое суждение. Умозаключение состоит из посылок и заключения. Посылки – это суждения, из которых делается вывод. Заключение – это суждение, полученное в результате вывода. Выводом называют способ связи посылок и заключения между собой.    Разберем состав умозаключения на следующем примере: Все юристы должны знать логику. Синицын – юрист. Синицын должен знать логику. Суждения «Все юристы должны знать логику» и «Синицын – юрист» являются в этом умозаключении посылками, а суждение «Синицын должен знать логику» – заключением. Черта под посылками означает переход от посылок к заключению и читается как «следовательно». Если умозаключение имеет одну посылку, то его называют непосредственным умозаключением, или умозаключением в несобственном смысле. Например: Все работники отдела прошли медицинский осмотр. Некоторые из прошедших медицинский осмотр являются работниками отдела. Видно, что из информации, выраженной в первом предложении этого рассуждения, выводится другая информация, выраженная через другое предложение. Если вывод делается из двух и более посылок, то умозаключение называют опосредованным. Например: Все работники правового отдела прошли медицинский осмотр. Кожемякин является работником правового отдела. Кожемякин прошел медицинский осмотр. Большинство умозаключений относится к классу опосредствованных. Однако люди нередко прибегают к выводам в форме непосредственных умозаключений, которые могут быть полезны при составлении документов или в других случаях, когда какую-то мысль нужно выразить в иной форме, более удобной для изложения в данном конкретном случае. Непосредственные умозаключения образуются путем следующих способов: превращения, обращения, противопоставления предикату и по логическому квадрату. Виды непосредственных умозаключений     Превращение Обращение Противопоставление предикату Вывод по логическому квадрату Превращение – это логический прием, связанный с изменением связки и предиката посылки на противоположные. Например: Все преступники – правонарушители. Ни один преступник не является не правонарушителем. Общая логическая схема превращений основных видов суждений такова: А Е; Е А; I O; O I. Превращение
Таким образом, с помощью этого способа утвердительные суждения превращаются в отрицательные, а отрицательные – в утвердительные. Обращение – это преобразование посылки, в результате которого ее субъект становится предикатом, а предикат – субъектом заключения. Например: Некоторые курсанты первого курса сдали экзамен по логике. Некоторые, сдавшие экзамен по логике, – курсанты первого курса. В общем виде основные обращения можно записать следующим образом: A I; E E; I I; A A. Частноотрицательные суждения (О) не обращаются. Обращение
Противопоставление предикату – это логическая операция, в процессе которой субъектом заключения становится отрицаемый предикат посылки, в качестве предиката берется субъект посылки, связка посылки отрицается и в таком виде становится связкой заключения. Например: Все студенты нашего факультета изучают логику. Все, не изучающие логику, не являются студентами нашего факультета. Общая логическая схема противопоставлений такова: А Е; Е I; О I. Частноутвердительные суждения (I) не допускают противопоставления предикату. Противопоставление предикату
Умозаключение по логическому квадрату – это логическая операция преобразования категорических суждений с учетом истинности между ними (по логическому квадрату).    A E A EI O Как мы уже знаем, по логическому квадрату возникает четыре типа отношений между суждениями. Рассмотрим каждое из них в отдельности. Выводы из отношения противоречия. Это отношение возникает между суждениями А и О, а также между Е и I. Известно, что, если суждение «Во всех государствах существуют налоги» (А) истинно, то суждение «В некоторых государствах нет налогов» (О) будет ложным. И, наоборот, из ложности суждения «Все люди читают газеты» (А) следует истинность суждения «Некоторые люди не читают газет» (О). То же самое возможно между суждениями Е и I. В общем виде можно изобразить выводы из этого отношения следующими формулами: А(и) О(л); А(л) О(и); Е(и) I(л); Е(л) I(и) О(и) А(л); О(л) А(и); I(и) Е(л); I(л) Е(и) Выводы из отношения контрарности (противоположности). Это отношение возникает между суждениями А и Е. Из истинности одного из этих суждений всегда следует ложность другого. Например, от истинности суждения «Все растения – организмы» (А) приходим к ложности суждения «Ни одно растение не есть организм» (Е). Но из ложности суждения «Все преступники – честные люди» (А) мы не можем дать однозначного ответа относительно суждения «Ни один преступник не является честным человеком» (Е). Оно может быть как ложным, так и истинным, т. е. оно неопределенно. Поэтому обоснованные выводы из этого отношения можно делать лишь по двум схемам: А (и) Е (л); Е (и) А (л) Выводы из отношения субконтрарности (частичной совместимости). Это отношение, как известно, возникает между суждениями I и О. Здесь также возможны лишь два случая образования умозаключений. От ложности одного из этих суждений мы приходим к истинности второго. Например, если суждение «Некоторые преступники не признают своей вины» (О) ложное, то суждение «Некоторые преступники признают свою вину» (I) – истинное. При истинности первого суждения в данном отношении второе будет неопределенным: то ли истинным, то ли ложным. Схематически выводы из этого отношения выглядят так: I (л) О (и); О (л) I (и) Выводы из отношения подчинения. Эти выводы можно разделить на две группы: а) умозаключение от подчиняющего к подчиненному (А – I; Е – О); б) умозаключение от подчиненного к подчиняющему (I – А; О – Е). Умозаключение от подчиняющего к подчиненному можно образовывать только исходя из истинности общих суждений. От истинности суждения «Все люди подвержены заблуждениям» (А) мы приходим к истинности суждения «Некоторые люди подвержены заблуждениям» (I). От ложности же общих суждений мы приходим к неопределенности частных суждений. Схемы этих выводов выглядят следующим образом: А (и) I (и); Е (и) О (и) Умозаключение от подчиненного к подчиняющему можно образовывать лишь исходя из ложности частных суждений. Так, если суждение «Некоторые юридические законы не обязательны для исполнения» (О) ложное, то и суждение «Все юридические законы не обязательны для исполнения» (Е) тоже будет ложным. Из истинности же частных суждений мы не можем дать однозначного ответа относительно общих суждений. Схемы вывода здесь таковы: I (л) А (л); (л) Е (л) Рассмотрим вышесказанное на примерах. Определите, каким способом образованы следующие непосредственные умозаключения. Пример 1. Все пословицы – краткие изречения. Следовательно, некоторые краткие изречения – пословицы. Решение: Это обращение, так как субъект посылки «пословицы» становится предикатом, а предикат посылки «краткие изречения» – субъектом заключения. Пример 2. Все прекрасное есть ценность. Значит, ни одно прекрасное не является неценным. Решение: Это операция превращения, так как связка и предикат посылки в заключении изменены на противоположные. Пример 3. Все курсанты нашего института принимали присягу. Ни один, не принимавший присягу, не является курсантом нашего института. Решение: Это умозаключение образовано путем противопоставления предикату. Субъектом заключения становится отрицаемый предикат посылки «принимавший присягу», предикатом заключения становится в неизменном виде субъект посылки «курсанты нашего института», связка посылки меняется на противоположную в заключении. Пример 4. Неверно, что все преступники – честные люди, значит, некоторые преступники не являются честными людьми. Решение: Умозаключение построено по логическому квадрату. Между этими суждениями возникает отношение противоречия, т. к. первое суждение «Все преступники – честные люди» является общеутвердительным (А), а второе – «Некоторые преступники не являются честными людьми» – частноотрицательным (О). Из ложности суждения А следует истинность суждения О. 5.2. Дедуктивные умозаключения Как было отмечено, если умозаключение имеет более одной посылки, то его называют опосредованным (опосредствованным). Такие умозаключения делятся на дедуктивные, индуктивные и традуктивные (по аналогии). Дедуктивное (от лат. «deduction» – «выведение») умозаключение представляет собой движение мысли от общего к частному. Такое движение приведет к истинному знанию при соблюдении двух условий: 1) посылки являются истинными; 2) соблюдаются правила вывода, о которых речь пойдет ниже. Из всего вышеизложенного можно дать следующее определение: дедуктивным называется умозаключение, в котором переход от общего знания к частному является логически необходимым. Например: Все растения – организмы. Розы – растения. Розы – организмы. Существуют различные виды дедуктивных умозаключений. Рассмотрим такие их виды, как простой категорический силлогизм, условно-категорическое умозаключение, разделительно-категорическое умозаключение, условно-разделительное умозаключение, а также сокращенные силлогизмы. Простой категорический силлогизм (ПКС) Простой категорический силлогизм – это дедуктивное умозаключение, посылки и вывод которого являются категорическими суждениями. Сам термин «силлогизм» (от греч. «syllogismos» – сосчитывание) был введен еще Аристотелем, который теорию умозаключений называл силлогистикой. В настоящее время этот термин применяют как в узком смысле, обозначая им простое категорическое умозаключение, так и в широком, обозначая любое дедуктивное умозаключение. Приведем следующий пример простого категорического силлогизма: Все курсанты третьего курса прошли медицинский осмотр. Вахитов – курсант третьего курса. Вахитов прошел медицинский осмотр. Видно, что здесь мысль идет от общего знания к единичному, и все три суждения, входящие в состав силлогизма, являются категорическими суждениями. Вывод в простом категорическом силлогизме основывается на так называемой аксиоме силлогизма: все, что утверждается или отрицается относительно предметов всего класса, утверждается или отрицается и относительно каждого отдельного предмета этого класса. Простой категорический силлогизм включает в себя три термина. Термины – это понятия, из которых состоит данное умозаключение. Оно имеет субъект (меньший термин), предикат (больший термин) и средний термин. Субъект (меньший термин) – это то, о чем идет речь в заключении, т. е. субъект заключения. Этот термин обозначается латинской буквой S. В приведенном выше примере речь в заключении идет о Вахитове. Следовательно, субъект данного силлогизма – Вахитов. Предикат (больший термин) – это признак, который приписывается или не приписывается субъекту в заключении, т. е. предикат заключения. Он обозначается латинской буквой Р. В нашем примере предикатом является словосочетание «прошел медицинский осмотр». Субъект и предикат вместе называются крайними терминами силлогизма. Средний термин – это понятие, обязательно присутствующее в обеих посылках, но отсутствующее в заключении. Обозначается этот термин латинской буквой М. В приведенном примере средним термином является понятие «курсант третьего курса». Такие названия терминов вытекают из отношения между их объемами. Если изобразить при помощи кругов Эйлера первую посылку приведенного выше умозаключения как отношение между средним термином «курсант третьего курса» и большим термином «прошедшие медицинский осмотр», то получим следующую картину:   Теперь изобразим в круговых схемах вторую посылку, где говорится, что Вахитов (S) является курсантом третьего курса (М):   Но если понятие М входит полностью в понятие P, a S полностью входит в М, то отсюда с необходимостью следует, что S входит в Р. Такое утверждение и содержится в заключении, которое при символическом изображении выглядит следующим образом:   Из приведенных круговых схем видно, что субъект имеет самый меньший объем. Поэтому его называют меньшим термином. Предикат же имеет самый больший объем. Поэтому его называют большим термином. А средний термин в соответствии со своим названием располагается между указанными крайними терминами.    Посылку, содержащую субъект, в логике принято называть меньшей посылкой, а посылку, содержащую предикат, большей посылкой. В приведенном примере посылка «Все курсанты третьего курса прошли медицинский осмотр» является большей, а «Вахитов – курсант третьего курса» – меньшей посылкой. Выше уже было сказано, что для получения истинного знания в дедуктивных умозаключениях должны быть истинные посылки и соблюдаться ряд правил. В простом категорическом силлогизме существуют общие правила и правила фигур. В свою очередь общие правила делятся на правила посылок и правила терминов. а) Правила посылок 1. Из двух отрицательных посылок заключение не следует. Например: Растения не могут мыслить. Камень не растение. ? Видно, что здесь следует заключение «Камень может мыслить», которое является ложным суждением. Если изобразить данное умозаключение в виде отношений между объемами его субъекта «камень», предиката «может мыслить» и среднего термина «растение», получим следующую картину: Первая посылка Вторая посылка     Из этих двух схем какого-то однозначного вывода об отношении между субъектом и предикатом не следует. 2. Из двух частных посылок заключение с необходимостью не следует. Например: Некоторые курсанты нашего института – спортсмены. Некоторые спортсмены живут в Африке. ? Здесь следует заключение «Некоторые курсанты нашего института живут в Африке», которое не обязательно является истинным или ложным суждением (оно неопределенно). Изобразим отношения между терминами данного умозаключения в виде круговых схем. Субъектом умозаключения является понятие «курсанты», предикатом – «живущие в Африке», средним термином – «спортсмены». В таком случае первые две посылки будут иметь такой вид: Первая посылка Вторая посылка 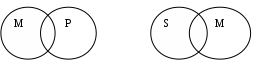 Но из такого отношения между указанными терминами возможны следующие выводы относительно S и Р: 1) S не входит в Р; 2) S частично входит в Р; 3) S полностью входит в Р. Если изобразить эти три случая в круговых схемах, то получим: Первый случай Второй случай Третий случай 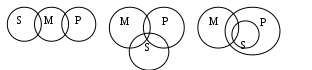 Таким образом, видно, что из двух частных посылок однозначный вывод сделать невозможно. 3. Если одна посылка отрицательная, то заключение должно быть отрицательным. Например: Все курсанты юридического института принимали присягу. Кириллов не принимал присягу. Кириллов не является курсантом юридического института. Проверим обоснованность заключения при помощи круговых схем. Субъектом данного умозаключения является понятие «Кириллов», предикатом – «курсант юридического института», средним термином – «принимать присягу». Изобразим сначала через круговые схемы первую и вторую посылки: Первая посылка Вторая посылка   Из данных схем вытекает, что если Р полностью входит в М, a S не входит в М, то S не может входить в Р. Следовательно, заключение в этом силлогизме не может быть утвердительным. 4. Если одна посылка частная, то заключение должно быть частным. Например: Все преступники – правонарушители. Некоторые водители – преступники. Некоторые водители – правонарушители. Очевидно, что общее заключение «Все водители – правонарушители» было бы в данном случае ошибочным. б) Правила терминов 1. В категорическом силлогизме должно быть только три термина. Ошибка, возникающая при нарушении этого правила, носит название «учетверение термина». Например: Клетка – составная часть живого организма. Эта тетрадь в клетку. ? Из этих двух посылок следует вывод «Тетрадь – живой организм», который является ошибочным. Ошибка возникает, потому что средний термин «клетка» в первой посылке выступает в одном значении (часть живых организмов), а во второй посылке – в другом (вид тетради). Поэтому вместо одного имеется два средних термина, и всего в умозаключении их становится четыре. Отсюда и название ошибки, возникающей при нарушении данного правила. По сути, данное правило является своеобразным выражением требования закона тождества, который запрещает в рамках одного рассуждения применять одно и то же слово в разных значениях. 2. Средний термин должен быть распределен по крайней мере в одной из посылок. Рассмотрим это правило на классическом для логики примере: Все кошки смертны. Сократ смертен. Сократ – кошка. Субъектом этого умозаключения является «Сократ», предикатом – «кошка», средний термин – «смертен». Из темы «Суждение» известно, что термин считается распределенным, если его объем полностью входит в объем другого термина или полностью исключается из него. Посмотрим, распределен ли средний термин в первой посылке. Для этого изобразим отношение между предикатом и средним термином в виде кругов Эйлера:   Из данной схемы видно, что средний термин в первой посылке не распределен. Теперь изобразим отношение между субъектом и средним термином во второй посылке:  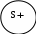 Здесь также средний термин не распределен. Таким образом, данное правило не выполняется и умозаключение является неверным. 3. Если термин распределен в заключении, то он должен быть распределен и в посылке. Рассмотрим это правило на примере его нарушения: Все курсанты должны знать устав. Офицеры не являются курсантами. Офицеры не должны знать устав. Ошибочность данного заключения доказывается следующим образом. Определяем субъект, предикат и средний термин. Субъектом данного умозаключения является понятие «офицеры», предикатом – «люди, которые должны знать устав», средним термином – «курсанты». Теперь нужно изобразить заключение в виде отношения между субъектом и предикатом. Получаем следующую схему: 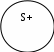  По этой схеме видно, что в заключении оба термина (субъект и предикат) распределены. Следовательно, они должны быть распределены и в посылках (согласно правилу). Рассмотрим первую посылку. Отношение между средним термином «курсанты» и предикатом «люди, которые должны знать устав» в кругах Эйлера выглядит следующим образом:  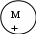 Видно, что предикат в первой посылке не распределен, что является нарушением правила. Даже независимо от того, распределен ли субъект во второй посылке, данное умозаключение является необоснованным. Ошибку, связанную с нарушением этого правила в логике принято называть «незаконное расширение термина». Как уже было изложено выше, кроме общих правил простого категорического силлогизма существуют правила фигур. Фигуры – это схемы, изображающие различные формы соединения в посылках субъекта и предиката со средним термином. Первая фигура Эта схема отличается тем, что в ее большей посылке средний термин стоит впереди предиката, а в меньшей – после субъекта. 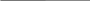  М Р М Р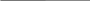 S М S МЛиния МР означает первую, SМ – вторую посылку, а линия ММ означает связь между этими двумя посылками (поскольку именно средний термин является связующим звеном между суждениями, являющимися посылками умозаключения). Например: Все адвокаты (М) – юристы (Р). Иванов (S) – адвокат (M). Иванов (S) – юрист (P). Если мысль построена по этой схеме, то она должна подчиняться двум правилам: 1. Посылка, содержащая предикат (большая посылка), должна быть общим суждением. 2. Посылка, содержащая субъект (меньшая посылка), должна быть утвердительным суждением. Проверим по правилам приведенный выше пример. Большая посылка «Все адвокаты – юристы» является общим суждением, а меньшая посылка «Иванов – адвокат» – утвердительное суждение. Значит, оба правила выполняются, и этот силлогизм состоятелен. Вторая фигура  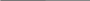 Р М Р М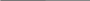 S М S МВидно, что здесь средний термин стоит после предиката в большей посылке и после субъекта в меньшей. Например: Всякое мошенничество (Р) есть преступление (М). Данное деяние (S) не является преступлением (M). Данное деяние (S) не есть мошенничество (Р). Мысль, построенная по этой схеме, должна отвечать двум требованиям: 1. Посылка, содержащая предикат, должна быть общим суждением. 2. Одна из посылок должна быть отрицательным суждением. Проверим, как выполняются правила в нашем примере. Большая посылка «Всякое мошенничество есть преступление» – общее суждение, т. е. первое правило соблюдается. Отрицательная посылка – вторая «Данное деяние не является преступлением». Следовательно, второе правило выполнено, и силлогизм считается состоятельным. Подтверждается это решение и при проверке правильности силлогизма через круговые схемы. Так, если «данное деяние» обозначить через S, «мошенничество» – Р, «преступление» – через М, то в кругах Эйлера данное умозаключение будет выглядеть так:    Очевидно, что если S не входит в М, то S не может входить и в Р. Третья фигура 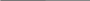  М Р М Р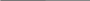 М S М SВ этой фигуре средний термин стоит в обеих посылках в начале – впереди крайних терминов (предиката и субъекта). Например: Все сотрудники полиции (М) имеют специальное звание (Р). Некоторые сотрудники полиции (М) – женщины (S). Некоторые женщины (S) имеют специальное звание (Р). Эта фигура имеет также два правила: 1. Посылка, содержащая субъект, должна быть утвердительной. 2. Заключение должно быть частным или единичным суждением. Проверим по этим нормам приведенный пример. Меньшая посылка «Некоторые сотрудники полиции – женщины» является утвердительным суждением, что говорит о выполнении первого правила. Заключение «Некоторые женщины имеют специальное звание» – частное суждение. Второе правило тоже выполняется. Следовательно, данное умозаключение является обоснованным. Проверим его и при помощи круговых схем. Субъектом данного силлогизма является понятие «женщины», предикатом – «имеющие специальное звание», средним термином – «сотрудники милиции». Эти понятия между собой будут находиться в следующих отношениях:    Видно, если S частично входит в объем М, то с необходимостью частично входит и в объем Р. Имеется также и четвертая фигура простого категорического силлогизма, но она является искусственным построением и практической ценности не имеет. Посылками силлогизма могут быть суждения, различные по качеству и количеству: общеутвердительные (А), общеотрицательные (Е), частноутвердительные (I) и частноотрицательные (О). На основе их различного сочетания выделяют модусы простого категорического силлогизма. Модусы простого категорического силлогизма – это его разновидности, отличающиеся друг от друга качественной и количественной характеристикой входящих в них посылок и заключения. Для того чтобы вывод считать достоверным, силлогизм должен соответствовать правильным модусам фигуры: 1-я фигура: ААА, ЕАЕ, АII, EIO 2-я фигура: EAE, AEE, EIO, AOO 3-я фигура: AAI, IAI, AII, EAO, OAO, EIO В каждом модусе первая буква выражает вид суждения (по объединенной классификации), выражающего большую посылку, вторая буква – меньшую, а третья – заключение. Все другие модусы формально возможны, но они не ведут к получению достоверного знания. Таким образом, для того чтобы проверить правильность категорического силлогизма при помощи его фигур, необходимо найти субъект, предикат и средний термин умозаключения и построить из них фигуру. Далее по правилам соответствующей фигуры нужно выяснить обоснованность заключения. Разберем следующий пример: Банда Шварца является общественной организацией, так как общественная организация является добровольным объединением, а банда Шварца – добровольное объединение. Решение: Выполнение данного задания необходимо проводить по следующему алгоритму: 1. В приведенном примере сначала необходимо найти заключение (заключение – это суждение, полученное в результате вывода). Заключение отвечает на вопрос: «Что обосновывается?». В этом силлогизме заключение приведено раньше посылок. Это легко обнаружить, если поставить вопрос: «А что же обосновывается в приведенном умозаключении?». А обосновывается здесь то, что банда Шварца является общественной организацией. Заключение: Банда Шварца является общественной организацией. 2. В заключении необходимо выделить субъект (S – это логическое подлежащее заключения) и предикат (Р – то, что утверждается или отрицается в заключении по отношению к субъекту) ПКС. В данном примере: S – банда Шварца. Р – общественная организация. 3. Найти средний термин (М – входит в содержание обеих посылок, но отсутствует в заключении). В данном примере: М – добровольное объединение. 4. Найти большую посылку (содержит предикат и средний термин). В данном примере: Р М Общественная организация является добровольным объединением. 5. Найти меньшую посылку (содержит субъект и средний термин). В данном примере: S М Банда Шварца – добровольное объединение. 6. Составить фигуру (верхняя линия выражает структуру большей посылки, нижняя линия выражает структуру меньшей посылки). В данном примере большая посылка имеет структуру Р – М, а меньшая посылка S – М.  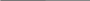 Р М Р М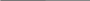 S М S МТаким образом, умозаключение построено по второй фигуре. 7. Необходимо проверить правила получившейся фигуры. Проверяем правила второй фигуры. Первое правило соблюдено (большая посылка является общим суждением). Второе правило не соблюдено. Согласно этому правилу одна из посылок должна быть отрицательным суждением. Но в рассматриваемом умозаключении обе посылки утвердительные. Значит, данное умозаключение построено с нарушением одной из логических норм, и его заключение не обосновано. |
