Логика. Учебное пособие (2018) (1). Учебное пособие Уфа 2018 удк 16 ббк 87. 4 И851 Рекомендовано к опубликованию
 Скачать 1.2 Mb. Скачать 1.2 Mb.
|
|
4.3. Распределенность терминов в суждениях В формальной логике важное значение придается установлению отношения между объемами терминов суждения – субъекта и предиката. Термин называется распределенным, если его объем полностью входит в объем другого термина или полностью исключается из него. По сути, здесь речь идет об определении отношения между понятиями, выражающими субъект и предикат. Если рассмотреть распределенность терминов в суждениях, выделяемых объединенной классификацией, то получим следующую картину. В общеутвердительных суждениях субъект всегда распределен, а предикат, как правило, не распределен (он бывает распределенным только в случаях, когда субъект и предикат являются равнозначными понятиями). Например: «Декабрь в северном полушарии (S) является зимним месяцем (Р)», «Декабрь в северном полушарии (S) является первым зимним месяцем (Р)». Во втором случае и субъект, и предикат являются распределенными. Если изобразить отношения между терминами в кругах Эйлера, получим следующую картину. Первое суждение Второе суждение  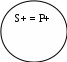  Знак «–» означает, что термин не распределен, знак «+» означает, что термин распределен. В общеотрицательных суждениях оба термина всегда распределены, так как их объемы полностью исключают друг друга. Выразим субъект и предикат суждения «Ни один крокодил (S) не является млекопитающим (Р)» в виде круговых схем. 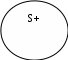  Видно, что оба термина отвечают требованию распределенности. В частноутвердительных суждениях оба термина, как правило, не распределены, так как находятся в отношении пересечения «Некоторые студенты (S) занимаются спортом (Р)». И субъект, и предикат в этом случае берутся не в полном объеме. По этой причине оба термина не распределены. Но в редких случаях в частноутвердительных суждениях наблюдается подчинение предиката субъекту. Например: «Некоторые врачи (S) являются терапевтами (P)». В последнем примере предикат распределен – он полностью входит в объем субъекта (очевидно, что понятие «терапевты» (предикат) полностью входит в объем понятия «врач» (субъект)». В кругах Эйлера эти два случая можно изобразить так: Первый пример Второй пример     В частноотрицательных суждениях субъект не распределен, а предикат – распределен. Например: «Некоторые картины не подлежат продаже». Здесь субъект берется не в полном объеме (только некоторые картины), а предикат – в полном, так как мы из его объема полностью исключаем субъект (те картины, о которых идет речь, не могут войти в класс вещей, подлежащих продаже). В кругах Эйлера это будет выглядеть так:  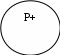 Все изложенное о распределенности терминов можно изобразить в виде таблицы 4.2. Таблица 4.2
Рассмотрим сказанное выше на примерах. Пример 1. Материализм есть философское течение. Решение: Субъект здесь полностью входит в объем предиката. Следовательно, субъект распределен, а предикат нет. Пример 2. Часть юристов имеют среднее образование. Решение: Объемы обоих терминов в этом суждении берутся не в полном объеме (субъект и предикат находятся в отношении пересечения). Следовательно, оба термина не распределены. 4.4. Отношения между простыми суждениями. Логический квадрат И в практической, и в теоретической деятельности человеку постоянно приходится сравнивать различные суждения и делать на этом основании определенные выводы. Есть суждения, которые можно сравнивать, но есть и такие, которые несравнимы. Например, суждения «В БГУ закончились вступительные экзамены» и «Понятие есть форма мысли» являются несравнимыми. Сравнимыми являются суждения, имеющие одинаковые термины (субъект и предикат) и различающиеся лишь по качеству и количеству. Сравнимые суждения в свою очередь делятся на совместимые и несовместимые. Совместимыми являются суждения, которые могут быть одновременно истинными. Например: «Некоторые люди знают физику», «Некоторые люди не знают физику». Эти суждения, отличающиеся лишь по качеству, оба истинны. Очевидно, что при истинности суждения «Все автомобили марки «Камаз» работают на дизельном топливе», суждение «Некоторые автомобили «Камаз» работают на дизельном топливе» тоже будет истинным. Первый вид отношения, который имеет место между частными суждениями, называют отношением частичной совместимости, или субконтрарности. Такие суждения могут быть одновременно истинными, но не могут быть одновременно ложными. Для такого отношения характерны следующие зависимости: 1) при истинности одного из суждений другое может быть как истинным, так и ложным, т. е. неопределенно; 2) при ложности одного из суждений другое обязательно будет истинным. Второй вид отношения, который имеет место между общим и частным суждениями, отличающимися лишь по количеству, называют отношением подчинения. При истинности общего суждения частное суждение всегда истинно, но не наоборот. Для такого отношения характерны следующие зависимости: 1) при истинности общего суждения частное всегда будет истинным; 2) при ложности общего суждения частное может быть как истинным, так и ложным, т. е. неопределенно; 3) при истинности частного суждения общее может быть как истинным, так и ложным, т. е. неопределенно; 4) при ложности частного суждения общее всегда будет ложным. Например, при истинности частного суждения «Некоторые курсанты, живущие в комнате 245, родились в 1991 году» общее суждение «Все курсанты, живущие в комнате 245, родились в 1991 году» может быть и ложным, и истинным. Другой пример, при ложности общего суждения «Все часы, находящиеся в этой аудитории, идут точно» суждение «Некоторые часы, находящиеся в этой аудитории, идут точно» может быть истинным, но может быть и ложным (если все часы будут идти неточно). Несовместимыми являются суждения, которые одновременно не могут быть истинными. Такие суждения могут находиться в отношении контрадикторности (противоречия) и контрарности (противоположности). В отношении контрадикторности находятся суждения, разные как по количеству, так и качеству. Они не могут быть ни одновременно истинными, ни одновременно ложными. В таком отношении, например, находятся следующие суждения: «Все убийства совершаются умышленно» и «Некоторые убийства не совершаются умышленно». Для такого отношения характерны следующие зависимости: 1) при истинности одного суждения другое всегда будет ложным; 2) при ложности одного суждения другое всегда будет истинным. В отношении контрарности находятся общие суждения, имеющие разное качество (общеутвердительное и общеотрицательное). Эти суждения не могут быть одновременно истинными, но могут быть одновременно ложными. Например: «Все политики – лгуны» и «Ни один политик не является лгуном». Для этого вида отношения характерно следующее: 1) при истинности одного суждения другое всегда будет ложным; 2) при ложности одного суждения другое может быть как истинным, так и ложным, т. е. неопределенно. Схема 4.2 Суждения   Несравнимые Сравнимые 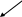 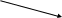 Совместимые Несовместимые   Отношение подчинения Отношение контрарности 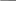 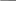 Отношение субконтрарности Отношение контрадикторности   Отношения между простыми суждениями еще в XI веке византийский ученый Михаил Псёлл схематически выразил при помощи фигуры, известной под названием «логический квадрат».    A E A EI O В этой фигуре каждая линия, соединяющая виды суждений, выражает какое-либо отношение между ними. Так, линия АЕ выражает отношение контрарности, линии АI и ЕО – отношение подчинения, линии АО и ЕI – отношение контрадикторности, а линия IO – отношение субконтрарности. Все изложенное о логическом квадрате представлено в таблице 4.3. Таблица 4.3
Здесь «И» означает истинность суждения, «Л» – его ложность, а «Н» – неопределенность1. Благодаря указанным логическим закономерностям, существующим между суждениями, их можно оценивать с позиций истинности, что важно в теории умозаключений. Определение истинности или ложности суждения, исходя из истинности или ложности другого сравнимого с ним суждения, можно проводить по одной из следующих методик. Первый метод. Сначала необходимо определить вид каждого суждения по объединенной классификации, затем определить вид отношения между суждениями, и потом определить истинность или ложность второго суждения, исходя из истинности или ложности первого суждения с учетом характеристик данного вида отношений между суждениями. Второй метод. Сначала определить вид каждого суждения по объединенной классификации, затем подставить полученные данные в таблицу. В левой графе найти суждение, истинность или ложность которого установлена, провести линию до пересечения со вторым видом суждения. Рассмотрим сказанное выше на примерах. Пример 1. Определить истинность второго суждения, приняв первое за истинное: Металлы электропроводны. Некоторые металлы не электропроводны. Решение: Первое суждение общеутвердительное (А), второе – частноотрицательное (О). Тогда между ними существует отношение противоречия, которое предполагает, что если первое суждение истинно, то второе – ложно. Пример 2. Определить истинность второго суждения, приняв первое за ложное: Все работники нашего отдела имеют высшее образование. Ни один работник нашего отдела не имеет высшего образования. Решение: Для решения сначала нужно определить вид каждого суждения этой пары по объединенной классификации. Видно, что первое суждение – общеутвердительное (А), второе – общеотрицательное (Е). По условиям задачи, первое суждение (А) ложно. Подставим полученные данные в таблицу. Если (А) ложно, то (Е) – неопределенно, т. е. может быть как истинным (если ни один работник нашего отдела не имеет высшего образования), так и ложным (если некоторые из работников нашего отдела имеют высшее образование, а некоторые не имеют высшего образования). 4.5. Сложные суждения и условия их истинности Сложным называют суждение, имеющее два и более субъекта или (и) предиката. Например: «Вершинин и его жена работают продавцами и увлекаются бальными танцами». В этом суждении два субъекта «Вершинин», «жена Вершинина» и два предиката «работать продавцом» и «увлекаться бальными танцами». Наличие такого количества терминов позволяет включать в состав этого суждения четыре простых суждения: 1. Вершинин работает продавцом. 2. Вершинин увлекается бальными танцами. 3. Жена Вершинина работает продавцом. 4. Жена Вершинина увлекается бальными танцами. Таким образом, сложное суждение образуется из простых при помощи логических союзов. Так, в приведенном выше примере оно образовано при помощи союза «и». Смысл данного суждения можно было передать и при помощи другого союза, например, «как и ...» («Вершинин, как и его жена, работает продавцом»). Но если бы мы применили союз «или», то смысл суждения изменился бы очень существенно и получилось бы другое суждение: «Вершинин или его жена работают продавцами и увлекаются бальными танцами». В зависимости от характера союза, позволяющего менять смысл высказывания, суждения делятся на соединительные, разделительные и условные. Соединительным (конъюнктивным) называется суждение, образованное из простых суждений при помощи союзов «и», «а», «но», «также», «как и» и т. п. Например: «В магазине № 67 взорвана дверь, но кража не произведена», «Курсант Миркин, как и Бибарсов, живет в пос. Булгаково, а учится в Уфе». Для обозначения логического союза, при помощи которого образуется соединительное суждение, применяется логическая постоянная «» (иногда – «·» или «»), которая называется конъюнкцией. Каждое из простых суждений, из которых образовано соединительное суждение, называется конъюнктом и обозначается, как правило, какой-либо строчной латинской буквой (a, b, c, p, q, ...). Например, в символическом виде суждение «В магазине № 67 взорвана дверь, но кража не произведена» может быть записано так: «а & b», где «а» – простое суждение «В магазине № 67 взорвана дверь», «b» – простое суждение «В магазине № 67 кража не совершена», «&» – союз «но». Поскольку всякое сложное суждение состоит из простых, каждое из которых может быть как истинным, так и ложным, то для логики представляет интерес вопрос об истинности сложного суждения в целом. Например, как оценивать истинность соединительного суждения в целом, если один из составляющих его конъюнктов является ложным? На этот вопрос ответили еще древние стоики. Они говорили, что соединительное суждение ложно, если содержит хотя бы одно ложное высказывание. В современной логике для определения условий истинности сложных суждений применяются так называемые матрицы (таблицы) истинности (см. таблицу 4.4). Таблица 4.4
Из таблицы видно, что соединительное суждение «а & b» истинно лишь тогда, когда оба его составляющие «а» и «b» истинны. Если соединительное суждение состоит из большего количества конъюнктов, чем два, то данное условие его истинности все равно остается в силе. Если сложное суждение образовано при помощи логических союзов «или», «либо», то оно называется разделительным или дизъюнктивным. Например: «Вчера вечером Макеев был дома или находился у соседей». Данное суждение имеет один субъект «Макеев» и два предиката «Вчера вечером был дома» и «Вчера вечером находился у соседей». Оно состоит из двух простых суждений, которые называются дизъюнктами: 1 Вчера вечером Макеев находился дома. 2. Вчера вечером Макеев находился у соседей. Эти два простых суждения соединены в одно сложное при помощи союза «или», называемого дизъюнкцией и обозначаемого в виде знака «». В символическом виде приведенное выше разделительное суждение можно записать так: «а b», где «а» – первый дизъюнкт, «b» – второй, а «» – союз «или». Разделительное суждение бывает двух видов: строгая (сильная) дизъюнкция (исключающе-разделительное суждение) и нестрогая (слабая) дизъюнкция (соединительно-разделительное суждение). Они отличаются значением союза «или» («либо»). Дело в том, что союз «или» употребляется в двух смыслах – исключающем и неисключающем. В приведенном выше примере он употреблен в неисключающем смысле – ведь Макеев вчера вечером мог быть и дома, и у соседей. Один из этих дизъюнктов не исключает истинности другого. В этих случаях знак дизъюнкции употребляется без изменений («»). Более того, такое суждение истинно всегда, кроме одного случая: когда все составляющие его дизъюнкты ложны (см. таблицу 4.5). Таблица 4.5
Примером употребления союза «или» в исключающем смысле является следующее суждение «Вчера в восемь вечера Макеев был дома или находился у соседей». Очевидно, что Макеев не мог находиться в восемь вечера одновременно и дома, и у соседей. В этих случаях в логике применяется измененный знак дизъюнкции (например: «а Ú b», «а b»). Если союз «или» употребляется в исключающем смысле, то сложное суждение будет истинным лишь в тех случаях, когда один из его дизъюнктов является истинным, а остальные – ложными. Поэтому матрица истинности строгой дизъюнкции отличается от приведенной выше таблицы тем, что при строгой дизъюнкции все составляющие ее простые суждения не могут быть одновременно истинными. По этой причине первая строка этих таблиц не может быть одинаковой (см. таблицу 4.6). Таблица 4.6
Указанные условия истинности сохраняются и для тех случаев, когда разделительное суждение состоит более чем из двух дизъюнктов. Следующий вид сложных суждений – условное, или импликативное, суждение. Оно образуется из двух простых суждений, называемых основанием и следствием, соединенных между собой союзом «если ..., то ...». Роль основания всегда выполняет суждение, в котором указывается условие реализации следствия. Например: «Если вода замерзла, то температура воздуха ниже нуля». Здесь первая часть высказывания «если вода замерзла» является основанием, а вторая часть «то температура воздуха ниже нуля» – следствием. Рассмотрим другой пример: «Я не сдам экзамен, если не буду к нему готовиться». В приведенном примере основанием будет вторая часть высказывания (если не буду к нему готовиться), так как она выражает условие, а следствием – первая часть высказывания (я не сдам экзамен). Необходимо отметить, что в некоторых суждениях логический союз «если …, то …» может не выражаться в словесной форме, а лишь подразумеваться. Такое суждение также будет условным, если одно из простых суждений, входящих в его состав, будет выражать условие, а другое – вытекающее из него следствие. Например: «Любишь кататься, люби и саночки возить». Данное суждение можно записать как «Если любишь кататься, то люби и саночки возить». И, наоборот, в некоторых суждениях союз «если …, то …» может иметь место, но суждение не будет условным, если простые суждения, входящие в его состав, не будут выражать условие, и вытекающее из него следствие. Например: «Если раньше он работал на заводе, то теперь учится в вузе». В приведенном примере одно из суждений логически не следует из другого. Таким образом, в условных суждениях обязательно одна из его частей является основанием, а другая вытекающим из него следствием. В логике часто основание называют антецедентом, а следствие – консеквентом. Союз «если ..., то ...» называют импликацией и обозначают знаком «» или « ». Условное суждение в символическом виде записывается так: «a b» (или же «a b»), где «а» – основание, «b» – следствие, « » – союз «если ..., то ...». Условное суждение истинно всегда, за исключением одного случая: когда основание истинно, а следствие ложно. Поэтому матрица истинности условного суждения выглядит так (см. таблицу 4.7): Таблица 4.7
Анализ свойств условного суждения оказывается полезным для уяснения смысла таких важных для научного мышления понятий, как необходимость и достаточность условий для наступления определенного события. Условия называются достаточными для события, если их наличие непременно вызывает это явление. Например, в суждении «Если лицо совершило кражу, то оно подлежит уголовному наказанию» основание есть достаточное условие для следствия, так как факт совершения лицом кражи достаточен для привлечения лица к уголовной ответственности. Условия являются необходимыми для события, если данное событие не происходит без этих условий. Очевидно, что факт совершения кражи не является необходимым условием для привлечения человека к уголовной ответственности (ведь для этого достаточно, например, и совершения грабежа или разбоя). Поэтому в суждении «Если лицо совершило кражу, то оно подлежит уголовному наказанию» основание является достаточным, но не необходимым условием для следствия. В суждении же «Если эта общность является политической партией, то она имеет устав» условие будет необходимым, но недостаточным, так как кроме устава политическая партия, к примеру, должна иметь и программу. Если же основание является необходимым и достаточным условием для следствия, то мы имеем дело с суждением эквивалентности. В таком случае обычно применяют союз «если и только если ..., то ...» («тогда и только тогда»), который называется эквиваленцией и обозначается знаком «» (иногда «» или «»). Суждение, образованное при помощи этого союза, называют еще двойной импликацией. Пример: «Если и только если по факту кражи есть обвинительный приговор суда, то лицо, ее совершившее, может быть привлечено к уголовной ответственности». В символическом виде это суждение можно записать так: «а º b», что значит: из «а» следует «в», а из «в» следует «а». Например: из суждения «Если число четное, то оно делится на два» следует, что «Если число делится на два, то оно четное». Эквивалентное суждение истинно только тогда, когда входящие в него простые суждения либо одновременно истинны, либо одновременно ложны. Матрица истинности эквивалентного суждения выглядит так (см. таблицу 4.8): Таблица 4.8
На основании приведенных матриц истинности для отдельных суждений можно составить общую для них таблицу истинности (см. таблицу 4.9). Таблица 4.9
Структура и условия истинности сложного суждения может быть представлена также в виде таблицы 4.10. Таблица 4.10
Чтобы определить истинность сложного суждения, необходимо, во-первых, определить союз, с помощью которого простые суждения соединяются в составе сложного; и, во-вторых, установить истинность всего сложного суждения, используя таблицу истинности соответствующего суждения. Рассмотрим сказанное выше на примерах. Пример 1. Определить истинность сложного суждения «Приговор суда может быть обвинительным или же оправдательным», если известно, что первое простое суждение, входящее в состав сложного, истинно, а другое ложно. Решение: В приведенном примере простые суждения, входящие в состав сложного, соединены с помощью логического союза «или», следовательно, это разделительное суждение. В рассматриваемом суждении дизъюнкты исключают друг друга, значит – это строгая дизъюнкция (исключающее разделительное суждение). По условиям задачи первое простое суждение «Приговор суда может быть обвинительным» (а) – истинное, а второе «Приговор суда может быть оправдательным» (в) – ложное. Подставим полученные данные в таблицу истинности. Там стоит знак «и», что означает истинность сложного суждения. Пример 2. Определить истинность сложного суждения «Депутаты и ветераны войны пользуются жилищными льготами», если известно, что первое простое суждение, входящее в состав сложного, истинно, а второе ложно. Решение: Это соединительное суждение (конъюнкты соединены с помощью логического союза «и»). Оно может быть истинным только в том случае, если оба суждения, входящие в его состав, являются истинными. Но по условиям задачи, второе суждение является ложным, следовательно, все сложное суждение тоже является ложным. 4.6. Логическая характеристика вопроса и ответа Несмотря на то, что вопрос не является суждением и не может быть охарактеризован как истинное или ложное знание, тем не менее он занимает важное место в процессе познания. Особое место занимает логика вопроса и ответа при установлении истины судом, а также в процессе дознания, когда сомнения и неопределенность в мыслях неизбежно порождает вопросно-ответную форму общения. Поэтому логика уделяет достаточно большое внимание изучению вопросов. Существует даже специальная «Логика вопросов и ответов». Рассмотрим некоторые виды вопросов и ответов и основные требования, предъявляемые к их формулировке. Вопрос – это логическая форма, включающая исходную информацию с одновременным указанием на ее недостаточность с целью получения новой информации в виде ответа. В естественном языке вопрос выступает чаще всего в виде вопросительного предложения. Вопросы можно разделить на следующие две группы: 1. Вопросы к решению. Это вопросы, требующие выбора правильного ответа из множества заданных вариантов. Например: «Это преступление совершено путем действия или бездействия?», «Данное понятие единичное, общее или пустое?». 2. Вопросы к пополнению. В данном вопросе перечень возможных ответов не перечисляется, а предполагается, что лицо, которому задается вопрос, знает этот перечень или сможет узнать из каких-либо источников. Например: «Какое это понятие по объему?», «Какая наука изучает сущность права?». В зависимости от характера деятельности в процессе поиска ответа, вопросы принято делить на информационные, задачи и проблемы. Информационный вопрос решается путем поиска необходимой для ответа информации, которая имеется в каких-либо источниках. Например, вопрос: «Какие преступления характеризуются как квалифицированные?» является информационным. Ответ на этот вопрос можно найти в курсе уголовного права. Рассмотренные выше вопросы к решению и вопросы к пополнению также входят в класс информационных вопросов. В задаче ответ задан в ее условиях, но для нахождения этого ответа необходимо знать свойства и закономерности этих условий, то есть алгоритмы решения. Этот вид вопроса хорошо нам известен из курса школьной математики. Для ответа на вопрос-проблему нет достаточной известной человечеству информации, отсутствует алгоритм его решения. Например: «Можно ли создать аппараты, летающие со скоростью света?». Но не всегда вопрос, который считается автором проблемой, может быть действительно проблемой. Может оказаться, что этот вопрос уже решен в принципе для науки или практики, но автор для решения этого вопроса просто не достиг уже добытого обществом знания. Вопросы также делят на сильные и слабые. Сильный вопрос требует поиска всех истинных ответов. К разряду таких вопросов принадлежит вопрос, который имеет один истинный ответ. Слабый вопрос не содержит в себе максимальной полноты требования, достаточно перечислить лишь часть истинных ответов. Каждый вопрос содержит определенное знание, называемое логической предпосылкой вопроса. Например, логической предпосылкой вопроса: «Какие деяния уголовно наказуемы?» является знание, что существуют деяния, которые наказываются в уголовном порядке. Очень важно правильно поставить вопрос, что способствует наиболее быстрому нахождению истинного ответа. Логика выдвигает ряд основных требований к правильной постановке вопроса: 1. Вопрос должен формулироваться ясно, четко. Это правило предписывает задавать вопрос кратко, лаконично, без оговорок и отступлений. При употреблении в вопросе многозначных слов необходимо указывать то значение, которое имеется в виду. 2. Логические предпосылки вопроса должны быть истинными. Если хотя бы одна из предпосылок является ложной, то вопрос поставлен неправильно. Например, таковым является вопрос: «Где у женщины находится предстательная железа?», так как его предпосылка является ложной (у женщин эта железа отсутствует). Наличие логических предпосылок вопроса предполагает, что спрашивающий должен обладать какими-то знаниями в той области, которая его интересует. Например, юрист вряд ли задаст подобный вопрос: «Какие преступления не наказываются?», так как знает, что наказуемость – один из обязательных признаков содержания понятия «преступление». 3. При постановке вопроса необходимо учитывать возможность внушающего воздействия языка. Вопрос может быть задан с определенной эмоциональной нагрузкой, что может повлиять на ответ. Поэтому необходимо хорошо знать и ориентироваться на психологическое состояние отвечающего. Иной раз преподаватель, заметив неуверенность в ответах учащегося, пытается «завалить» его вопросами, что со стороны преподавателя является нарушением данного правила. Как известно, на один и тот же вопрос возможны разные ответы. Ответ, как правило, есть суждение, содержащее информацию, запрашиваемую в вопросе1. Как и вопросы, ответы можно классифицировать по разным основаниям. Различают следующие виды ответов: Истинные и ложные. Истинным является ответ, соответствующий действительности, ложным – несоответствующий. Полные и неполные. Полный ответ содержит информацию по всем составным частям вопроса, неполный (частичный) – только определенной его части (частям). Например, если на вопрос «Аркин и Бибарсов студенты?» следует ответ «Бибарсов – студент», то это неполный ответ. Этот ответ не содержит информацию об Аркине, поэтому не устраняет без остатка содержащуюся в вопросе неопределенность. Краткие и развернутые. Краткими являются односложные ответы «да» или «нет». Развернутым считается ответ, который содержит информацию по всем элементам вопроса. Например, кратким ответом на вопрос «Знаком ли Вам потерпевший?» будет «Да», а развернутым – «Да, потерпевший мне знаком». Прямые и косвенные. Прямым называется ответ, относящийся непосредственно к области поиска, указанной в вопросе, и не содержащий каких-либо сведений, выходящих за пределы вопроса. Косвенным называется ответ, содержащий информацию, непосредственно не запрашиваемую в самом вопросе. Прямым ответом на вопрос «Какой город является административным центром Калининградской области?» будет «Административным центром Калининградской области является город Калининград». Косвенным же ответом на этот вопрос является «Административным центром Калининградской области является бывший прусский город Кёнигсберг». Точные и неточные. В точном ответе содержится информация, достаточная для устранения отраженной в вопросе неопределенности. Неточный ответ не устраняет такую неопределенность. На вопрос «Кто создал теорию относительности?» точным ответом будет «Теорию относительности создал А. Эйнштейн», неточным – «Теория относительности возникла в ХХ веке». По существу и не по существу задаваемого вопроса. Ответ по существу вопроса (релевантный) содержит информацию, относящуюся к задаваемому вопросу. Ответ не по существу (нерелевантный) вообще не относится к задаваемому вопросу. На вопрос «Есть ли у потерпевшего автомобиль?» релевантным будет ответ «Да, у потерпевшего есть автомобиль», нерелевантным – «Потерпевший – больной человек». Знание логического механизма постановки вопросов и конструирования ответов на них служит рациональной основой успешного проведения допросов, освидетельствований, опознаний и других судебно-следственных действий. Выводы 1. Суждение – это форма мысли, выраженная в виде предложения, в котором что-либо утверждается или отрицается. Обычной формой выражения суждения выступает повествовательное предложение. Всякое суждение истинно либо ложно. Если мысль невозможно оценить с точки зрения истинности, она не является суждением. 2. Суждения делятся на простые и сложные. Простое суждение имеет субъект, предикат и связку. В сложном суждении количество субъектов или (и) предикатов больше двух. 3. Для деления простых суждений на виды в традиционной логике обычно применяется их объединенная классификация, которая выделяет четыре вида суждений: общеутвердительные (А), общеотрицательные (Е), частноутвердительные (I) и частноотрицательные (О). 4. Субъект и предикат суждения, будучи понятиями, могут находиться в различных отношениях. Анализ суждения с точки зрения отношения между объемами его субъекта и предиката называется определением распределенности терминов. Термин называется распределенным, если он своим объемом полностью входит в объем другого термина или полностью исключается из него. 5. Простые суждения могут находиться в различных отношениях друг к другу. Отношения между сравнимыми суждениями рассматриваются при помощи специальной схемы, называемой логическим квадратом. Она позволяет оценивать истинность суждения, находящегося в определенном отношении к другому суждению. 6. Сложные суждения делятся на соединительные, разделительные и условные. Истинность сложного суждения зависит от истинности его составляющих простых суждений и вида логического союза, при помощи которого оно образовано. Для определения истинности сложного суждения существуют матрицы истинности. 7. Вопрос – это логическая форма, включающая исходную информацию с одновременным указанием на ее недостаточность с целью получения новой информации в виде ответа. Ответ, как правило, есть суждение, содержащее информацию, запрашиваемую в вопросе. Вопросы для повторения 1. Что такое суждение? Чем оно отличается от предложения? 2. Из каких структурных элементов состоит суждение? 3. Как определить, является ли суждение простым или сложным? 4. Какие классификации простых суждений Вы знаете? 5. В каких отношениях между собой могут находиться простые суждения? 6. Какие виды сложных суждений Вы знаете? 7. Каково практическое значение знания об условиях истинности сложных суждений в вашей будущей профессиональной деятельности? 8. Какие виды вопросов Вы знаете? 9. Какие ответы не устраняют неопределенность, содержащуюся в вопросе? Тестовые задания к главе 4 1. Суждение – это … а) предложение; б) незаконченная мысль; в) обобщенное понятие; г) форма мышления; д) закон мышления. 2. Суждение выражается в форме … а) повествовательного предложения; б) вопросительного предложения; в) побудительного предложения; г) словосочетания. 3. Предмет суждения называется … а) сущностью; б) смыслом; в) субъектом; г) силлогизмом; д) связкой; е) предикатом. 4. … – элемент атрибутивного суждения, обозначающий какой-либо признак или свойство его субъекта, или то, что говорится о субъекте. а) предикат; б) субъект; в) квантор; г) связка. 5. … – указывает на объем субъекта простого суждения. а) предикат; б) субъект; в) квантор; г) связка. 6. Атрибутивными являются суждения: а) Сергей старше Ивана; б) существуют вечные законы мира; в) кинжал – огнестрельное оружие; г) душа существует; д) человек – это разумное живое существо; е) счастье есть, его не может не быть; ж) ты хочешь быть Наполеоном? з) некоторые люди имеют преступные наклонности; и) США более демократичная страна, чем Аргентина. 7. Какие суждения являются суждениями с отношением? а) Сергей старше Ивана; б) существуют вечные законы мира; в) кинжал – огнестрельное оружие; г) душа существует; д) человек – это разумное живое существо; е) счастье есть, его не может не быть; ж) ты хочешь быть Наполеоном? з) некоторые люди имеют преступные наклонности; и) США более демократичная страна, чем Аргентина. 8. Определите вид суждения по объединенной классификации: «Приговор – вид судебного решения». а) А; б) Е; в) I; г) О. 9. Определите вид суждения по объединенной классификации: «Этот пример не является ясным». а) А; б) Е; в) I; г) О. 10. Определите вид суждения по объединенной классификации: «Большинство рыцарей не лжецы». а) А; б) Е; в) I; г) О. 11. Определите распределенность терминов в следующем суждении: «Кража является видом хищения». а) оба термина распределены; б) субъект распределен, предикат – нет; в) оба термина не распределены; г) предикат распределен, субъект – нет. 12. Определите распределенность терминов в следующем суждении: «Ни одно государство не вправе вмешиваться в дела другого государства». а) оба термина распределены; б) субъект распределен, предикат – нет; в) оба термина не распределены; г) предикат распределен, субъект – нет. 13. Определите распределенность терминов в следующем суждении: «Близкий родственник подсудимого не может выступать на суде в качестве судьи». а) оба термина распределены; б) субъект распределен, предикат – нет; в) оба термина не распределены; г) предикат распределен, субъект – нет. 14. Определите распределенность терминов в следующем суждении: «Ю. Гагарин – первый космонавт на Земле». а) оба термина распределены; б) субъект распределен, предикат – нет; в) оба термина не распределены; г) предикат распределен, субъект – нет. 15. Определите распределенность терминов в следующем суждении: «Некоторые спортсмены являются мастерами спорта». а) оба термина распределены; б) субъект распределен, предикат – нет; в) оба термина не распределены; г) предикат распределен, субъект – нет. 16. Через «логический квадрат» установите истинность второго из приведенных суждений, если известно, что первое суждение ложно: «Некоторые обвиняемые не имеют права на защиту. Некоторые обвиняемые имеют право на защиту». а) истинно; б) ложно; в) неопределенно; г) данные суждения несравнимы. 17. Через «логический квадрат» установите истинность второго из приведенных суждений, если известно, что первое суждение ложно: «Ни одно нарушение норм морали не является правонарушением. В некоторых случаях нарушение норм морали не является правонарушением». а) истинно; б) ложно; в) неопределенно; г) данные суждения несравнимы. 18. Через «логический квадрат» установите истинность второго из приведенных суждений, если известно, что первое суждение ложно: «Некоторые жалобы были написаны на имя прокурора. Все жалобы были написаны на имя прокурора». а) истинно; б) ложно; в) неопределенно; г) данные суждения несравнимы. 19. Через «логический квадрат» установите истинность второго из приведенных суждений, если известно, что первое суждение истинно: «Истина – это знание, с которым все согласны. Истина – это знание, которое не всегда подтверждается». а) истинно; б) ложно; в) неопределенно; г) данные суждения несравнимы. 20. Через «логический квадрат» установите истинность второго из приведенных суждений, если известно, что первое суждение истинно: «Все кражи тайные хищения. Отдельные кражи не являются тайными хищениями». а) истинно; б) ложно; в) неопределенно; г) данные суждения несравнимы. 21. Какое суждение будет истинным при истинности суждения: «Все курсанты нашего взвода сдали зачет по физической подготовке»? а) некоторые курсанты нашего взвода не сдали зачет по физической подготовке; б) некоторые курсанты нашего взвода сдали зачет по физической подготовке; в) ни один курсант нашего взвода не сдал зачет по физической подготовке. 22. Какое суждение будет истинным при ложности суждения: «Каждый преступник должен быть привлечен к уголовной ответственности»? а) некоторые преступники должны быть привлечены к уголовной ответственности; б) ни один преступник не должен быть привлечен к уголовной ответственности; в) некоторые преступники не должны быть привлечены к уголовной ответственности. 23. Определите вид суждения и выразите его через принятую в логике символику: «Суждения находятся в отношении контрадикторности, если они не могут быть одновременно ложными». а) a & b; б) a \/ b; в) a Ú b; г) a É b; д) a º b. 24. Определите вид суждения и выразите его через принятую в логике символику: «В судебном заседании прокурор обязан либо поддерживать обвинение, либо отказаться от него». а) a & b; б) a \/ b; в) a Ú b; г) a É b; д) a º b. 25. Определите вид суждения и выразите его через принятую в логике символику: «Насилие при разбое может быть физическим или психическим». а) a & b; б) a \/ b; в) a Ú b; г) a É b; д) a º b. 26. Определите вид суждения и выразите его через принятую в логике символику: «Дождь не идет, но не жарко». а) a & b; б) a \/ b; в) a Ú b; г) a É b; д) a º b. 27. Определите вид суждения и выразите его через принятую в логике символику: «Некоторые подозреваемые являются душевнобольными или симулируют душевную болезнь». а) a & b; б) a \/ b; в) a Ú b; г) a É b; д) a º b. 28. Определите истинность сложного суждения, если известно, что второе суждение, входящее в его состав, ложно, а остальные истинны: «Если зима снежная, то год будет плодородным». а) истинно; б) ложно; в) неопределенно; г) невозможно определить. 29. Определите истинность сложного суждения, если известно, что второе суждение, входящее в его состав, ложно, а остальные истинны: «Это понятие либо общее, либо конкретное, либо безотносительное». а) истинно; б) ложно; в) неопределенно; г) невозможно определить. 30. Определите истинность сложного суждения, если известно, что первое суждение, входящее в его состав, ложно, а остальные истинны: «Если болезнь находится в зачаточном состоянии, то ее трудно распознать, но легко излечить». а) истинно; б) ложно; в) неопределенно; г) невозможно определить. 31. Определите истинность сложного суждения, если известно, что второе суждение, входящее в его состав, ложно, а остальные истинны: «Если число делится на 2, то оно четное». а) истинно; б) ложно; в) неопределенно; г) невозможно определить. |
