Логика. Учебное пособие (2018) (1). Учебное пособие Уфа 2018 удк 16 ббк 87. 4 И851 Рекомендовано к опубликованию
 Скачать 1.2 Mb. Скачать 1.2 Mb.
|
|
Условное умозаключение Условным называется умозаключение, в котором обе посылки являются условными суждениями. Например: Если число делится на восемь, то оно делится на четыре. Если число делится на четыре, то оно делится на два. Если число делится на восемь, то оно делится и на два. Иногда это умозаключение называют чисто условным силлогизмом (исходя из того, что все высказывания, входящие в его содержание, являются условными суждениями). Причем основание второй посылки является следствием первой посылки, из которой вытекает другое следствие. Вывод в этом умозаключении строится по правилу: следствие следствия есть следствие основания. Символически это записывается через следующую формулу: (а É в) (в É с) а É с Условно-категорическое умозаключение Условно-категорическим называют умозаключение, одна из посылок которого является условным, а другая посылка и заключение – категорическими суждениями. Например: Если приговор вынесен несправедливо, то он будет отменен. Данный приговор вынесен несправедливо. Следовательно, он будет отменен. Из примера видно, что первая посылка является сложным условным суждением, а вторая посылка и заключение – простым категорическим суждением. Для того чтобы мысль, построенная в виде условно-категорического умозаключения, была истинной, она должна соответствовать одной из двух правильных форм (правильным модусам): Утверждающий модус: а É в, а в Отрицающий модус: а É в, в а Если же мысль имеет другую форму, то ее заключение считается недостоверным и имеет вероятностный характер. Так, логически возможно построение еще двух модусов, которые являются неправильными формами вывода: Неправильный утверждающий модус: а É в, в а Неправильный отрицающий модус: а É в, а в Разберем на приведенном выше примере, как строится модус. Пример 1. Если пройдет дождь, то дороги будут мокрыми. Дождь прошел. Следовательно, дороги мокрые. Решение: Для определения правильности вывода необходимо записать умозаключение в символической форме и сравнить полученную формулу с утверждающим и отрицающим модусами условно-категорического умозаключения. Далее выделить условное суждение: это первая посылка – Если пройдет дождь, то дороги будут мокрыми. Из темы «Суждение» мы знаем, что условное суждение записывается следующим образом: а É в, где «а» – основание «Если пойдет дождь», «в» – следствие «дороги будут мокрыми». Во второй посылке, по сути, приводится основание «а» – дождь прошел, а в заключении – следствие «в» – дороги мокрые. Запишем посылки в числителе, а заключение – в знаменателе. Черту, разделяющую числитель и знаменатель, будем читать как слово «следовательно» (иногда – «значит»). Тогда вся символическая запись анализируемого умозаключения будет такой: а É в, а в При сравнении с модусами условно-категорического силлогизма оказывается, что это умозаключение имеет форму утверждающего модуса. Следовательно, умозаключение верное. Рассмотрим другой пример: Пример 2. Если пройдет дождь, то дороги будут мокрыми. Дороги мокрые. Следовательно, дождь прошел. Решение: Если пройдет дождь, то дороги будут мокрыми (а É в). Дороги мокрые (в). Следовательно, дождь прошел (а). Получаем следующую формулу: а É в, в а Она не соответствует ни одному правильному модусу данного силлогизма. Значит, умозаключение неправильное. Действительно, дороги могут быть мокрыми из-за того, что их полила специальная машина. Заключение этого силлогизма носит лишь вероятностный характер. Аналогичным образом строятся и отрицающие модусы. Рассмотрим, например, следующее умозаключение: Пример 3. Если я получу двойку, то не пойду в увольнение (а É в). В увольнение я пойду (в). Я не получил двойку (а). Решение: Данный силлогизм имеет следующую форму: а É в, в. а Это правильный отрицающий модус, значит, заключение здесь обоснованное. Таким образом, вывод в условно-категорическом умозаключении подчиняется двум правилам: 1. Из истинности основания (причины) логически вытекает истинность следствия, но из истинности следствия не вытекает истинность основания. 2. Из ложности следствия логически вытекает ложность основания, но из ложности основания не следует ложность следствия. Иногда вместо условного суждения в условно-категорических умозаключениях стоит суждение эквивалентности (а º в). В таких умозаключениях достоверные выводы получаются в любом из следующих модусов: а º в, а а º в, в а º в, в а º в, а в а а в Разделительно-категорическое умозаключение Разделительно-категорическим называется умозаключение, в котором одна посылка – разделительное, а другая – простое категорическое суждение. Например: Это преступление могло быть совершено путем действия или бездействия. Установлено, что оно совершено путем действия. Это преступление не совершено путем бездействия. Построим модус данного умозаключения. Разделительная посылка имеет следующую форму: а в, где а – «это преступление совершено путем действия», в – «это преступление совершено путем бездействия». Соответственно, вторую посылку обозначаем буквой а, а заключение является отрицанием в, т. е. в. Таким образом, получаем следующую формулу: а b, a b Если бы вторая посылка была «Установлено, что это преступление совершено путем бездействия», а заключение «Следовательно, оно не совершено путем действия», то умозаключение выглядело бы так: а b, b a В обоих случаях мысль движется одинаково: от утверждения одной альтернативы (во второй посылке) к отрицанию другой (в заключении). Поэтому такая форма мысли называется утверждающе-отрицающим модусом. Если мысль построена по этой форме, то должно соблюдаться следующее правило: посылка, являющаяся разделительным суждением, должна быть исключающе-разделительной (строгой дизъюнкцией). Посмотрим, что получается при нарушении этого правила на следующем примере: Это преступление совершил Симонов или Николаев (а в). Установлено, что преступление совершено Николаевым (в). Симонов не совершал этого преступления (а) Получаем следующую формулу: а в, в а Мысль здесь построена в виде утверждающе-отрицающего модуса. Следовательно, знание, полученное в результате этого умозаключения, будет достоверным лишь при условии исключения альтернативами друг друга в разделительной посылке. То есть заключение «Симонов не совершал этого преступления» будет истинным, если исключается совместное совершение данного преступления Симоновым и Николаевым. Если же есть хоть малейшее сомнение в этом, такое сомнение должно присутствовать и при оценке истинности заключения. Рассмотрим другой пример разделительно-категорического силлогизма: Это преступление совершено умышленно либо по неосторожности. Оно не совершено умышленно. Данное преступление совершено по неосторожности. В формализованном виде умозаключение будет выглядеть следующим образом: а b, a b – символ закрытой дизъюнкции. Если бы вторая посылка имела следующий вид: «Это преступление не было совершено по неосторожности», а заключение соответственно – «Оно совершено умышленно», то форма этого силлогизма была бы такой: а b,b a В обоих рассматриваемых случаях мысль движется от отрицания одной альтернативы (во второй посылке) к утверждению другой (в заключении). Такая форма мысли носит название отрицающе-утверждающего модуса и должна подчиняться следующему правилу: в посылке, являющейся разделительным суждением, должны быть перечислены все возможные для рассматриваемого случая варианты. В вышеприведенном примере вывод дает точное знание, так как преступления совершаются только умышленно или по неосторожности (других альтернатив нет). Теперь рассмотрим пример на нарушение данного правила: Правонарушитель несет гражданскую или уголовную ответственность. Правонарушитель С. не несет гражданской ответственности. Он несет уголовную ответственность. Получаем следующую формулу: а в, а в Так как это отрицающе-утверждающий модус, то согласно правилу в разделительной посылке должны быть перечислены все виды юридической ответственности. Но правило нарушено, поскольку не указаны административная и дисциплинарная виды ответственности. Следовательно, правило вывода по данному виду модуса нарушено, и заключение не является обоснованным. Проверим правильность следующих разделительно-категорических умозаключений. Пример 1. Понятия бывают общими, пустыми или конкретными. Это понятие конкретное. Следовательно, оно не общее и не нулевое. Решение: Для определения правильности умозаключения необходимо сначала узнать, в виде какого модуса оно построено. Для этого нужно записать его в символической форме. Здесь первая посылка состоит из трех альтернатив: «а», «в» и «с», разделенных союзом «или» («»). Значит, ее можно записать так: «а в с». Вторая посылка содержит утверждение третьей альтернативы «с». В заключении утверждается ложность первой «а» и второй «в» альтернативы. Следовательно, данное умозаключение имеет форму: а в с, с , а, в что соответствует утверждающе-отрицающему модусу. Для проверки его правильности нужно установить, исключают ли приведенные в разделительной посылке варианты друг друга. Вспомнив материал из раздела «Понятие и его виды», можно установить, что общее понятие «а» не может быть пустым «в», но оба они могут быть конкретными. Значит, «а» и «с», «в» и «с» не исключают друг друга, что является нарушением правила утверждающе-отрицающего модуса. Следовательно, умозаключение неправильное. Пример 2. Сейф открывал Нестеров. Это вытекает из того, что код замка знают только он и Сысоев. Но Сысоев в это время находился у начальника отдела. Другие люди в комнату, где находится сейф, не входили. Весь день в этой комнате работали только Сысоев и Нестеров. Значит, открывал сейф Нестеров. Решение: Умозаключение сначала нужно упростить. Оно может быть сформулировано короче: «Сейф могли открыть только Нестеров или Сысоев. Но Сысоев не мог это сделать. Значит, сейф открывал Нестеров». Теперь запишем его в символической форме: а в, в а Видно, что умозаключение имеет структуру отрицающе-утверждающего модуса. Значит, для установления его правильности нужно проверить полноту приводимых в разделительной посылке версий. В умозаключении на основании различных фактов утверждается, что версий только две: сейф при сложившихся обстоятельствах могли открыть только Нестеров и Сысоев. Тогда заключение «Сейф открывал Нестеров» обосновано. Условно-разделительный силлогизм Если умозаключение состоит одновременно из условного и разделительного суждений, то его называют условно-разделительным, или лемматическим. При этом количество условных суждений-посылок должно быть не менее двух. Такое умозаключение называют дилеммой. Если количество условных суждений-посылок равно трем, то умозаключение называют трилеммой. Если же количество условных суждений больше трех, то умозаключение называется полилеммой. На практике, как правило, чаще сталкиваются с дилеммами. Вот пример дилеммы, приведенной Сократом. Если результатом смерти является переход в небытие, то смерть есть благо (а É в). Если результатом смерти является переход в иной мир, то смерть есть благо (с É в). Смерть есть или переход в небытие, или переход в иной мир (а с). Следовательно, в любом случае смерть есть благо (в). Если записать данное умозаключение только при помощи символов, то получим следующую формулу: а É в, с É в, а с в Эта формула простой конструктивной (утверждающей) дилеммы. Но простая дилемма может быть и деструктивной (отрицающей). Например: Если убийство является заказным, то оно является квалифицированным преступлением (а É в). Если убийство является заказным, то жертва, как правило, не подвергается ограблению (а É с). Но данное убийство не является квалифицированным преступлением или жертва ограблена (в с). Следовательно, скорее всего, это убийство не является заказным (а): (а É в), (а É с), (в с) а Дилемма может быть и сложной. Например: Если убийство совершено психически здоровым человеком, то он должен понести уголовное наказание (а в). Если убийство совершено душевнобольным, то его следует поместить в специальное лечебное учреждение (с É d). Каждый убийца является психически здоровым или душевнобольным человеком (а с). Следовательно, убийцы должны подвергаться уголовному наказанию или помещаться в специальные лечебные учреждения (в d). Символическая запись такой сложной дилеммы будет выглядеть так: а É в, с É d, а с в d Полученная формула характеризует сложную конструктивную дилемму, в которой нет отрицания. Если же разделительная посылка и заключение дилеммы состоят из отрицательных суждений, то ее называют сложной деструктивной дилеммой. Вот пример такой дилеммы: Если Русин работает в банке, то он получает заработную плату. Если Русин является студентом, то он получает стипендию. Но Русин не получает заработную плату или не получает стипендию. Следовательно, он не работает в банке или не является студентом. Символическая запись этой дилеммы выглядит так: а É в, с É d, в d а с Все приведенные выше дилеммы являются правильными. Это становится ясным, если представить лемматические выводы в виде модусов условно-категорического силлогизма. Например, приведенный выше пример простой конструктивной дилеммы можно представить в виде двух условно-категорических выводов, имеющих одно и то же заключение: 1) Если результатом смерти является переход в небытие, то смерть есть благо. Смерть есть переход в небытие. Следовательно, смерть есть благо. Символическая запись этого силлогизма позволяет обнаружить, что он построен в виде утвердительного модуса условно-категорического силлогизма, следовательно, является правильным: а É в, а в В этой же дилемме содержится и другой условно-категорический силлогизм: «Если результатом смерти является переход в иной мир, то смерть есть благо. Результатом смерти является переход в иной мир. Следовательно, смерть есть благо». Видно, что он также построен в виде утвердительного модуса и по этой причине является правильным. В таком случае и вся дилемма правильна. Таким же образом анализируются и другие дилеммы: их следует рассматривать как совокупность двух условно-категорических умозаключений. Если же предметом анализа является трилемма или полилемма, то их следует представить в виде трех (трилемма) или более (полилемма) условно-категорических силлогизмов. В обобщенном виде приведенные выше рассуждения можно изобразить в следующих наглядных формах: Простая дилемма
Сложная дилемма
Рассмотрим примеры. Необходимо определить правильность выводов, сделанных в виде условно-разделительного умозаключения. Пример 1. Если хочешь быть счастливым, то нужно иметь много денег. Если хочешь быть счастливым, то нужно еще иметь и чистую совесть. Арсуев несчастен. Следовательно, у Арсуева нет большого количества денег или же совесть его не чиста. Решение: Сначала умозаключение нужно записать в символической форме. Тогда получим следующую форму: а É в, а É с, а в с Полученная форма соответствует неправильному модусу простой деструктивной дилеммы. Следовательно, вывод в этом умозаключении логически не обоснован. Пример 2. Если я пойду по лестнице, то сгорю. Если я выпрыгну из окна, то разобьюсь. Я не пойду по лестнице или не выпрыгну из окна. Тогда я не сгорю или не разобьюсь. Решение: При записи данного умозаключения при помощи логических переменных и постоянных получается следующая формула: а É в, c É d, а c в d Видно, что вывод построен в виде неправильной формы сложной деструктивной дилеммы, значит, он не может считаться обоснованным. Пример 3. Если войска потерпят поражение, то это грозит царю гибелью. Если войска победят, то это грозит царю зависимостью от них. Войска потерпят поражение или победят. Следовательно, царю грозит гибель или зависимость. Решение: Формализация умозаключения позволяет получить следующий модус: а É в, с É d, а с в d Он соответствует правильной форме сложной конструктивной дилеммы. Сокращенные, сложные и сложносокращенные силлогизмы Далеко не всегда силлогизмы применяются в полной форме. Очень часто встречается сокращенная форма дедуктивных умозаключений, которая в логике получила название энтимемы (от греч. «in thymos» – «в уме»). В ней одна из посылок или заключение не выражаются в языковой форме, а лишь подразумеваются. Следовательно, всякая энтимема состоит из двух и только двух суждений. Возьмем следующий силлогизм: Все преступники должны быть наказаны. Самарин – преступник. Самарин должен быть наказан. Из данного умозаключения можно образовать три энтимемы: «Все преступники должны быть наказаны, а Самарин преступник» (пропущено заключение), «Все преступники должны быть наказаны. Следовательно, Самарин должен быть наказан» (пропущена меньшая посылка), «Самарин – преступник, следовательно, он должен быть наказан» (пропущена большая посылка). Энтимемы также образуются из условно-категорических и разделительно-категорических силлогизмов. Проверку правильности энтимемы необходимо проводить по следующей методике: 1) восстановить энтимему до полной формы (сформулировать недостающую посылку или заключение); 2) определить вид умозаключения; 3) проверить обоснованность вывода по правилам данного умозаключения. Рассмотрим вышесказанное на примерах. Пример 1. Это убийство, поскольку оно совершено с особой жестокостью, является умышленным убийством при отягчающих обстоятельствах. Решение: Восстанавливаем умозаключение в полный вид. Видно, что в нем отсутствует большая посылка – «Если убийство совершено с особой жестокостью, то оно является умышленным убийством при отягчающих обстоятельствах». По логическим нормам большая посылка пишется вначале. Поставив ее на свое место, получаем силлогизм: «Если убийство совершено с особой жестокостью, то оно является умышленным убийством при отягчающих обстоятельствах. Это убийство совершено с особой жестокостью. Следовательно, оно является умышленным убийством при отягчающих обстоятельствах». Полученное умозаключение представляет собой условно-категорический силлогизм, следовательно, проверяем правильность вывода по правилам данного вида умозаключений (по рассмотренному в предыдущей главе алгоритму). Он проверяется путем сравнения с утверждающим и отрицающим модусами. Но для такого сравнения, как известно, умозаключение сначала нужно записать в символической форме: а É в, а в Такая форма мысли соответствует утверждающему модусу. Значит, вывод в этом умозаключении логически правильный. Пример 2. Обвиняемый имеет право на защиту, значит, Еремеев имеет право на защиту. Решение: Восстановив силлогизм в полный вид, получим следующее умозаключение: М Р Обвиняемый имеет право на защиту. S M Еремеев обвиняемый. S P Еремеев имеет право на защиту. Это простой категорический силлогизм. Проверим его правильность по правилам фигур. Для этого его посылки нужно записать при помощи терминов. Получается следующая схема: 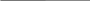  М Р М Р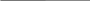 S М S МЭто первая фигура. Проверяем обоснованность вывода по ее правилам. В данном примере соблюдены все правила первой фигуры, значит, вывод обоснован. Соединение простых силлогизмов, в котором заключение предшествующего силлогизма становится посылкой последующего силлогизма, называется сложным силлогизмом или полисиллогизмом. Например: Все занимающиеся спортом – спортсмены. Все студенты нашей группы занимаются спортом. Все студенты нашей группы – спортсмены. Некоторые студенты нашей группы курят. Некоторые спортсмены курят. Если человек курит, он подрывает свое здоровье. Некоторые спортсмены подрывают свое здоровье. Различают два вида полисиллогизмов: прогрессивный и регрессивный. Если заключение предшествующего силлогизма становится большей посылкой для последующего силлогизма, то такой полисиллогизм называется прогрессивным. Если же заключение просиллогизма является меньшей посылкой в эписиллогизме, то полисиллогизм называется регрессивным. Тут следует сразу пояснить, что просиллогизмом в логике называют всякий предшествующий простой силлогизм по отношению к последующему в составе сложного силлогизма, а эписиллогизмом – всякий последующий простой силлогизм по отношению к предыдущему в составе полисиллогизма. В нашем примере полисиллогизм сначала имеет прогрессивную форму (до заключения «Некоторые спортсмены курят»), а затем – регрессивную. Анализ обоснованности вывода в полисиллогизмах осуществляется посредством приведения их к стандартной форме силлогизма и проверки обоснованности вывода в каждом из простых силлогизмов, входящих в состав сложного по соответствующим правилам. Часто полисиллогизмы принимают сокращенную форму: некоторые из их посылок опускаются. Полисиллогизм, образованный из связанных друг с другом простых силлогизмов путем исключения из них посылок, являющихся заключениями просиллогизмов, называется соритом. Например: Общественно опасные деяния аморальны. Преступление – общественно опасное деяние. Кража – преступление. Кража – аморальное деяние. Здесь пропущено заключение первого простого силлогизма «Преступление – аморальное деяние», которое является посылкой второго простого силлогизма. Второй силлогизм в полном виде выглядел бы следующим образом: Преступление – аморальное явление. Кража – преступление. Кража – аморальное явление. Соответственно двум видам полисиллогизмов существуют два вида соритов: гоклениевский (по имени немецкого логика Р. Гокления, впервые описавшего этот сорит), который возникает из прогрессивного полисиллогизма, и аристотелевский (впервые был описан Аристотелем), возникающий из регрессивного полисиллогизма. Приведенный выше пример является примером гоклениевского полисиллогизма. Следующий сорит является аристотелевским: Все преступления уголовно наказуемы. Кража – преступление. Все уголовно наказуемые деяния общественно опасны. Кража общественно опасна. В этом сорите пропущено заключение просиллогизма «Кража уголовно наказуема», которое является меньшей посылкой для эписиллогизма. Анализ обоснованности вывода сорита осуществляется посредством восстановления по смыслу подразумевающихся промежуточных заключений, получением полного полисиллогизма. Дальнейший его анализ проводится по правилам полисиллогизма. К сложносокращенным силлогизмам также относят и эпихейрему, в которой обе посылки являются энтимемами. Например: Ложь вызывает недоверие, так как она не соответствует истине. Лесть есть ложь, так как она есть умышленное извращение истине. Лесть вызывает недоверие. Каждая посылка в данном умозаключении является сокращением простого категорического силлогизма, т. е. энтимемой. Первая посылка, если ее развернуть до полной формы, будет выглядеть так: Всякое утверждение, не соответствующее истине, вызывает недоверие. Ложь есть утверждение, не соответствующее истине. Ложь вызывает недоверие. Вторая посылка при восстановлении будет состоять из следующего рассуждения: Всякое умышленное извращение истины есть ложь. Лесть есть умышленное извращение истины. Лесть есть ложь. Для проверки обоснованности вывода в эпихейреме ее нужно развернуть в полный полисиллогизм и проанализировать по правилам полисиллогизма. 5.3. Индуктивные умозаключения. Методы научной индукции Общая характеристика индуктивных умозаключений Индукцию обыкновенно понимают как метод исследования, при котором мысль движется от единичного или частного знания к общему. С другой стороны, индукция выступает как вид умозаключения. Индуктивным называют умозаключение, протекающее в форме обобщения, когда на основе повторяющегося признака у отдельных предметов (явлений) делается заключение о его принадлежности всем предметам (явлениям) данного класса. Например, если известно, что A, B, C, D, E обладающие свойством х, принадлежат к классу М, к этому же классу принадлежит F, то можно сделать вывод, что, вероятно, и F обладает свойством х:   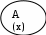     Индуктивное умозаключение сформировалось в процессе многовековой общественно-исторической практики людей из потребности в обобщении, то есть получении знаний о более или менее общих свойствах предметов и явлений окружающего мира. Когда при выделке топора быстро шлифуется один камень о другой, то трущиеся камни нагреваются; когда при сооружении лодки выскабливается древесина из ствола дерева, то нагреваются и дерево, и нож; когда волочат большое сухое дерево по земле, то трущаяся часть дерева нагревается и т. д. Наблюдая отдельные предметы и явления, люди приходили к общему правилу. В данном случае делалось заключение, что температура тела повышается от трения. От единичных суждений человек шел к общим суждениям, в которых выражалось знание общих закономерностей. Теоретическое мышление вообще не было бы возможно, если бы человек не устанавливал общее в разных явлениях посредством индукции. Так, Д. И. Менделеев открыл периодический закон химических элементов благодаря глубокому и тщательному изучению отдельных элементов. Все вышеизложенное не означает, что нельзя вывести одни общие правила из других. Точно также общие знания можно получить из книг и других источников информации. Так, о выделении тепла при трении современный школьник вполне может узнать из школьного курса физики, а не из собственных опытов. Но так или иначе первоначальные общие знания, правила, законы были получены путем индукции, в процессе опытного и практического освоения окружающей действительности. В этом и состоит огромная заслуга индуктивных умозаключений как метода познания. Правда, если в дедуктивных умозаключениях при наличии истинных посылок и правильном строении вывод всегда достоверный, то в индуктивных умозаключениях он может быть как достоверным, так и вероятным (правдоподобным). При этом степень вероятности здесь может быть самой различной – от маловероятных, самых приближенных и грубых обобщений, до более или менее точных, определенных, почти достоверных. Как и любое умозаключение, индукция состоит из посылок, в которых содержится полученная опытным путем информация, и заключения, представляющие собой общее суждение, фиксирующее некую закономерность или правило. Разница в том, что в дедукции посылками служат общие (или частные) суждения, а здесь характерны единичные суждения, поскольку в них выражено знание об отдельных предметах (хотя может быть знание и об их отдельных группах). Существенное отличие заключения в индуктивных умозаключениях от дедуктивных состоит в том, что по своему характеру оно общее (хотя может быть и частным, о части предметов какого-либо класса), тогда как в дедукции оно может быть и частным, и единичным. Логическим основанием вывода в индуктивном умозаключении служит логическая связь между посылками и заключением, в которой отражается объективная связь между отдельным и общим, причиной и следствием и т. д., которая делает возможным перенос знания с отдельных предметов на классы или с одних, менее общих классов на другие, более общие. Виды индукции Различают полную и неполную индукцию. Поскольку всякая индукция представляет собой обобщение, то их различие обусловлено главным: изучены ли для этого обобщения элементы того или иного класса полностью или же частично. Полная индукция имеет место тогда, когда посылки исчерпывают весь класс предметов, подлежащих обобщению. Например: Иванов болел гриппом. Петров болел гриппом. Сидоров болел гриппом. Все они живут в комнате № 10 . Все, живущие в комнате № 10, болели гриппом. Полную индукцию можно применить, когда мы имеем дело с закрытым классом предметов, число элементов в котором является конечным и легко обозримым. Заключение, получаемое в результате полной индукции, является категорическим суждением. В приведенном выше примере вывод является достоверным при условии, что речь идет о трехместной комнате, в которой кроме перечисленных людей больше никто не живет. В индуктивных умозаключениях предикат посылок и заключения всегда один и тот же, иначе нельзя сделать общий вывод. Это видно на нашем примере. В правовой сфере полная индукция может иметь место тогда, когда возникает необходимость анализа всех однотипных доказательств, имеющих отношение к расследуемому делу: проверка всех без исключения лиц, документов, вещественных доказательств, машин и т. д. Но, отдавая должное полной индукции, надо отметить, что в реальном человеческом познании она занимает меньше места, чем неполная индукция, так как с полным набором всех случаев человек имеет дело реже, чем с их неполным набором. Неполная индукция – это умозаключение, в котором общий вывод обо всем классе предметов делается на основании знания лишь некоторых предметов данного класса. Например: Железо – твердое тело. Медь – твердое тело. Золото – твердое тело. Серебро – твердое тело. Железо, медь, золото, серебро – металлы. Все металлы – твердые тела. Заключение при неполной индукции носит вероятностный характер, поскольку рассматривается не каждый предмет данного класса, а лишь часть предметов. В нашем примере мы рассмотрели далеко не все известные металлы, поэтому и получили ложный вывод, так как существуют и нетвердые металлы, например, ртуть. В связи с этим, несмотря на то, что в отличие от полной индукции с помощью неполной индукции можно делать обобщения относительно большого класса предметов, она также имеет существенный недостаток, заключающийся в опасности получения недостоверного вывода. Полная же индукция исключает такую опасность. Так, во многих учебниках логики приводится пример с выводом, полученным на основании неполной индукции – «Все лебеди белые», который оказался несостоятельным, когда в Австралии впервые обнаружили черных лебедей. Неполная индукция делится на два вида: популярную и научную. Популярная индукция – это вывод о всем классе предметов на основании знания некоторых предметов данного класса при условии, что не встречалось противоречащих нашему заключению случаев. Так, при исследовании причин преступности среди несовершеннолетних, анализируя их бюджет свободного времени, мы берем сто первых попавшихся несовершеннолетних и делаем общее заключение по этому вопросу для всех несовершеннолетних города или республики. Это и будет популярной индукцией. Такая индукция, принося определенную пользу, может применяться лишь на начальном этапе исследования, когда происходит процесс накопления фактического материала. Повседневная жизнь людей дает массу примеров популярной индукции. Так, люди не раз наблюдали, что ласточки перед дождем летают низко над землей. На этой основе был сделан вывод: «Ласточки всегда перед дождем летают низко над землей». Подобных примет, сделанных на основе непосредственных наблюдений, зафиксировано народной мудростью немало. Вот почему они получили название «народные приметы», а сама индукция – наименование «популярная» (народная). Однако такие выводы носят характер лишь вероятного знания. Достаточно встретиться противоречащему случаю, чтобы заключение оказалось ложным. Вероятность заключения научной индукции выше, чем популярной. Научная индукция – это общий вывод о всем классе предметов на основании знания необходимых признаков и причинных связей лишь некоторых предметов данного класса. Если в приведенном выше примере отбор несовершеннолетних осуществлялся бы в соответствии с определенным процентом школьников, учащихся училищ и колледжей, при этом из разных районов исследуемого региона (говоря языком социологии, соблюдалась бы репрезентативность выборки), то это была бы научная индукция. Виды индукции   Полная Неполная   Научная Популярная Несмотря на то, что вывод по неполной индукции является вероятностным, существует ряд условий, которые повышают степень достоверности такого вывода: 1. Необходимо рассматривать возможно большее количество случаев для индуктивного обобщения. Если мы будем исследовать вопрос о существовании внеземной жизни, то вывод будет более вероятен в том случае, когда мы исследуем двести планет, нежели только две. 2. Факты, подлежащие индуктивному обобщению, должны быть более разнообразны и по возможности более полно характеризовать предмет индуктивного обобщения. Вывод о существовании внеземной жизни будет более вероятным, если мы будем сравнивать планеты между собой по разнообразным основаниям (околопланетное пространство, грунт, водоемы, удаленность от звезды и т. д.). 3. Вероятность вывода по неполной индукции повышается, когда предметы, подлежащие индуктивному обобщению, обладают внутренней связью. То есть наш вывод будет вероятнее при исследовании планет Солнечной системы или других звездных систем, входящих в нашу Галактику. Если же мы будем исследовать планеты разных галактик, то вывод будет менее достоверным. 4. В качестве основы для индуктивного обобщения необходимо брать более существенный признак или группу признаков. В нашем примере это должны быть условия, необходимые и достаточные для существования жизни (наличие кислорода, воды, определенной оптимальной температуры, при которой возможна жизнь, и т. д.). Среди ошибок, возникающих при индукции, выделяют три, наиболее часто встречающиеся: 1. «Поспешное обобщение». Эта ошибка возникает тогда, когда в посылках индуктивного умозаключения не учтены все обстоятельства, которые, может быть, и являются причиной исследуемого явления. Эту ошибку совершил итальянский тюремный врач Ч. Ломброзо, когда на основании сходства отдельных антропологических признаков у некоторых преступников сделал ошибочное заключение, что причиной преступности являются биологические качества человека. Другой пример: «Курсант Сидоров позавчера не подготовился к занятиям, вчера не подготовился к занятиям и сегодня то же не готов», и на этом основании сделали вывод: «Курсант Сидоров вообще не готовится к занятиям». Но вывод может оказаться поспешным, так как по каким-то причинам он последние три дня не имел возможности подготовиться к занятиям. «Поспешное обобщение» особенно опасно при решениях трудовых, имущественных споров, расследовании уголовных дел. Ведь за допущенной ошибкой может стоять судьба человека. 2. «После этого, значит, по причине этого». Источник такой ошибки – смешение причинной связи с простой последовательностью во времени. Далеко не всегда предшествующее явление выступает причиной последующего, хотя, на первый взгляд, кажется именно так. Например: так, за зимой следует весна, но это еще не значит, что зима – причина наступления весны. Подобная ошибка нередко допускается в следственной практике. Предположим, что заболевший гражданин Зубов пришел к врачу, который ему сделал укол. На следующий день Зубов скончался. Можно ли отсюда сделать вывод, что причиной его смерти явился укол, сделанный врачом? Тут могло быть простое совпадение во времени. Причина же смерти могла быть совсем иной. На этой ошибке основаны многие суеверия. Если суеверный человек видит черную кошку, перебегающую ему дорогу, он считает ее причиной будущего несчастья, совершая при этом, с точки зрения логики, вышеназванную ошибку. 3. «Подмена условного безусловным». Данная ошибка может возникнуть в тех случаях, когда не учитывается следующее: всякая истина проявляется в определенном сочетании условий, изменение которых может повлиять и на истинность заключения. Например, если в обычных условиях вода замерзает при температуре 0º С, то с изменением этих условий (например, вода течет), температура замерзания понижается. Методы научной индукции Это довольно простые и часто применяемые в повседневной практике логические методы установления причинных связей. Впервые в четкой форме они были сформулированы английским философом Ф. Бэконом (1561–1626), а затем были усовершенствованы другим английским ученым – Дж. С. Миллем (1806–1873). Методы научной индукции      Метод сходства Метод различия Метод остатков Метод сопутствующих изменений Объединенный метод сходства и различия 1. Метод сходства. Если множеству случаев появления одного и того же события предшествует одно и то же явление, то оно, вероятно, и есть причина интересующего нас события. В формализованном виде эту мысль можно изобразить так: А, В, С, D x B, R, N, A x K, L, N, B x C, D, B, R x B x Из данной схемы видно, что из множества предшествующих обстоятельств во всех четырех исследуемых нами случаях присутствует лишь одно общее обстоятельство – В. Отсюда делаем заключение, что вероятной причиной явления х является обстоятельство В. С помощью этого метода можно определить причину явления радуги. Наблюдая ряд случаев ее появления: во время дождя, на утренней росе, в водяной пыли у водопада, при прохождении солнечного света через стеклянную призму, мы замечаем, что, несмотря на все различия между ними, они сходны в одном – прохождении солнечного луча через прозрачное тело определенной формы. Это и дает логическое основание сделать вывод о причине радуги во всех случаях ее появления. Точное заключение по этому методу можно сделать при соблюдении двух условий: а) если известны все предшествующие обстоятельства, которые представляют закрытое множество известных причин; б) если известно, что каждое из обстоятельств не вступает во взаимодействие с другими. 2. Метод различия. Если при наличии определенного явления событие наступает, а при его отсутствии – нет, то это явление и есть возможная причина исследуемого явления. Этот метод в формализованном виде можно записать так: A, B, C, D x B, C, D x A x Наличие обстоятельства А в системе всех предшествующих обстоятельств порождает явление х, а его отсутствие влечет за собой отсутствие явления х. Значит, вероятной причиной х является обстоятельство А. При этом нужно отметить, что метод различия дает более вероятное знание, чем метод сходства. Приведем следующий пример по применению данного метода. Растение, помещенное в темную комнату, в которую не проникали лучи солнечного света, практически не имело зеленой окраски либо окраска была очень бледной. Растение же, находящееся постоянно под солнечными лучами, имело ярко-зеленую окраску. Было сделано заключение, что солнечные лучи необходимы для выработки растением хлорофилла – вещества, придающего ему зеленую окраску. 3. Метод сопутствующих изменений. Явление, изменяющееся всякий раз, когда изменяется другое явление, составляет следствие или причину этого явления или связано с ним какой-нибудь общей причиной. Если обозначить буквами А, В, С предшествующие обстоятельства, х – интересующее нас явление, а цифрами 1, 2, 3 – степень изменчивости, то в формализованном виде этот метод выглядит следующим образом: А, В, С1 х1 А, В, С2 х2 А, В, С3 х3 С х Видно, что явление х изменяется с такой же степенью, как и обстоятельство С, при этом другие обстоятельства остаются неизменными. Следовательно, вероятной причиной х является С. Этим методом пользовался А. Л. Чижевский, устанавливая зависимость социальных процессов от явлений, происходящих на Солнце. Он заметил, что с появлением солнечных пятен активизировались боевые действия на фронтах Первой мировой войны. На основе своих наблюдений Чижевский делает вывод о причинно-следственной связи солнечной активности с процессами, происходящими в обществе. Метод сопутствующих изменений применяют обычно на начальном этапе исследования. Обоснованность заключения в выводе по этому методу определяется числом рассмотренных случаев, точностью знания о предшествующих обстоятельствах, а также адекватностью изменений предшествующего обстоятельства и исследуемого явления. Нужно также иметь в виду, что для исследователя интерес должны представлять не любые, а лишь пропорционально нарастающие или убывающие изменения. Те из них, которые не отличаются взаимно-однозначной регулярностью, нередко возникают под воздействием неконтролируемых, случайных факторов и могут вводить в заблуждение исследователя. 4. Метод остатков. Если вычесть из данного явления ту его часть, о которой известно, что она есть следствие определенных предшествующих обстоятельств, то тогда оставшаяся часть (остаток) явления будет следствием остальных предшествующих обстоятельств. На языке символов этот метод можно записать так: |
