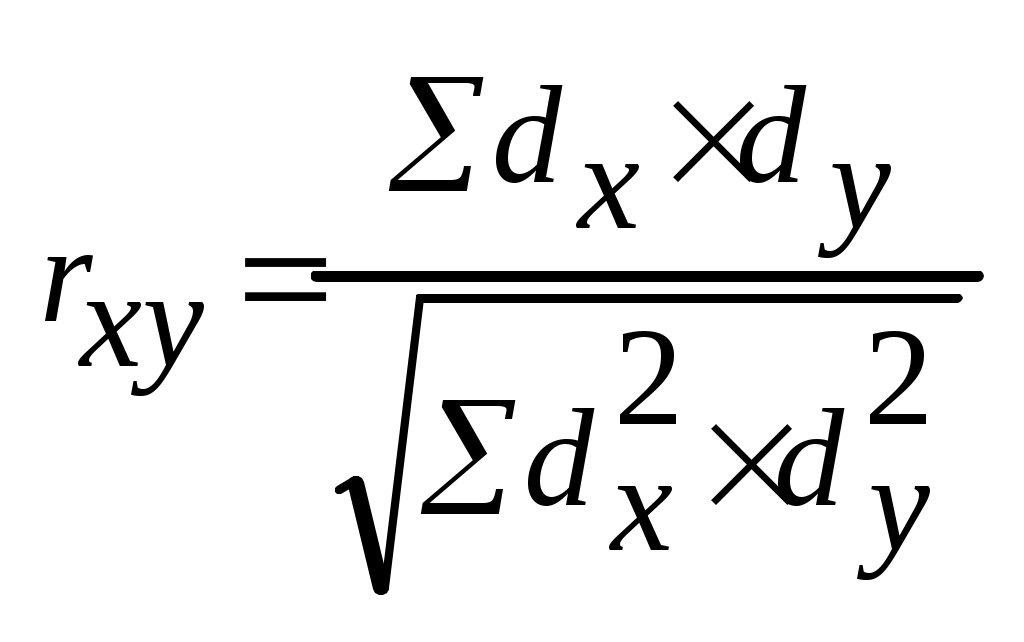Учебное пособие управляющего типа Агарков В. И., Бутева Л. В. Грищенко С. В. Донецк Донгму, 2006. 277 с

• Название: Учебное пособие управляющего типа Агарков В. И., Бутева Л. В. Грищенко С. В. Донецк Донгму, 2006. 277 с
• Дата: 24.03.2023
• Размер: 3.03 Mb.
• Имя файла: Posobie_po_med_statistike.doc
• Тип: Учебное пособие; #1011845
• страница: 26 из 35

ЦЕЛИ ЗАНЯТИЯ

Общая цель: уметь статистически устанавливать наличие и степень связи между явлениями при анализе здоровья населения.

Общая цель достигается через конкретные уменья:

1. 
   Решить вопрос о возможности наличия связи между явлениями.
   
2. 
   Определить вид связи.
   
3. 
   Выбрать наиболее целесообразную методику измерения корреляционной связи в каждом конкретном случае.
   
4. 
   Рассчитать показатель корреляционной связи.
   
5. 
   Оценить достоверность полученных результатов.
   
6. 
   Определить силу и направление связи.
   
7. 
   Сделать выводы о степени связи, ее силе и направлении.
   

ИСТОЧНИКИ УЧЕБНОЙ ИНФОРМАЦИИ

(рекомендуемая литература)

1. 
   Соціальна медицина та організація охорони здоров’я / Під ред. Вороненка Ю.В., Москаленка В.Ф. – Тернопіль: Укрмедкнига, 2000. – С. 82-87.
   
2. 
   Социальная гигиена и организация здравоохранения / Под ред. Серенко А.Ф., Ермакова В.В. – М.: Медицина, 1984. – С. 149-160.
   
3. 
   Руководство к практическим занятиям по социальной гигиене и организации здравоохранения / Под ред. Лисицына Ю.П., Копыта Н.Я. – М.: Медицина, 1984. – С. 65-68.
   
4. 
   Руководство по социальной гигиене и организации здравоохранения / Под ред. Лисицына Ю.П. – М.: Медицина, 1987. – Т.1. – С. 262-267.
   
5. 
   Граф логической структуры содержания темы (приложение 1).
   

ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ ТЕМЫ

1. 
   Виды связи между явлениями (признаками).
   
2. 
   Сущность корреляционной связи, ее разновидности.
   
3. 
   Методы вычисления коэффициента корреляции.
   
4. 
   Оценка достоверности коэффициента корреляции.
   
5. 
   Определение характера, силы, направления связи.
   
6. 
   Методика вычисления коэффициента линейной корреляции.
   
7. 
   Методика вычисления коэффициента ранговой корреляции.
   
8. 
   Методика вычисления коэффициента ассоциации.
   

ОСНОВНЫЕ ВОПРОСЫ И КЛЮЧЕВЫЕ ПОНЯТИЯ,

НА КОТОРЫЕ СЛЕДУЕТ ОБРАТИТЬ ВНИМАНИЕ

ПРИ ПОДГОТОВКЕ ТЕМЫ

Различные явления или признаки могут иметь между собой две формы связи: функциональную и корреляционную.

Функциональная связь характерна для явлений, между которыми существует строгая зависимость, то есть изменение на определенную величину одного явления (признака) сопровождается строго определенным изменение другого явления (признака). При этом зависимость проявляется настолько сильно, что каждому определенному значению влияющего признака (х) всегда соответствует строго определенное, единственное значение результативного признака (у). Такая связь встречается только в идеальных условиях, когда предполагается, что никаких посторонних влияний нет.

Функциональная связь в основном имеет место в естествознании и технике, где ее можно представить в виде уравнения, формулы (например, радиусу круга соответствует определенная площадь круга, объем шара зависит от длины его радиуса, скорость свободно падающего тела определяется величиной ускорения силы тяжести и временем падения, степень расширения тела определяется температурой нагревания и т.п.).

В медицинской практике мы, как правило, сталкиваемся с корреляционной связью. Корреляционная связь – это связь, при которой от изменения одного явления зависит главным образом, но не исключительно, изменение другого явления, значения которого варьируют в определенных размерах вокруг своей средней величины. Например, известно, что масса тела человека зависит от изменения его роста. Однако у группы лиц с одинаковым ростом можно наблюдать различные колебания массы тела. Эти колебания массы тела варьируют в определенных размерах вокруг своей средней величины, т.к. связаны еще с питанием, физической нагрузкой, обменом веществ, состоянием здоровья и т.п. Это связь между явлениями, проявляющаяся не в каждом конкретном случае, а при массовом наблюдении рассматриваемых признаков, т.е. совокупностей.

Корреляционная связь характерна для социально-гигиенических процессов, клинической медицины и биологии. Например, связь уменьшения уровня инфекционной заболеваемости с увеличением процента привитых лиц, взаимосвязь между цветом волос и цветом глаз (темные или светлые), зависимость заболеваемости раком кожи от степени пигментации кожных покровов, связь между уровнем вредных производных факторов и частотой профессиональных заболеваний.

По своему характеру корреляционная связь подразделяется на следующие виды:

• 
  причинно-следственную;
  
• 
  обусловленную;
  
• 
  параллельную.
  

Причинно-следственная связь проявляется в тех случаях, когда изменение одного явления (признака) является причиной изменения другого явления (признака). Например, увеличение числа диспансерных больных, получивших противорецидивное лечение, приводит к снижению частоты обострения хронических заболеваний, внедрение новых технологий на производстве приводит к изменению показателей производственного травматизма.

Обусловленная связь присутствует в тех случаях, когда изменение одного явления (признака) как бы создаст условия, способствующие изменению другого явления или признака. Например, высокая температура воздуха в летнее время может привести к росту частоты сердечно-сосудистых заболеваний, увеличению уровня пищевых отравлений среди населения, а понижение температуры воздуха в зимнее время сопровождается увеличением уровня заболеваемости населения простудными болезнями. Но при наличии ряда обстоятельств (например, проведение профилактических мероприятий) этого может не произойти.

Для параллельной связи характерно параллельное изменение двух явлений или признаков в зависимости от третьего. Например, изменение роста ребенка сопровождается изменением массы его тела и окружности груди. Но параметры таких изменений неодинаковы.

Различают прямолинейную и криволинейную корреляционную связь. Так, если при относительно равномерном изменении средних значений одного признака проходят равные изменения другого (например, соответствия между изменениями уровней максимального и минимального артериального давления) наблюдается прямолинейная корреляционная связь. При криволинейной зависимости равномерное изменение одного признака сопровождается неравномерными, непропорциональными возрастающими и убывающими изменениями другого признака.

Используя методы корреляции, важно помнить о возможности измерить связь между различными признаками только лишь в качественно однородной совокупности. Нельзя, например, сопоставлять рост и массу тела лиц разного пола и возраста.

Способами изображения (представления) связи могут быть:

• 
  таблицы,
  
• 
  рисунки (графики)
  
• 
  коэффициенты корреляции.
  

В таблицах коррелируемые данные представляют в виде корреляционных рядов или корреляционной решетки.

Корреляционный ряд – это ряд числовых изменений определенного явления (признака). В корреляционной таблице минимально может быть два таких ряда. Один из них (х) относится к влияющему признаку, а другой (у) – к результативному (табл. 1).

Таблица 1

Схема корреляционной таблицы

Vх	Vу
Х1	У1
Х2	У2
. . .	. . .
Хn	Уn

Корреляционная решетка – таблица, в которой каждому значению влияющего признака (х) относится несколько значений результативного признака (у). При этом каждому сочетанию х и у соответствует определенное поле (см. табл. 2).

Таблица 2

Схема корреляционной решетки

Vх	Vу
	У1	У2	…	Уn
Х1
Х2
. . .
Хn

Примечание: Х₁, Х₂, Х₃ и т.д. – разновидности одного явления (признака);

У₁, У₂, У₃ и т. д. – разновидности другого явления (признака).

Следует обратить внимание на то, что изучаемые явления (признаки) могут быть выражены количественно или описательно, представлены сгруппированными или несгруппированными данными.

Выразить количественно – это значит выразить числом (например, рост – в сантиметрах или метрах, массу тела – в килограммах, содержание железа в крови – в мг%, частоту заболеваний в промиллях или продецимиллях), а выразить описательно – значит выразить словесно. Описательные признаки – обычно альтернативные признаки. Альтернативным называют случай, когда вариация исчерпывается двумя возможностями: заболел или не заболел, привит или не привит, выздоровел или не выздоровел.

Сгруппированные данные – это данные, объединенные в группы по их величине в пределах одного интервала. В виде сгруппированных данных могут быть представлены значения одного из изучаемых явлений (признаков) или значения обоих признаков: влияющего (х) и результативного (у). Чаще всего группируют данные при большом числе наблюдений.

Более подробно о сгруппированных рядах см. в теме «Средние величины».

Несгруппированные данные – это данные каждого из изучаемых признаков, выраженные одним числом (см. табл. 6 и 11).

Еще одним способом демонстрации корреляционной связи являются графики (рисунки), которые дают представление о ее наличии и направлении (см. рис. 1).

Распределение точек на рисунке показывает, что они широко рассеяны вокруг линии. Их общее направление соответствует прямой линии. Тенденции к образованию кривой незаметно. Средние величины весьма близко подходят к прямой линии. В этом случае мерилом связи должен быть выбран коэффициент корреляции.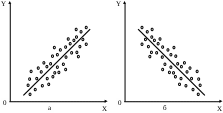



Рис. 1. Линейная корреляция между величинами Х и У

а – положительная, прямая;

б – отрицательная, обратная.

Если размещение точек на графике грубо похоже, по очертанию на перевернутую букву U и прямой линией описать его было бы невозможно (см. рис. 2), тогда коэффициент корреляции применять не следует. Для этого существуют другие методы анализа.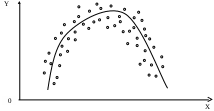



Рис. 2. Криволинейная зависимость между величинами Х и У

Таким образом, таблицы и графики дают лишь представление о наличии и направлении связи. Однако измерить и оценить статистическую достоверность этой связи можно при помощи коэффициента корреляции.

Существует много способов вычисления таких коэффициентов. Выбор одного какого-либо из них находится в зависимости от следующих факторов:

1. 
   Каким образом выражены признаки изучаемых явлений; находящихся во взаимной связи, – описательно или количественно.
   
2. 
   В каком виде представлены данные – сгруппированном или несгруппированном.
   
3. 
   Требуется ли измерить связь между двумя явлениями или между несколькими.
   

Наиболее простыми для расчета и широко используемыми являются:

• 
  коэффициент линейной корреляции (r_ху);
  
• 
  коэффициент ранговой корреляции (р);
  
• 
  коэффициент ассоциации (Q).
  

Коэффициент линейной корреляции является наиболее точным. Его используют:

• 
  при прямолинейной зависимости между изучаемыми явлениями (признаками);
  
• 
  небольшом числе наблюдении (число парных вариант не более 30);
  
• 
  несгруппированных данных.
  

Коэффициент ранговой корреляции применяют в том случае, когда не нужна большая точность оценки силы связи. Его используют:

• 
  при прямолинейной, криволинейной зависимости между изучаемыми явлениями или когда определить ее вид невозможно;
  
• 
  небольшом числе наблюдений (не больше 30);
  
• 
  при сравнении не только количественных, но и качественных (атрибутивных) признаков;
  
• 
  при измерении связи между альтернативными признаками, имеющими несколько градаций, т. е. при альтернативной догме;
  
• 
  когда в сравниваемых рядах величин имеются открытые группы, не имеющие четких границ (например, в ряду величин, характеризующих стаж работы, могут быть группы: «до 5 лет», «более 20 лет»).
  

Коэффициент ассоциации является наиболее точным и находит применение для измерения связи между альтернативными признаками.

Названные коэффициенты рассчитываются по следующим формулам:

Линейной корреляции	Ранговой корреляции	Ассоциации
где: rху – коэффициент корреляции Х и У – числовые значения сравниваемых явлений признаков dх и dу – отклонения каждого значения ряда «х» или ряда «у» от средней величины данного ряда  – знак суммы	где: рxy – коэффициент корреляции рангов n – число парных членов коррелируемых рядов (х и у) d – разность между порядковыми номерами парных членов рядов  – знак суммы	где: Q – коэффициент ассоциации а, в, с, d – обозначения каждого из 4-х сравниваемых показателей

Поскольку при измерении связи между явлениями, как правило, пользуются выборочными методами исследования, т. к. расчеты производятся на выборочных совокупностях, полученные коэффициенты нуждаются в подтверждении их достоверности. Для этого необходимо вычислить среднюю ошибку коэффициента корреляции.

Средняя ошибка (m) коэффициентов линейной и ранговой корреляции вычисляется по однотипной формуле:

для коэффициента линейной корреляции	для коэффициента ранговой корреляции
где: mr – средняя ошибка n – число пар r²ху – коэффициент линейной корреляции	где: mр – средняя ошибка n – число пар р²ху – коэффициент ранговой корреляции

Средняя ошибка коэффициента ассоциации определяется по формуле:

,

где Q – коэффициент ассоциации

Достоверность коэффициентов корреляционной связи определяется с помощью критерия достоверности – t, который вычисляется путем деления величины показателя на величину рассчитанной для него средней ошибки:

или или

• 
  Коэффициенты корреляционной связи считаются достоверными, если они в 3 (три) раза превышают свою среднюю ошибку;
  
• 
  При малом числе наблюдений значение критерия достоверности, рассчитанное для конкретного коэффициента, сравнивается с критериями в специальной таблице, соответствующими числу наблюдений в данном исследовании (см. табл. 7 и 8).
  

Коэффициент корреляции (r_ху) одним числом измеряет силу связи между изучаемыми явлениями и дает представление о ее направлении;

• 
  По направлению связь может быть прямой и обратной.
  

Прямой (положительной) связью называется такая связь, когда оба явления изменяются в одном направлении. Например, с ухудшением питания ухудшаются показатели здоровья населения.

Обратной (отрицательной) связью называется связь, когда одно явление увеличивается, а другое при этом уменьшается. Например, с понижением температуры воздуха в осенне-зимний период частота простудных заболеваний увеличивается.

Коэффициент корреляции, характеризующий прямую связь, обозначается знаком плюс (+), а обратную связь – знаком минус (–).

• 
  По силе связи коэффициенты корреляции колеблются от единицы (полная функциональная связь) до нуля (отсутствие связи). Промежуточные значения (1r0) говорят о наличие связи более или менее сильной степени. Чем больше среднему значению одного признака соответствует значений другого признака, тем выше сила связи между ними. Оценка размеров корреляции может производиться по следующей схеме.