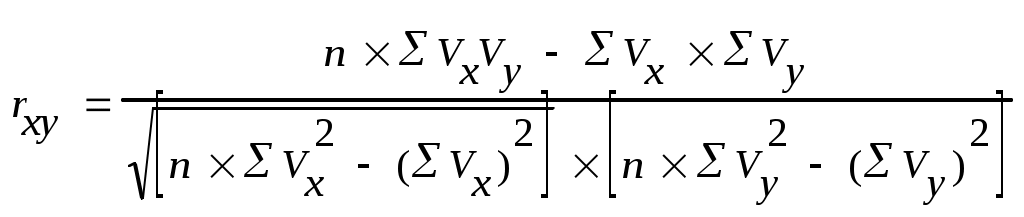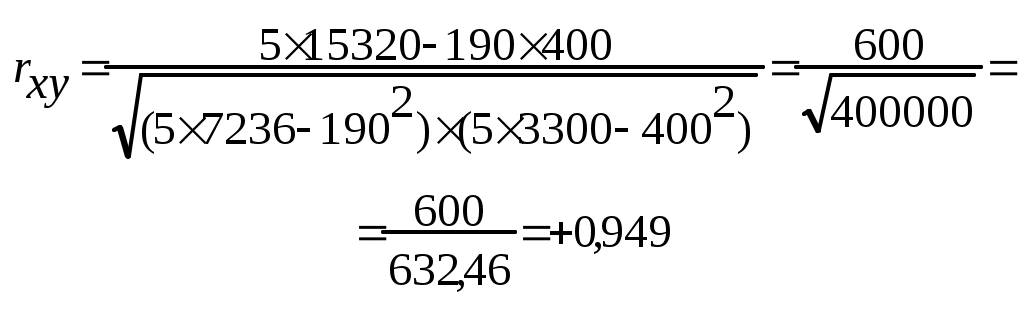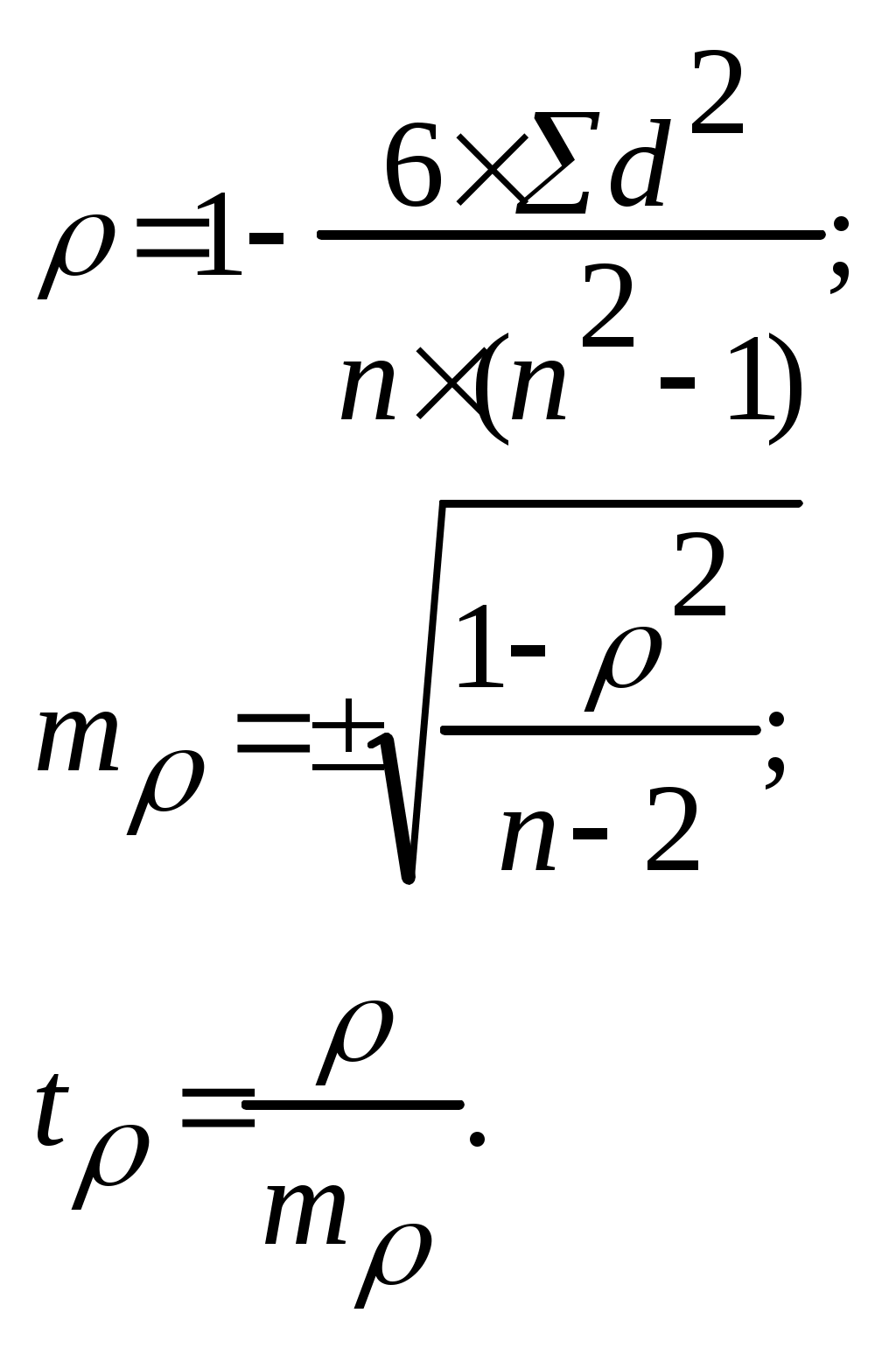Учебное пособие управляющего типа Агарков В. И., Бутева Л. В. Грищенко С. В. Донецк Донгму, 2006. 277 с

Название	Учебное пособие управляющего типа Агарков В. И., Бутева Л. В. Грищенко С. В. Донецк Донгму, 2006. 277 с
Дата	24.03.2023
Размер	3.03 Mb.
Формат файла
Имя файла	Posobie_po_med_statistike.doc
Тип	Учебное пособие #1011845
страница	27 из 35

1 ... 23 24 25 26 27 28 29 30 ... 35

Схема оценки коэффициента корреляции

Сила связи	Величина коэффициента при наличии
Сила связи	прямой корреляции	обратной корреляции
Малая (низкая, слабая) Средняя Большая (высокая, сильная)	от 0 до +0,3 от 0,3 до +0,7 от 0,7 до +1,0	от 0 до –0,3 от –0,3 до –0,7 от –0,7 до –1,0

Таким образом, корреляционные коэффициенты своей величиной и знаком показывают степень или силу связи и ее направление.

Необходимо помнить о том, что вычисление коэффициентов корреляции целесообразно лишь в том случае, если специалисты, изучающие сущность какой-либо проблемы предполагают наличие связи между явлениями. А сама по себе статистика не решает вопрос о том, возможна ли связь между явлениями или нет.

МЕТОДИКА ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТА

ЛИНЕЙНОЙ КОРРЕЛЯЦИИ
Для его вычисления следует пользоваться алгоритмом, приведенным в табл. 4 и правилами, перечисленными ниже.

Таблица 4

Алгоритмы расчета коэффициента линейной корреляции (r_ху), его ошибки (m_r) и коэффициента достоверности (t_r)

V_x	V_у	d_x (X-M_x)	d_ү (Y-M_y)	d_x×d_ү	d_х²	d_у²	Формулы
1	2	3	4	5	6	7	8

ΣV_x	ΣV_y
				Σd_x×d_ү	Σd_x²	Σd_y²

Записать исходные данные в виде двух вариационных рядов (графы 1 и 2)
Найти суммы вариант в каждом вариационном ряду (х и у) и определить средние арифметические величины (М_х и М_у) – графы 1 и 2.
Найти d_x и d_у – отклонения каждой варианты от средних величин (графы 3 и 4).
Полученные отклонения перемножить попарно (d_х × d_у) и найти сумму полученных произведений (d_х × d_у) – графа 5.
Каждое отклонение в обоих рядах возвести в квадрат и определить сумму квадратов отклонений ряда V_х (графа 6) и ряда V_у (графа 7).
Определить произведение d²_х × d²_у и из произведения извлечь квадратный корень d²_х × d²_у
Подставить полученные данные в формулу и рассчитать коэффициент корреляции (R_ху) – графа 8.
Подставить необходимые данные в формулу и рассчитать среднюю ошибку (m_r) коэффициента корреляции – графа 8.
Подставить необходимые данные в формулу и рассчитать коэффициент достоверности (t_r) – графа 8.

При наличии вычислительной техники расчет коэффициента линейной корреляции производится по следующей схеме (табл.5.)

Таблица 5

Алгоритм расчета (на ЭВМ) коэффициента корреляции (R_ху)

Vx	Vy	Vx ∙ Vy	Vx²	Vy²	Формула

åVx	Vy	Vx×Vy	Vx²	Vy²

Для примера вычислим коэффициент корреляции между температурой тела и частотой пульса в минуту у 5 больных (табл. 6). Для этого воспользуемся алгоритмами, приведенными в табл. 4 и 5.

Таблица 6

Пример определения r_ху между температурой

тела и частотой пульса в минуту

Температура тела(˚C), х	Частота пульса (удары в минуту), y	d_x (X-M_x)	d_ү (Y-M_y)	d_x×d_ү	d_х²	d_у²
36	60	-2	-20	40	4	400
36	70	-2	-10	20	4	100
38	80	0	0	0	0	0
40	90	+2	+10	20	4	100
40	100	+2	+20	40	4	400
∑x=190	∑y=400

Подставим полученные данные в формулу и рассчитаем коэффициент корреляции:

Рассчитаем среднюю ошибку (m_r) коэффициента достоверности:

Рассчитаем коэффициент достоверности t_r:

Оценим критерий t_r по специальным таблицам (табл. 7 и 8), в которой слева показано число наблюдений (n), а сверху – степень вероятности безошибочного прогноза (р).

Таблица 7

Значение критерия t_r для трех степеней вероятности

(по Н.А. Плохинскому)

p n	95%	99%	99,9%	p n	95%	99%	99,9%
1	12,7	63,7	37,0	10	2,2	3,2	4,6
2	4,3	9,9	31,6	11	2,2	3,1	4,4
3	3,2	5,8	12,9	12	2,2	3,1	4,3
4	2,8	4,6	8,6	13	2,2	3,0	4,1
5	2,6	4,0	6,9	14-15	2,1	3,0	4,1
6	2,4	3,7	6,0	16-17	2,1	2,9	4,0
7	2,4	3,5	5,3	18-20	2,1	2,9	3,9
8	2,3	3,4	5,0	21-24	2,1	2,8	3,8
9	2,3	3,3	4,8	25-29	2,0	2,8	3,7

Таблица 8

Стандартные коэффициенты корреляции, которые считаются достоверными (по Л.С. Каменскому)

Число степеней свободы, n′ (n – 2)	Уровень вероятности Р (в %)			Число степеней свободы, n′ (n – 2)	Уровень вероятности Р (в %)
Число степеней свободы, n′ (n – 2)	95,0	98,0	99,0	Число степеней свободы, n′ (n – 2)	95,0	98,0	99,0
1	0,997	0,999	0,999	12	0,532	0,612	0,661
2	0,950	0,980	0,990	13	0,514	0,592	0,641
3	0,878	0,934	0,959	14	0,497	0,574	0,623
4	0,811	0,882	0,917	15	0,482	0,558	0,606
5	0,754	0,833	0,874	16	0,468	0,542	0,590
6	0,707	0,789	0,834	17	0,456	0,528	0,575
7	0,666	0,750	0,798	18	0,444	0,516	0,561
8	0,632	0,716	0,765	19	0,433	0,503	0,549
9	0,602	0,685	0,735	20	0,423	0,492	0,537
10	0,576	0,658	0,708	25	0,381	0,445	0,487
11	0,553	0,634	0,684	30	0,349	0,409	0,449

Вывод. Коэффициент корреляции, равный 0,949, достоверен с вероятностью безошибочного прогноза р>95%, так как при n=3 (5 – 2) полученный нами критерий t будет больше t_табл.=3,2 (р=95%) и меньше t_табл.=5,8 (р=99%). Материалы выборочного исследования позволяют утверждать, что в генеральной совокупности существует сильная прямая связь между температурой тела и частотой пульса.

Оценка достоверности коэффициента корреляции может осуществляется по специальной таблице (при малых выборках) без предварительных расчетов m и t. Необходимо лишь сравнить r_ху со стандартным коэффициентом корреляции, рассчитанным и представленным в таблице для различной степени вероятности и различного числа наблюдений (см. табл. 8).

По данным оценки достоверности полученного коэффициента корреляции с помощью приведенной выше таблицы можно говорить о том, что коэффициент, равный 0,949, достоверен с вероятностью безошибочного прогноза р>98%, так как при n=3, он больше 0,934 и меньше 0,959.

При наличии вычислительной техники расчет коэффициента корреляции производится по следующей схеме (табл. 9)

Таблица 9

Пример определения r_ху

(с помощью вычислительной техники)

между температурой тела и частотой пульса в минуту

№ п/п	Vx	Vy	Vx×Vy	Vx²	Vy²	Расчет по формуле
1	36	60	2160	1296	3600
2	36	70	2520	1296	4900
3	38	80	3040	1444	6400
4	40	90	3600	1600	8100
5	40	100	4000	1600	10000
	190	400	15320	7236	33000

Вывод. Между температурой тела и частотой пульса имеется прямая и сильная связь.

МЕТОДИКА ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТА

РАНГОВОЙ КОРРЕЛЯЦИИ

Последовательность расчета коэффициента ранговой корреляции отражена в табл. 10 и правилах, перечисленных после алгоритма.

Таблица 10

Алгоритм расчета коэффициента ранговой корреляции (р), его ошибки (m_p) и коэффициента достоверности (t_p)

Признак x	Признак y	Порядковые номера (ранги) для рядов		Разность между рангами (d=x′–y′)	Квадрат разности (d²)	Формулы для расчета
Признак x	Признак y	х′	y′	Разность между рангами (d=x′–y′)	Квадрат разности (d²)	Формулы для расчета
1	2	3	4	5	6	7

					∑d²

Составить ряды из парных признаков (графы 1 и 2).
Каждую величину признака заменить ранговым (порядковым) номером – х′ и у′. (в тех случаях, когда имеется несколько одинаковых по величине чисел, порядковый номер обозначают средним числом из суммы очередных порядковых их номеров). Ранжировать значения обоих рядов в строго определенном направлении от меньшей величины к большей или от большей к меньшей (графы 3 и 4).
Определить разность между рангами для каждой пары членов ряда (по каждой строке) – графа 5.
Возвести в квадрат каждое из полученных значений разности между рангами и определить сумму квадратов разности рангов (d²) – графа 6.
Подставить полученные данные в формулу и рассчитать коэффициент корреляции рангов – графа 7.
Подставить необходимые данные в формулу и рассчитать среднюю ошибку (m_p) коэффициента ранговой корреляции – графа 7.
Подставить необходимые данные в формулу и рассчитать коэффициент достоверности (t_p) – графа 7.

Методику расчета и оценки коэффициента корреляции рангов разберем на следующем примере (см. табл. 11).

Таблица 11

Данные о заболеваемости дифтерией жителей городов

Н-ской области и о выполнении плана профилактических прививок в отчетном году

Города	Заболеваемость дифтерией (на 100 чел.)	Выполнение плана профпрививок (в %)	Ранги		Разность рангов	Квадрат разности рангов
	х	у	Х₁	У₁	d (х-у)	d²
А	3,29	86	1	8	7	49
Б	3,21	82	2	10	8	64
В	3,17	88	3	7	4	16
Г	2,85	84	4	9	5	25
Д	2,84	90	5	6	1	1
Е	2,71	95	6	4	2	4
Ж	2,23	100	7	1	6	36
З	1,82	92	8	5	3	9
И	1,80	98	9	2	7	49
К	0,70	96	10	3	7	49
						∑d²=302

Подставим полученные данные в формулу и рассчитываем коэффициент ранговой корреляции:

Рассчитаем среднюю ошибку (m_p):

Рассчитаем коэффициент достоверности:

Условием достоверности коэффициента корреляции рангов, как, впрочем, и всех остальных коэффициентов корреляционной зависимости, является превышение коэффициента своей утроенной ошибки:

Таким образом, –0,833×0,197 или –0,83>0,591 т.е. полученные результаты достоверны.

Вывод. Полученный коэффициент корреляции рангов статистически достоверен. Следовательно, можно говорить о сильной, обратной связи между заболеваемостью дифтерией и процентом выполнения плана профилактических прививок. Заболеваемость выше в тех городах, где план профилактических прививок выполнен недостаточно.

При вычислении коэффициента корреляции по методу рангов бывают случаи, когда отдельные показатели ряда встречаются несколько раз. В этом случае порядковый номер каждого из них (ранг) определяется как средняя из сумм очередных порядковых номеров. Например, надо поставить порядковые номера (ранги) показателей возраста 10 студентов:

Возраст

(годы), Х

Ранги по величине показателей возраста проставляются следующим образом: возраст 21 год, его порядковый номер = 1. возраст 22 года встречается дважды, занимая по своей величине 2-е и 3-е места, поэтому порядковые номера в данном случае будут равны полусумме занимаемых этим возрастом мест – (2+3):2=2,5, т.е. против каждого показателя возраста 22 года будет поставлен порядковый номер (ранг) 2,5. возраст 23 года встречается 3 раза, занимая 4-е, 5-е и 6-е места соответственно, т.к. 2-е и 3-е места использованы для возраста 22 года. Ранги для возраста 23 года будут равны – (4+5+6):3=5, т.е. против каждого возраста 23 года необходимо поставить порядковый номер (ранг) 5. в целом ранги показателей возраста у студентов будут следующие:

Возраст (годы), Х	22	22	21	24	23	23	24	23	24	24
Ранги	2,5	2,5	1	7,5	5	5	7,5	5	7,5	7,5

МЕТОДИКА ВЫЧИСЛЕНИЯ

КОЭФФИЦИЕНТА АССОЦИАЦИИ
Последовательность расчета коэффициента ассоциации отражена ниже.

Алгоритм расчета коэффициента ассоциации (Q),

его ошибки (m_a) и коэффициента достоверности (t_a).

Построить четырехпольную таблицу. В первом столбце этой таблицы наносят обе разновидности одного явления – Х₁ и Х₂, а в первой строке – обе разновидности второго – У₁ и У₂.При этом Х₁ и У₂ обозначают положительные разновидности (например, выздоровевшие, иммунизированные и т. д.), а Х₂ и У₂– отрицательные (например, не выздоровевшие, не иммунизированные). Обозначить через буквы а, в, с, d четыре поля, в которые внести исходные данные:

Y Х	Y₁ Заболело	Y₂ Не заболело
Х₁ Вакцинировано	а	в
Х₂ Невакцинировано	с	d

2. Вычислить произведения аd и вс.

3. Подставить полученные данные в формулу

и рассчитать коэффициент ассоциации.

П одставить необходимые данные в формулу и рассчитать среднюю ошибку коэффициента ассоциации.
Подставить необходимые данные в формулу и рассчитать коэффициент достоверности.

Методику расчета и оценки коэффициента ассоциации разберем на следующем примере.

Необходимо определить, влияет ли вакцинация против гриппа на заболеваемость от этой инфекции. Известно, что на промышленном предприятии с общей численностью в 2000 человек 1200 рабочим были сделаны прививки против гриппа, а 800 рабочих остались не привитыми. Заболело из привитых 240 человек, а из непривитых – 320.

Данные о заболевших и не заболевших среди привитых и не привитых приведены в табл. 12.

Таблица 12

Распределение заболевших и не заболевших среди

привитых на промышленном предприятии

	Заболело	Не заболело	Всего
Привитых	240	960	1200
Не привитых	320	480	800
Всего	560	1440	2000

Вычислим произведения аd и вс:

a×d=240×480=11520

b×c=960×320=307200

Подставим полученные данные в формулу и рассчитаем коэффициент ассоциации:

Рассчитаем среднюю ошибку (m_Q):

Рассчитаем коэффициент достоверности:

Таким образом, –0,453×0,0740,222. Коэффициент статистически достоверен, что означает, что существует обратная, средней силы связи между заболеваемостью гриппом и вакцинацией против него.

Задания для коррекции умений

Изучив теоретические вопросы темы, приступайте к решению задач, которые помогут Вам в отработке умений, первая из которых направлена на решение вопроса о возможности наличия связи между явлениями.

1 ... 23 24 25 26 27 28 29 30 ... 35