Урганч давлат университети

• Название: Урганч давлат университети
• Дата: 18.06.2022
• Размер: 1.76 Mb.
• Имя файла: O‘zbеkiston rеspublikasi (1).doc
• Тип: Документы; #601147
• страница: 5 из 11

2. Эконометрик моделлар сифати ва аҳамиятини мезонлар бўйича баҳолаш.
Аппроксимация хатолиги



(1)


n - кузатувлар сони

y - асосий омилни ҳақиқий қийматлари

ŷ - асосий омилни текисланган қийматлари

Аппроксимация хатолиги 10% гача қабул қилинади.

Фишернинг мезони ⁶. Инглиз статистиги Фишер корреляцион ва регрессион таҳлилларнинг ишончлилигини текшириш учун логарифмик функциядан фойдаланиш усулини ишлаб чиқди:

. (2)

тақсимот кичик танламада нормал тақсимотга яқин бўлади. Ф.Миллс ва да ( -бош тўпламда корреляция коэффициенти) ва тақсимот графигини ўтказади. нинг ўртача квадратик хатоси қуйидаги формула бўйича аниқланади:

. (3)

Ушбу формулада ўртача квадратик хато фақат тақсимот ҳажмига, яъни тақсимоти боғланиш зичлигига боғлиқ бўлмайди. дан га ўтиш тегишли жадваллар бўйича амалга оширилади ҳамда корреляцион ва регрессион таҳлил натижалари ишончлилигини текшириш унча қийин бўлмайди.

Фишер мезони ёрдамида тўлиқ моделни адекватлигини, яъни реал иқтисодий жараёнга мослигини текшириш мумкин:




(4)
n- кузатувлар сони

m - моделдаги таъсир этувчи омиллар сони

R- кўп омилли корреляция коэффициенти.

Ҳисобланган Фишер мезони жадвалдаги қиймати билан солиштирилади. Жадвалдаги Фишер коэффициентини топиш учун k1 катор ва k2 устунни аниқлаш зарур k1=n-m-1 ва k2=m. Агар

модел аҳамиятли, яъни регрессия тенгламаси тури тўғри аниқланган деб ҳисобланади.

Стьюдентнинг мезони. Мазкур мезон Стьюдент тахаллусли инглиз математиги Уильям Госсет томонидан ишлаб чиқилган.

Стьюдентнинг тақсимоти кичик танламалар учун махсус белгиланган. тақсимот тақсимлагичли суратга эга бўлган қиймат муносабатларида, кейинчалик арифметик ўртача қиймат тақсимлашда учрайди

, (5)

бу ерда, - бош ўртача;

- эркинлик даражаси сони ;

- тегишли танлама тўплам арифметик ўртача қиймати ва ўртача квадратик четланиши.

Жуфт корреляция коэффициентини текшириш учун эркинлик даражасини тақсимотга эга бўлган формула орқали қиймати аниқланади.

Агар бўлса, нолинчи гипотезани қўллаб бўлмайди ва бинобарин бош тўпламда чизиқли корреляция мавжуд. Унинг ишончли таърифи сифатида корреляциянинг чизиқли коэффициенти намоён бўлади.

Жуфт корреляция коэффициентини текшириш учун эркинлик даражасини тақсимотга эга бўлган формула орқали қиймати аниқланади.

Агар бўлса, нолинчи гипотезани қўллаб бўлмайди ва бинобарин бош тўпламда чизиқли корреляция мавжуд. Унинг ишончли таърифи сифатида корреляциянинг чизиқли коэффициенти намоён бўлади. Чизиқсиз боғланишда тўплам корреляциясининг индекси ишончлилиги ҳам худди шу усулда текширилади. Бундай ҳолда (4) формуладаги корреляция коэффициенти корреляция индекси билан алмаштирилади. Тўплам корреляция коэффициенти квадратик хатога эга

, (6)

бу ерда, -регрессия коэффициентлари сони.

Шундай қилиб, мезоннинг эмпирик қиймати қуйидаги формула бўйича аниқланади:

, (7)

бу ерда, - эркинлик даражалари сони;

- жадвалдаги қиймати билан солиштирилади;

- эркин даражалари билан тақсимотга эга бўлган

, (8)

қиймати асосида регрессия коэффициентларининг ишончлиги текширилади.

Эконометрик моделларни таҳлил қилаётганда даражалар тебранувчанлиги икки жиҳатдан қаралиши мумкин. Биринчидан, улар ўрганилаётган жараён ёки ҳодисаларнинг ривожланиш қонуниятлари намоён бўлиши учун ҳалақит қиладиган «тасодифий тўсиқлар» ёки «ахборот шовқинлари» сифатида талқин этилади. Шу сабабли даражаларни улардан «тозалаш», яъни тасодифий тўсиқларни динамиканинг жузъий томонлари сифатида бартараф қилиш ёки жуда бўлмаганда таъсир кучини заифлаштириш йўлларини топиш ва илмий асослаш зарурияти туғилади.
Дарбин – Уотсон мезони

Автокорреляция- бу кейинги даражалар билан олдингилари ўртасидаги ёки ҳақиқий даражалари билан тегишли текисланган қийматлари ўртасидаги фарқлар орасидаги корреляциядир.

Ҳозирги вақтда автокорреляция мавжудлигини текширишда Дарбин – Уотсон мезони қўлланади: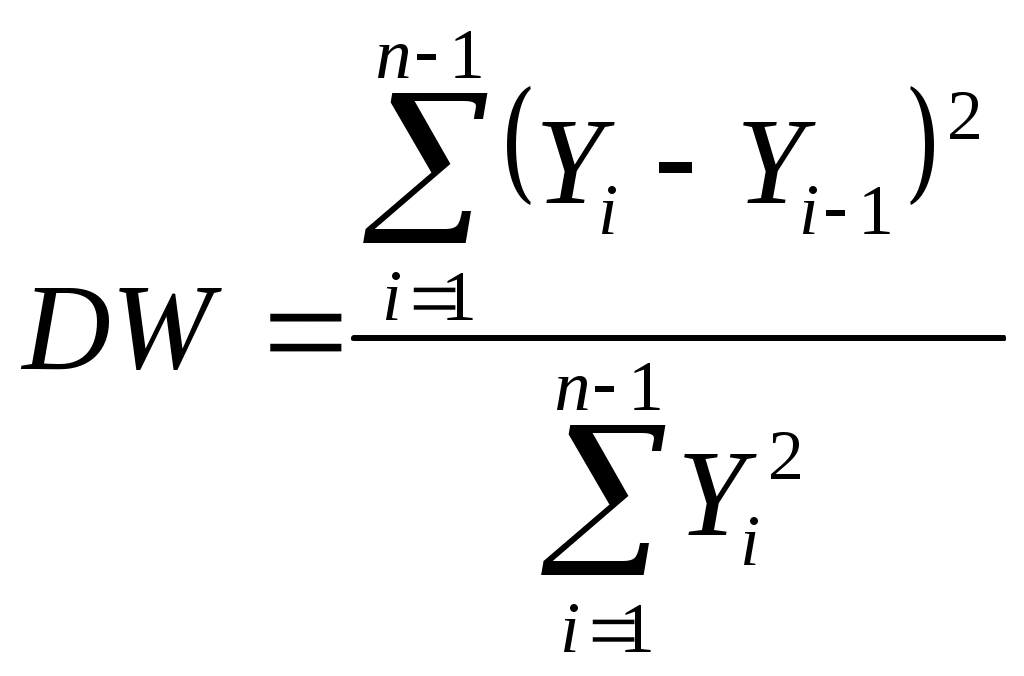

(9)

DW мезоннинг мумкин бўлган қийматлари 0–4 оралиқда ётади. Агар қаторда автокорреляция бўлмаса, унинг қийматлари 2 атрофида тебранади. Ҳисоблаб топилган ҳақиқий қийматлари жадвалдаги критик қиймат билан таққосланади. Агарда DW_ҳақDW_паст бўлса, қатор автокорреляцияга эга; Д_ҳақDW_юқори бўлса у автокорреляцияга эга эмас; DW_пастDW_ҳақDW_юқори бўлса, текширишни давом эттириш лозим. Бу ерда DW_паст ва DW_юқори – мезоннинг қуйи ва юқори чегаралари. Салбий автокорреляция мавжуд (минус ишорага эга) бўлса, у ҳолда мезон қийматлари 2–4 орасида ётади, демак, текшириш учун DW4- DW қийматларини аниқлаш керак

Вақтли қаторларнинг кейинги ва олдинги ҳадлари ўртасидаги корреляцион боғланиш ҳисобланади. Автокорреляциянинг мавжулиги қаторлар динамикаси даражаларининг ўзаро болиқлигидан, кейинги ҳадларнинг олдинги ҳадларга кучли даражада болиқлигидан далолат беради. Чунки корреляцион таҳлил усулини ўзаро боғланган ҳар бир қатор даражаси статистик мустақилликка эга бўлган, ўрганилаётган қаторлар динамикасида автокорреляция мавжудлигини аниқлаш лозим бўлган ҳоллардагина тадбиқ етиш мумкин. Автокорреляция мавжудлигини текшириш жараёни қуйидагича амалга оширилади. r_а (ҳисоб) қиймати ҳисобланади:

(10)
Бунда: z_t - қолдиқ миқдор;

Агар ҳисоблаб топилган r_а (ҳисоб) миқдор берилган бир процентли хатолар эҳтимоллиги ва эркинлик даража сонлари N - n- 1 бўлганда тегишли r_а (жад) (r_а (жад)<r_а (ҳисоб)) қийматидан катта бўлса, автокорреляция бўлмайди. Сўнгра ишончлилик интерваллари аниқланади. У коэффитциентлар вариацияси ёрдамида қуйидаги формула асосида аниқланади.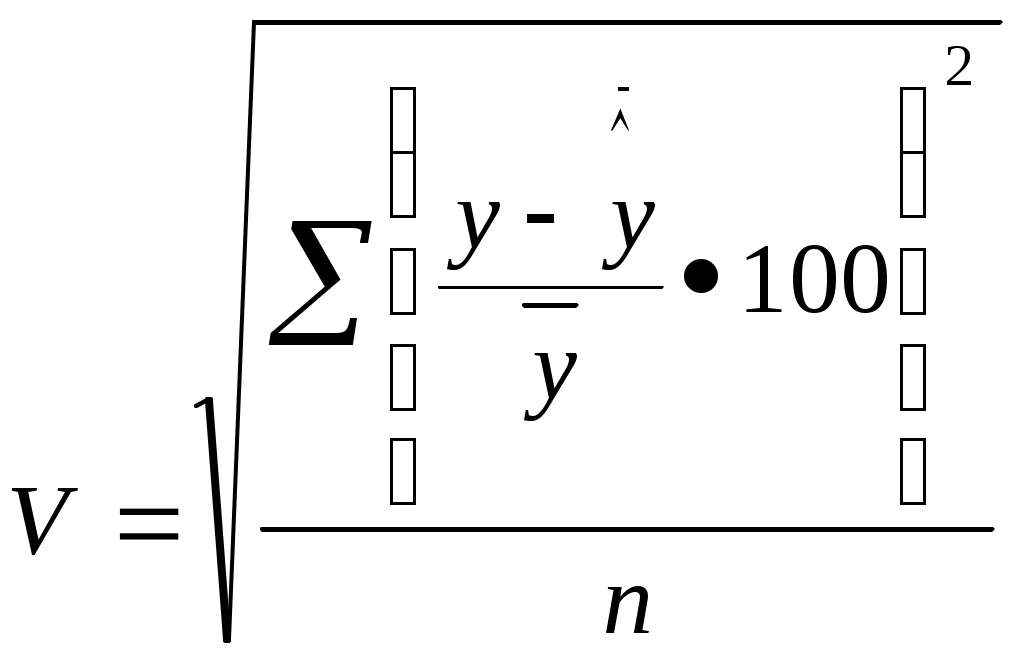

(11)
Бунда: y назарий қаторлар динамикасининг ўртача қиймати. Шундан сўнг қуйи интервали y_i (1-VG’100) юқори интервал бўйича yi(1QVG’100) ишонч интерваллари ҳисоблаб чиқилади.

Қуйидаги ҳолатлар корреляцион таҳлил усулини башоратлашда қўллашда хатоликларга олиб келиши мумкин:

а) башоратлаштирилаётган ҳодиса кўрсаткичлари динамикасини аниқлашда муҳим аҳамиятга эга бўлган факторлар имконини ола билмаслиги;

б) корреляцион тенгламалар коэффитциентлари уларнинг қийматини аниқлайдиган шароитлар ўзгариши билан қийматининг ўзгарувчанлиги;

в) бир қиймат ўзгаришининг башорати бошқа бир қанча қийматлар ўзгариш қиймати билан алмаштирилади.
3. Гомоскедатлик ва гетероскедатликни аниқлаш учун тестлар.
“Энг кичик квадратлар” усулининг эконометрик моделлардаги параметрларни баҳолашда қолдиқлар квадратлари йиғиндисининг минимумга интилишига асосланади. Шунинг учун регрессиянинг қолдиқ қийматларини кўриб чиқиш муҳим аҳмият касб этади.

“Энг кичик квадратларининг” учинчи тахмини гомоскедатликка тегишли бўлиб, у ҳар бир Х учун қолдиқнинг дисперсияси бир хил бўлиши эканлигини англатади. Бу тахмин, масалан Х нинг катта қийматлари учун қолдиқ дисперсиясини имкони, ҳудди кичик қийматлардаги каби деган тасдиқ билан келишилади.

Гомоскедатлик шарти:

Агар юқоридаги “Энг кичик квадратлар” усулининг қўлланиш шарти бажарилмаса, бунда гетероскедатлик ҳолати ҳосил бўлади. Гетероскедатлик регрессия тенгламасининг параметрлари самарадорлигини пасайишига таъсир қилмоқда.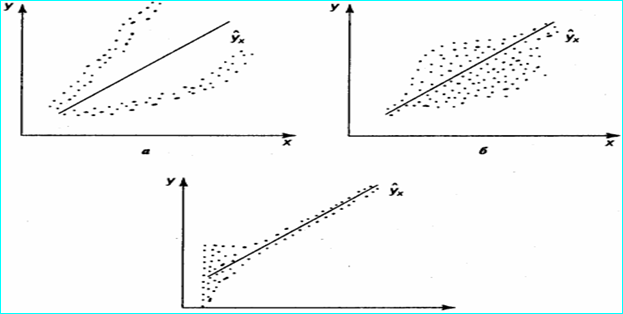


4. Эконометрик моделлардаги параметрларни иқтисодий жиҳатдан баҳолаш мезонлар
Чизиқли бир омилли модел қуришда унинг айрим камчиликларига эътиборни қаратмоқ лозим. Моделни жараённинг битта омил ёрдамида, у ҳатто ҳал қилувчи омил бўлган тақдирда ҳам ҳаққоний ёритиб бериш мумкин емас. Масалан, пахта хом ашёсини ялпи йиғиб олишни ўрганишда асосий омил сифатида ҳосилдорликни олиш мумкин, лекин синчиклаб ўрганиш натижасида ер миқдори ва сифати, ўғитлар (уларни миқдори, сифати, қуритиш муддати), суғориш харакат тартиби ва бошқа омилларни ҳам эътиборга олиш зарур.

Шундай қилиб, «асосий» омиллар миқдори чексиз ўзгариши мумкин. Бундай масаларни ҳалэ этиш бир омилли моделдан кўп омиллигача ўтишни тақозо этади. Аммо бу ҳам функцияга асосий омиллардан ташқари яна кўп сонли иккинчи даражали омиллар таъсир қилиши ҳисобига ҳисоблашда ҳатолик бўлишини рад этмайди. Кўпинча уларнинг таъсири сезиларсиз ва қарама-қарши характерга эга. Ушбу омилларнинг барча самараси, ҳам мусбат ҳам манфий қийматларни қабул қилувчи «У» тасодифий ўзгарувчи билан баҳоланади. Чизиқли боғлиқлик:

ёки , кўринишда бўлади.

«У» ўзгарувчи қуйидаги стохастик хусусиятларга эга бўлган ҳато сифатида намоён бўлади:

-эҳтимолий меъёрий тақсимотга эга бўлади;

-нолли ўртачага эга;

-чекли дисперсияга эга;

-ўлчаш ҳатоси ҳисобланади.

Статистик маълумот йиғишда кўп ҳолларда параметрнинг ҳақиқий қийматлари ўрнига яширин ҳатога эга ўлчамлар киритилади (улар объктив, субъектив характерга эга бўлишлари, ўлчам ҳисобларининг ноаниқлиги, ноаниқ ҳужжат айланиши, алоҳида ўлчамларини субъектив бахоси ва бошқалар). Барча юқорида санаб ўтилган камчиликлар ўлчаш ҳатоларини тенглама ҳатоларига ўтишига олиб келади, яъни⁷:

(12)

бунда W-жами ҳато; У-стохастик эътироз билдириш; В-ўлчаш ҳатоси.

Нисбатан оддий боғлиқлик деб чизиқли бир омилли боғлиқлик ёки чизиқли кўп омилли модел, у тасодифий ҳатога нисбатан бир неча тахминларни қабул қилганда ҳисобланади: ўртача нолга тенг; дисперcия cуст ва асосий омилларга боғлиқ эмас ва тасодий ҳато бир-бирига боғлиқ эмас.

Кўп омилли ҳолатда: , а₀ ва а₁ коэффитциентларни қуйидаги шартлардан келиб чиққан ҳолда аниқлаш мумкин:



(13)
Содда иқтисодий моделларни кўриб чиқишда бу масалани стандарт усули ёрдамида ечиш мумкин. Энг кичик квадрат усули классик ҳисобланади. Лекин нисбатан мураккаброқ вазиятларда мураккаб эонометрик моделни кўриб чиқишда мураккаб техника йўллардан фойдаланган холда янги усулларни ишлаб чиқиш зарур.

Оддий чизиқли регрессион моделнинг тўлиқ спетсификацияси регрессион тенгламадан ва 5 та бирламчи йўл қўйишлардан ташкил топган.

Шу йўл қўйишларни кўриб чиқамиз. Биринчи икки тахмин шундан иборатки, Х нинг хар бир қиймати учун  ҳато нол қиймат атрофида меъёрий тақсимланган. Тахмин қилинадики, _i узлуксиз катталик ҳисобланиб,ўртача атрофида симметрик тақсимланган дан гача ўзгаради ва унинг тақсимланиши 2 ўлчам ўртача ва вариатсия ёрдамида аниқланади.

Демак:

Биринчи тахмин: _i - меъёрий тақсимланган.

Иккинчи тахмин: - ўртача ҳато нолга тенг.

Ҳақиқатда биз стохастик ҳатони ҳар бир қийматини, кўпгина сабаблар натижаси сифатида кўришимиз мумкинки, бунда ҳар бир сабаб боғлиқ ўзгарувчини, у детерминистик ҳисобланиши мумкин бўлган қийматдан сезиларсиз тарзда оғдиради.

Бундай кўздан кечиришда ўлчаш ҳатоси ўхшаши билан тақсимот ҳатоси тўғри ва шунинг учун ўртача ҳатони меъёрийлигини ва нолга тенглиги ҳақида тахминлар ўхшаш.

Учинчи тахмин гомоскедикликка тегишли бўлиб, у ҳар бир ҳато ² нинг қиймати номаълум бўлган бир хил вариатсияга эканлигини англатади. Бу тахмин, масалан Х нинг катта қийматлари учун ҳато дисперсиясини имкони, ҳудди кичик қийматлардаги каби деган тасдиқ билан келишилади. Юқорида кўриб ўтилган ишлаб чиқариш функсиясида, бу тахминга асосан ишлаб чиқаришдаги вариатсия ҳам, иш кучи қийматига боғлиқ эас.

Учинчи тахмин: Гомоскедиклик:

. (14)

Тўртинчи тахмин: қолдиқдаги автокорреляция билан боғлиқ. Тахмин қилинадики, ҳатолар орасида автокорреляция йўқ, яъни автокорреляция мавжуд эмас:

(15)

Бу тахмин шуни англатадики, агар бугун натижадаги ишлаб чиқариш кутилгандан кўп бўлса, бундан эртага ишлаб чиқариш кўп (ёки кам) бўлади деган хулосага келиш керак эмас.

Биринчи ва тўртинчи тахмин биргаликда эҳтимоллик нуқтаи-назаридан, тақсимот ҳатолари боғлиқ емас дейиш имконини беради. Шунинг учун ₁, ₂,..._n ўзгарувчини ўхшаш ва эркин тақсимланиши сифатида қаралиши мумкин. Е(_i)=0 бўлгани учун

. (16)

Бундан

(17)

Бешинчи таҳмин: Х эркин ўзгарувчи стохастик эмаслигини тасдиқлайди. Бошқача қилиб айтганда, Х нинг қийматлари назорат қилинади ёки бутунлай башорат қилинади.Бу тахминни муҳим қўлланилиши шундан иборатки, i ва j нинг барча қийматлари учун

(18)

Бешинчи тахмин: Х қийматлари стохастик эмас, улар танлашда танлов миқёсидан қатъий назар ўхшаш

, (19)

нолдан фарқ қилади ва унинг n лимити чекли сон.

Тўғри, амалиётда кўрсатилган тахминларни мутлоқ мавжудлигига аниқ эришиш қийин, лекин биз агар бу тахминларга тахминан амал қилинса қониқиш ҳосил қиламиз. Юқорида келтириб ўтилган тахминлар классик чизиқли регрессион модел тузиш, Регресия параметларини ҳисоблаш учун зарур.

Регрессион тенглама ва беш тахмин билан келтирилган регрессион моделнинг тўлиқ спетсификатсиясидан сўнг, энди уни айрим ўзига ҳос томонларини кўриб чиқамиз. Авваломбор,  боғлиқ ўзгарувчининг тақсимот эҳтимолига қайтамиз.

_i функсиянинг биринчи ўртачаси, (8) тенгламанинг икки қисмини математик кутилиши сифатида олиниши мумкин:

(20)

Бу,  ва  параметрлар спетсификатсиясидан, Х_i нинг стохастик емаслигидан (бу берилган сон ) ва ўртачадан (иккинчи тахмин) келиб чиқади.

Кейин Y_i вариатсия бўлмиш

(21)

Ҳар бир Х боғлиқ ўзгарувчига  ўзгарувчини ўртача қийматини берувчи тенглама регрессиянинг емпирик чизиғи дейилади.

Бу чизиқни ордината билан кесишиши, Х нинг нолга тенг қийматида  баҳосини ўлчайдиган  катталикка мос келади.  нинг оғиши,  қийматни Х қийматнинг ҳар бир қўшимча бирлигига оғишдаги ўзгаришини ўлчайди. Масалан, агар  ялпи истеъмол, Х ялпи даромад кўринишида бўлса, у ҳолда  нолга тенг даромадда истеъмол даражасининг чегаравий оғишини намоён қилади. Бу ўлчамлар қийматлари номаълум бўлгани учун регрессиянинг емпирик чизиғи маълум емас.  ва  нинг ўлчамлари қийматларини ҳисоблаб, регрессиянинг назарий чизиғини оламиз.  ва  нинг қийматлари ҳисоблангандек мос ҳисобланган бўлса, мос холда, бунда регрессиянинг назарий чизиғи қуйидаги тенглама орқали берилган :

(22)

бунда -  нинг текисланган қиймати.

Барчаси бўлмаса ҳам, кўпчилиги  емпирик қийматлар назарий чизиқда ётмайди, шунинг учун i ва қийматлар мос келмайди. Бу фарқ қолдиқ деб аталади ва билан белгиланади. Шунинг учун қуйидаги тенгламалар фарқланади:

(эмпирик)

(назарий).