Урганч давлат университети
 Скачать 1.76 Mb. Скачать 1.76 Mb.
|
|
Қисқа хулосалар. Ҳодисалар орасидаги ўзаро боғланишларни ўрганиш эконометрика фанининг муҳим вазифасидир. Бу жараёнда икки хил белгилар ёки кўрсаткичлар иштирок этади, бири эркли ўзгарувчилар, иккинчиси эрксиз ўзгарувчилар ҳисобланади. Иқтисодий жараёнларни моделлаштиришда ва башорат қилишда иқтисодий статистиканинг усулларидан кўп фойдаланилади. Иқтисодий-статистик усуллар динамик жараёнларга нисбатан, яъни вақт бўйича ўзгарувчи жараёнларга қўлланилади. Иқтисодий-статистик усуллар ёрдамида иқтисодий ўзгарувчилар орасидаги боғланиш зичликларини, уларни акс эттирувчи моделларни олиш мумкин. Ўзгарувчи белгининг миқдорлари мажмуаси вариатсион қатор дейилади. Агар вариантлар кўпайиш ёки камайиш бўйича жойлаштирилса, тартибли вариатсион қатор ҳосил бўлади. Иқтисодий-статистик моделлаштириш иқтисодий кўрсаткичлар ва ишлаб чиқариш омиллари ўртасидаги алоқалар ўз моҳиятига кўра стохастик бўлган асосга таянади. Иқтисодий субъектлар фаолиятини статистик моделлаштириш замон ва маконда уларнинг ривожланиш жараёнини ўрганишда асосий ўрин эгаллайди. Бу моделлар ишлаб чиқариш тенденсиялари ва қонуниятларини аниқлаш учун мослашгандир. Мустақил ўрганиш учун саволлар 1. Иқтисодий кўрсаткичларни қандай шаклларда намоён этиш мумкин? 2. Иқтисодий маълумотларни қайта ишлашнинг қандай усулларини биласиз? 3. Талаб ва таклиф моделида қайси ўзгарувчи боғлиқ ва қайси ўзгарувчи боғлиқ эмас? 4. Эконометрик моделларни тузишда қандай талаблар қўйилади? 5. Омиллар ўлчов бирлигини танлашда қандай муаммоларга дуч келинади? 6. Эконометрик моделларнинг қандай шакллари мавжуд? 7. Эконометрик моделларда уч ва ундан ортиқ омиллар қанаша оладими? 8. Вақтли қаторлар деганда нимани тушунасиз? 9. Тўғри чизиқ тенгламасининг иқтисодий моҳиятини тушунтириб беринг. 10. Қайси ҳолларда чизиқсиз моделлар тузилади? 3-мавзу. Жуфт корреляцион-регрессион таҳлил 1. Иқтисодий-ижтимоий жараёнларда боғликликлар турларини ўрганиш. 2. Корреляция коэффициентининг турлари ва ҳисоблаш усуллари. 3. Чизиқли ва чизиқсиз регрессион боғланишлар. 4. Корреляцион-регрессион таҳлилда энг кичик квадратлар усулининг қўлланилиши. 1. Иқтисодий-ижтимоий жараёнларда боғликликлар турларини ўрганиш. Ижтимоий-иқтисодий жараёнлар ўртасидаги ўзаро боғланишларни ўрганиш эконометрика фанининг муҳим вазифаларидан биридир. Бу жараёнда икки хил белгилар ёки кўрсаткичлар иштирок этади, бири боғлиқ бўлмаган ўзгарувчилар, иккинчиси боғлиқ ўзгарувчилар ҳисобланади. Биринчи турдаги белгилар бошқаларига таъсир этади, уларнинг ўзгаришига сабабчи бўлади. шунинг учун улар омил белгилар деб юритилади, иккинчи тоифадагилар эса натижавий белгилар дейилади. Масалан, истеъмолчининг даромади ортиб бориши натижасида унинг товар ва хизматларга бўлган талаби ошади. Бу боғланишда талабнинг ортиши натижавий белги, унга таъсир этувчи омил, яъни даромад эса омил белгидир. Омилларнинг ҳар бир қийматига турли шароитларида натижавий белгининг ҳар хил қийматлари мос келадиган боғланиш корреляцион боғланиш ёки муносабат дейилади. Корреляцион боғланишнинг характерли хусусияти шундан иборатки, бунда омилларнинг тўлиқ сони номаълумдир. Шунинг учун бундай боғланишлар тўлиқсиз ҳисобланади ва уларни формулалар орқали тақрибан ифодалаш мумкин, холос. Корреляция сўзи лотинча correlation сўзидан олинган бўлиб, ўзаро муносабат, мувофиқлик, боғлиқлик деган маънога эга. Икки ҳодиса ёки омил ва натижавий белгилар орасидаги боғланиш жуфт корреляция деб аталади. Корреляцион боғланишларни ўрганишда икки тоифадаги масалалар кўндаланг бўлади. Улардан бири ўрганилаётган ҳодисалар (белгилар) орасида қанчалик зич (яъни кучли ёки кучсиз) боғланиш мавжудлигини баҳолашдан иборат. Бу корреляцион таҳлил деб аталувчи усулнинг вазифаси ҳисобланади. Коррреляцион таҳлил деб ҳодисалар орасидаги боғланиш зичлик даражасини баҳолашга айтилади. Омилларнинг узаро богланиши 2 турга булинади: функционал богланиш ва корреляцион богланиш. Йуналишларнинг ўзгаришига караб, боғланишлар икки турга бўлинади: тўгри боғланиш ва тескари боғланишлар. Аналитик ифодаларнинг кўринишларига қараб ҳам боғланишлар икки турга бўлинади: тўғри чизиқли ва чизиксиз боғланишлар. Фукционал боғланишларда бир ўзгарувчи белгининг ҳар қайси қийматига бошқа ўзгарувчи белгининг аник битта қиймати мос келади. 2. Корреляция коэффициентининг турлари ва ҳисоблаш усуллари. Корреляцион таҳлил корреляция коэффициентларини аниқлаш ва уларнинг муҳимлигини, ишончлилигини баҳолашга асосланади. Чизиқли корреляция коэффициентининг ҳисоблаш формуласи 3: бу ерда, Детерминатсия коэффициенти корреляция коэффициентининг квадратига тенг. Корреляция коэффициенти (r) –1 дан +1 оралиғида бўлади. Агар Боғланиш зичлик даражаси одатда қуйидагича талқин этилади. Агар Корреляцион тахлил ўтказилганда қуйидаги корреляция коэффициентлари ҳисобланади: 1. Хусусий корреляция коэффициентлари. Хусусий корреляция коэффициенти асосий ва унга таъсир этувчи омиллар ўртасидаги боғланиш зичлигини билдиради. 2. Жуфт корреляция коэффициентлари асосий омил инобатга олинмаган нуқтада ҳисобланади. Агар жуфт корреляция коэффициенти 0,6 дан катта бўлса, унда омиллараро боғланиш кучли деб ҳисобланади ва эркин омиллар маълум даражада бир бирини такрорлайди. Агар моделда ўзаро боғланган омиллар қатнашса, модел ёрдамида қилинган ҳисоблар нотўғри чиқиши мумкин ва омиллар таъсири икки баровар ҳисобланиши мумкин. Ўзаро боғланган таъсир этувчи омиллардан биттаси моделдан чиқариб ташланади. Албатта моделда кучлироқ ва мустаҳкамроқ омил қолади. 3. Кўп омилли моделларда агар натижавий омилга бир неча омиллар таъсир кўрсатса, унда омиллар орасида кўпликдаги корреляция коэффициенти ҳисобланади. Ижтимоий-иқтисодий жараёнлар ўртасида боғланишларни ўрганишда қуйидаги функциялардан фойдаланилади 3. Чизиқли ва чизиқсиз регрессион боғланишлар. Ижтимоий-иқтисодий жараёнлар ўртасида боғланишларни ўрганишда қуйидаги функциялар билан фойдаланилади: Чизиқли – Иккинчи даражали парабола – Учинчи даражали парабола – n-даражали парабола – Гипербола – b- даражали гипербола – Логарифмик – Ярим логарифмик – Кўрсаткичли функция – Даражали функция – Логистик функция – Боғланишлар чизиқли бўлса, у ҳолда боғланиш зичлиги баҳолашда корреляция коэффициентидан фойдаланиш мумкин: бу ерда, 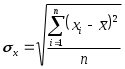 , , 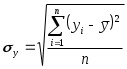 Шунингдек, корреляция коэффициентини ҳисоблашнинг қуйидаги модификацияланган формулаларидан ҳам фойдаланиш мумкин: 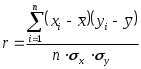 ёки ёки 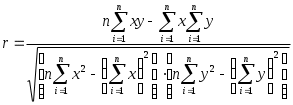 . .Регрессион таҳлил натижавий белгига таъсир этувчи омилларнинг самарадорлигини аниқлаб беради. Регрессия сўзи лотинча regressio сўзидан олинган бўлиб, орқага ҳаракатланиш деган маънога эга. Бу атама корреляцион таҳлил асосчилари Ф.Гальтон ва К.Пирсон номлари билан боғлиқдир. Регрессион таҳлил натижавий белгига таъсир этувчи белгиларнинг самарадорлигини амалий жиҳатдан етарли даражада аниқлик билан баҳолаш имконини беради. Регрессион таҳлил ёрдамида ижтимоий-иқтисодий жараёнларнинг келгуси даврлар учун башорат қийматларини баҳолаш ва уларнинг эҳтимол чегараларини аниқлаш мумкин. Регрессион ва корреляцион таҳлилда боғланишнинг регрессия тенгламаси аниқланади ва у маълум эҳтимол (ишончлилик даражаси) билан баҳоланади, сўнгра иқтисодий-статистик таҳлил қилинади. 4. Корреляцион-регрессион таҳлилда энг кичик квадратлар усулининг қўлланилиши. Регрессион моделнинг параметрларини баҳолаш боғлиқ ўзгарувчи Y нинг тақсимланиш эҳтимолини топишдир. Моделда Yi нормал тақсимланган ва вариацияси var (Y)=2 га тенг. Энг кичик квадратлар усулида ҳисоблаш тамойили Yi ларнинг хақиқий қийматларининг ўртача қийматидан фарқининг квадрати суммасини топишдан иборат. Демак: ёки бу ерда, S - фарқлар квадратлари суммаси4. ва , қийматларини топиш учун S нинг ва бўйича биринчи хосиласини топамиз: Ҳар бир хосилани нолга тенглаштириб ҳисоблаб топилган ёки бунга эквивалент равишда Бу тенгламалар энг кичик квадратлар усулида нормал тенгламалар деб аталади. Бунда е энг кичик квадратлар қолдиғи: () тенглама 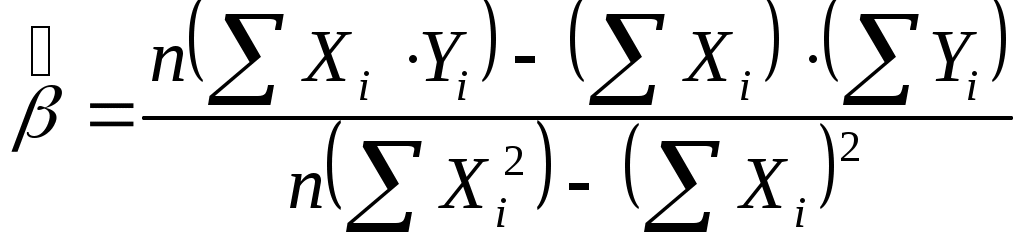 Бу тенгликни бошқача кўринишда ҳам ёзиш мумкин: 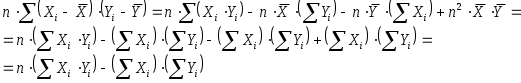 Демак 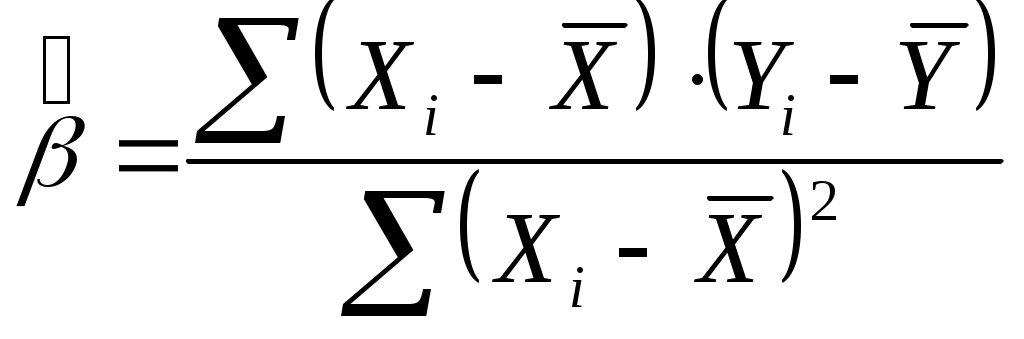 Регрессия тенгламасини ҳисоблаш. Оддий регрессия моделини ҳисоблаш. Қуйидаги жадвалда келтирилган маълумотлар асосида регрессия тенгламаси ҳисобланасин. Бу ерда Y - истеъмол ҳаражатлари; Х - Шахсий даромад.
Т=15; = 4310,4/15=287,36 (Х-Х)=Х-ТХ=1504576-15(309,86)=64378 (Y-Y)=Y-TY=1294309-15(287,36)=55672=SST (X-X)(Y-Y)=XY-TXY==1395464-15(309,86)(287,36)=59843 Y-X=287,36-(0,92956)(309,86)=0,6735 SSR= SSE=SST-SSR=55672-55627=45 R= F=(T-2)R/(1-R)=13 t=F=127,4 S=SSE/(T-2)=45/13=3,46 Y=-0,6735+0,92956X=(127,4) R=0,9992 F=16237 T=15 (Y-Y)=Y-TY=1294309-15(287,36)=55672 SST=(X-X)(Y-Y)=XY-TXY=1395464-16(309,86)(287,36)=59843 = =Y-X=287,36-(0,92956)(309,86)=0,6735 SSR= SSE=SST-SSR=55672=45 R= F=(T-2)R/(1-R)=13 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
