Урганч давлат университети

• Название: Урганч давлат университети
• Дата: 18.06.2022
• Размер: 1.76 Mb.
• Имя файла: O‘zbеkiston rеspublikasi (1).doc
• Тип: Документы; #601147
• страница: 7 из 11

Ўртача сирғалувчи усул - бу қатор даражаларини бирин-кетин маълум тартибда суриш йўли билан ҳисобланган ўртача даражадир. Ўртача сирғалувчи усулда қатор кўрсаткичларидан доимо тенг сонда олиб, улардан оддий арифметик ўртача ҳисоблаш йўли билан аниқланади. Уларни тоқ ёки жуфт сонда олинадиган қатор кўрсаткичлари асосида ҳисобалаш мумкин.

Ўртача сирғалувчи усул ўртача қийматни аниқлаш вақтида тасодифий четланишларнинг ўсиш ҳолатига асосланади. Ўртача фактик қийматлар қаторлари динамикаси текисланаётган вақтда сирғанишнинг ўртача нуқта даврини кўрсатадиган ўртача қийматлар билан алмашинади. Одатда ўртача сирғанувчи усулнинг икки модификациясидан, яъни оддий ва вазнли текислашдан фойдаланилади.

Оддий тенглаштириш ўрталикдаги 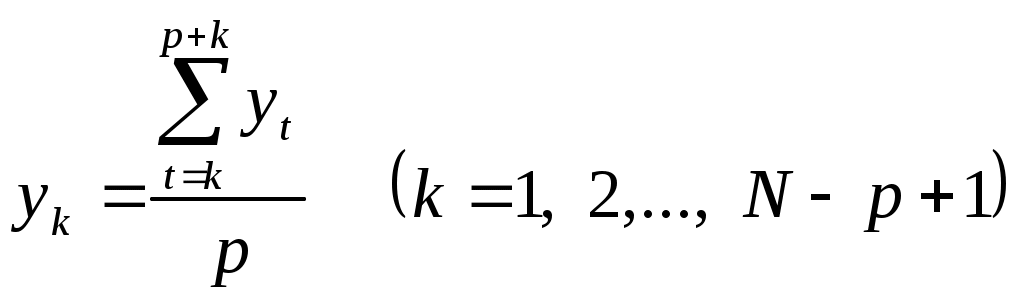узунликдаги вақт учун оддий ўрта арифметик ҳисоблашдан тузилган янги қатор тузишга асосланади:

, (17)

бу ерда, – тенглаштириш даври узунлиги вақтли қаторлар характерига боғлиқ бўлади;

– ўртача қийматнинг тартиб номери.

Вазнли тенглаштириш турли нуқтадаги қаторлар динамикаси учун вазнли ўртача қийматларни ўртачалаштиришдан иборат.

Биринчи қаторлар динамикасини олиб кўрайлик ( одатда 1 ёки 2 га тенг). Тенденциялар функцияси сифатида қандайдир:

(18)

(18) тўла даражасини олайлик.

Унинг параметрлари

(19)

тенгламаси ёрдамида энг кичик квадратлар усули билан аниқланади.

Кўпҳад (полином) ўртача даражаси нуқтасига жойлашган. га нисбатан тенгламани ечсак:

(20)

ҳосил қиламиз. Бу ердаги қиймати ва моҳиятига боғлиқ бўлади. Ҳосил бўлган тенглама (4) биринчилардан қаторлар динамикаси қийматининг вазнли ўртача қиймат арифметикаси ҳисобланади.

Экспоненсиал усули ҳозирги пайтда, динамик қаторларга асосланган усуллардан энг муҳим усул деб ҳисобланади. Динамик қаторларни башоратлашда маълумотларни йилдан йилга ўзгартиришини эътиборга олиш зарур. Оҳирги йиллардаги ўзгариш тенденциясини аҳамиятини ошириб, динамик қаторни биринчи йиллардаги ўзгариш тенденциясини аҳамиятини камайтириш зарур.

Башоратлаштиришнинг оддий моделларидан бири бўлган вақтли функциясини кўриб ўтамиз. Умумий ҳолда вақт бўйича олинган функциясини

у_т = f (t) (21)

(22)

кўринишида ифодалаш мумкин.

Айрим ҳолларда вақтли қатор параметрлари маълум бир оралиқда ўзгариши мумкин.

Бу муаммони ечиш учун Браун томонидан яратилган экспоненсиал усулидан фойдаланамиз. Бу усулни моҳияти шундан иборатки, вақт бўйича олинган қатор экспоненсиал қонуниятига бўйсуниб башорат қилинади.

Фараз қилайлик:

(23)

кўринишидаги чизиқли функция берилган бўлсин. Бу ердаги а₀ ва а₁ параметрларни топиш учун ўртача экспоненсиал ва миқдорларни топамиз.

(24)

(25)

Агар бу системани а₀ ва а₁ га нисбатан ечсак, қуйидагиларни хосил қиламиз:

(26)

(27)

К даражадаги экспонента рекурент формуласи орқали топилади.

(28)

Бу йерда  = 2 / m + 1

m -кузатувлар сони.

Умуман олганда 0   1 бўлади.

Агар  параметр 1 га яқин бўлса, башоратлаштириш учун кейинги ҳолатлар ҳисобга олинади. Агар а 0 бўлса башоратда илгари ҳолат назарда тутилади.
Қисқа хулосалар.

Ижтимоий-иқтисодий ҳодисаларнинг вақт давомида ўзгариши динамика деб, шу жараённи таърифловчи кўрсаткичлар қатори эса вақтли қаторлари деб юритилади.

Ҳодисаларнинг вақт давомида ўзгаришини таърифловчи статистик кўрсаткичлар қатори вақтли қатор деб юритилади.

Вақтли қаторлар икки элементдан таркиб топади: бири вақт моментлари ёки даврлар, иккинчиси - уларга тегишли кўрсаткичлар.

Вақтли қаторлар узоқ муддатли тенденция, айрим даврларга хос циклик ёки локал ўзгаришлар, кундалик тебранишлар ва мавсумий ўзгаришларни ўзида мужассамлаштириши мумкин. Динамика тенденциясини аниқлашнинг энг содда усули қатор даражалари даврини узайтириш усулидир. Бу усулда кетма-кет жойлашган қатор даражалари тенг сонда олиб қўшилади, натижада узунроқ даврларга тегишли даражалардан тузилган янги ихчамлашган қатор ҳосил бўлади.

Ўртача сирғалувчи усул - бу қатор даражаларини бирин-кетин маълум тартибда суриш йўли билан ҳисобланган ўртача даражадир. Ўртача сирғалувчи усулда қатор кўрсаткичларидан доимо тенг сонда олиб, улардан оддий арифметик ўртача ҳисоблаш йўли билан аниқланади. Уларни тоқ ёки жуфт сонда олинадиган қатор кўрсаткичлари асосида ҳисобалаш мумкин.

Ўртача сирғалувчи усул ўртача қийматни аниқлаш вақтида тасодифий четланишларнинг ўсиш ҳолатига асосланади. Ўртача фактик қийматлар қаторлари динамикаси текисланаётган вақтда сирғанишнинг ўртача нуқта даврини кўрсатадиган ўртача қийматлар билан алмашинади. Одатда ўртача сирғанувчи усулнинг икки модификациясидан, яъни оддий ва вазнли текислашдан фойдаланилади.

Мустақил ишлаш учун назорат саволлари:

1. 
   Вақтли қатор деб нимага айтилади?
   
2. 
   Вақтли қаторлар вариацион қаторлардан қандай хусусиятлари ва аломатлари билан фарқ қиладилар?
   
3. 
   Вақтли қаторларни қандай усуллар билан текислаш мумкин?
   
4. 
   Ўртача сирғалувчан усул нима ва қачон қўлланади?
   
5. 
   Автокорреляция нима ва у қандай таҳлил қилинади?
   
6. 
   Мультиколлениеарлик нима ва у корреляцион боғланиш натижаларига қандай таъсир этади ҳамда қайси йўл билан уни бартараф қилиш мумкин?
   
7. 
   Вақтли қаторларда корреляцион-регрессион таҳлил усулларини қўллаш шарт-шароитларини тушунтириб беринг?
   
8. 
   Таклиф ва бошқа бозор иқтисодиёт қонунлари намоён бўлишини ўрганишда регрессион таҳлил усулларидан фойдаланиш тартибини мисолларда тушунтириб беринг.
   
9. 
   Бозор нархига нисбатан таклиф эластиклигини аниқлаш мақсадида регрессион таҳлил усулидан фойдаланиш тартибини аниқ бир мисолда тушунтириб беринг.
   
10. 
    Энг кичик квадратлар усулининг моҳиятини тушунтириб беринг.
    

7-мавзу. Тенгламалар тизими кўринишидаги эконометрик модел
1.Бир-бирига боғлиқ тенгламалар тизимини тушунчалари ва турлари.

2.Эконометрик тенгламлар тизими параметрларини ҳисоблаш услубиёти.

3.Эконометрик тенгламалар тизимини индентификациялаш муаммолари.
1.Бир-бирига боғлиқ тенгламалар тизимини тушунчалари ва турлари.
Одатда иқтисодий кўрсаткичлар ўзаро боғланган бўлишади. Бундай кўрсаткичлар (ўзгарувчилар) ўртасидаги муносабатлар таркиби бир вақтли тенгламалар тизими ёрдамида кўрсатилиши мумкин. Мазкур тенгламаларда қуйидаги турдаги ўзгарувчилар мавжуд бўлади:

- эндоген, тизим ичида аниқланувчи, боғлиқли у ўзгарувчилар;

- экзоген, қиймати ташқаридан бериладиган, бошқариладиган, башоратланувчи, таъсир этувчи х ўзгарувчилар;

- олдиндан белгиланган ўзгарувчилар, хам жорий вақтдаги экзоген ўзгарувчиларни, хам лаг ўзгарувчилар (ўтган даврлар учун экзоген ва эндоген ўзгарувчилар)ни ўз ичига оладиган.

Эконометрик тизимларнинг қуйидаги турлари ажратилади.

Боғлиқ бўлмаган тенгламалар тизими, бунда хар бир боғлиқ ўзгарувчи y_i(i=1,…,n), боғлиқ бўлмаган бир хил тўплам ўзгарувчилар x_j (j=1,…,m)ларнинг функцияси сифатида берилади:

y₁ = a₁₁ x₁ + a₁₂ x₂ + …+a_1m x_m + ₁

y₂ = a₂₁ x₁ + a₂₂ x₂ + …+a_2m x_m + ₂ (1)

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

y_n = a_n1 x₁ + a_n2 x₂ + …+a_nm x_m + _n

Мазкур тизимининг хар бир тенгламасини регрессия тенгламаси сифатида мустақил қаралиши мумкин. Унга озод ҳадлар киритилиши мумкин ва регрессия коэффицентлари энг кичик квадратлар (ЭКК) усули ёрдамида топилиши мумкин.

Рекурсив тенгламалар тизими, бунда боғлиқ ўзгарувчилар y_i(i=1,…,n), боғлиқ бўлмаган ўзгарувчилар x_j (j=1,…,m)ларнинг ва олдин аниқланган боғлиқ ўзгарувчилар y₁ , y₂ ,…, y_i-1ларнинг функцияси сифатида кўрсатилади:

y₁ = a₁₁ x₁ + a₁₂ x₂ + …+a_1m x_m + ₁

y₂ = b₂₁ y₁ + a₂₁ x₁ + a₂₂ x₂ + …+a_2m x_m + ₂ (2)

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

y_n = b_n1 y₁ + b_n2 y₂ +,…,+b_nn-1 y_n-1 +a_n1 x₁ + a_n2 x₂ + …+a_nm x_m + _n

Тизимнинг хар бир тенгламаси параметрлари, энг кичик квадратлар усули ёрдамида, биринчи тенгламадан бошлаб, кетма кет аниқланади.

Ўзаро боғлиқ тенгламалар тизими, бунда хар бир боғлиқ ўзгарувчи y_i (i=2,…,n) бошқа боғлиқ ўзгарувчилар y_k (k  i) ва боғлиқ бўлмаган ўзгарувчилар x_j (j=1,…,m)нинг функцияси сифатида келтирилган:
y₁= b₁₂ y₂ + b₁₃ y₃ + …+ b_1n y_n +a₁₁ x₁ + a₁₂ x₂ + …+a_1m x_m + ₁

y₂= b₂₁ y₁ + b₂₃ y₃ + …+ b_2n y_n +a₂₁ x₁ + a₂₂ x₂ + …+a_2m x_m + ₂ (3)

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

y_n= b_n1 y₁ + b_n2 y₂ + …+ b_nn-1 y_n-1 +a_n1 x₁ + a_n2 x₂ + …+a_nm x_m + _n
Бу тизим энг кўп тарқалган бўлиб, бирлашган, бир вақтли тенгламалар тизими номи билан аталади. Уни таркибий модел шакли (ТМШ) деб хам аташади.

ТМШ ўзгарувчиларнинг баъзи коэффицентлари нольга тенг бўлиши мумкин, бу ҳолат мазкур ўзгарувчиларнинг тенгламада мавжуд бўлмаслигини билдиради. Масалан, нарх ва иш ҳақи динамикаси модели ТМШ кўринишида ёритилиши мумкин:

y₁= b₁₂ y₂ +a₁₁ x₁ + ₁

y₂= b₂₁ y₁ + a₂₂ x₂ +a₂₃ x₃ + ₂ (4)

бунда y₁–иш ҳақи ўзгариши темпи;

y₂ – нархлар ўзгариши темпи;

x₁ – ишсизлар фоизи;

x₂– доимий капитал ўзгариши темпи;

x₃ – хом ашё импорти нархларининг ўзгариш темпи.

Иккита тенгламадан ташкил топган мазкур тизим иккита боғлиқ, эндоген (y₁ , y₂) ва учта боғлиқ бўлмаган, экзоген (x₁,x₂,x₃) ўзгарувчилардан иборат. Биринчи тенгламада x₂ ва x₃ ўзгарувчилари мавжуд эмас. Бу коэффицентлар a₁₂= 0ва a₁₃= 0 эканлигини билдиради.

2.Эконометрик тенгламлар тизими параметрларини ҳисоблаш услубиёти.
Эконометрик тенгламлар тизими параметрларини юкорида келтирилган “Энг кичик квадратлар” усули ёрдамида хисоблаш мумкин.

Эконометрик тизимлар бўйича прогнозлаш учун кетма-кет бир нечта босқичлардан ўтиш лозим:

1. Берилган маълумотлар асосида корреляцион таҳлил ўтказилади:

а) хусусий корреляция коэффициентлар матрицаси ҳисобланади;

б) жуфт корреляция коэффициентлари матрицаси ҳисобланади.

2. Корреляцион таҳлил натижасида танланган омиллар асосида регрессия тенгламаси қурилади;

3. Қурилган тенгламалар тизими қуйидаги мезонлар бўйича баҳоланади⁹:

а) Фишер мезони;

б) Стьюдент мезони;

в) Дарбин-Уотсон мезони;

г) Кўплик корреляция коэффициенти;

д) Детерминация коэффициенти;

е) аппроксимация хатолиги.

4. Қурилган тенгламалар тизими мезонларга мос келса, кейин асосий кўрсаткич тенглама асосида прогноз даври ҳисобланади.

5. Ишлаб чиқариш функциясини асосий хусусиятлари қуйидагилар ҳисобланади:

а) ўртача унумдорлик омиллари;

б) чегаравий унумдорлик омиллари;

в) ресурслар бўйича эластиклик коэффициентлари;

г) ресурсларга талаб;

д) ресурсларни алмаштириш чегаралари.

Таркибий моделни коэффициентларини баҳолашда бир қатор усуллар қўлланилади.

Аниқ идентификацияланадиган таркибий моделда қўлланадиган билвосита энг кичик квадратлар усулини (БЭКК) кўриб чиқамиз. Мазкур усулини иккита эндоген ва иккита экзоген кўрсаткичлардан иборат бўлган қуйидаги идентификацияланадиган модел мисолида кўриб чиқамиз:

y₁= b₁₂ y₂ + a₁₁ x₁ + ₁ (5)

y₂= b₂₁ y₁ + a₂₂ x₂ + ₂

Моделни тузиш учун 1-жадвалда келтирилган маълумотлар билан фойдаланамиз.
1 -жадвал

Ҳақиқий маълумотлар

n	У1	у2	х1	х2
1	33,0	37,1	3	11
2	45,9	49,3	7	16
3	42,2	41,6	7	9
4	51,4	45,9	10	9
5	49,0	37,4	10	1
6	49,3	52,3	8	16
Сумма	270,8	263,6	45	62
Ўртача қиймат	45,133	43,930	7,500	10,333

Таркибий моделни келтирилган шаклига тубдан ўзгартирамиз:

y₁= d₁₁ x₁ + d₁₂ x₂ + u₁

y₂= d₂₁ x₁ + d₂₂ x₂ + u₂

u₁ ва u₁ – тасодифий ҳатолар.

Ҳар бир келтирилган шаклдаги тенгламаси учун d коэффициентларини ҳисоблашда ЭКК усули қўлланилиши мумкин.

Ҳисоблашларни осонлаштириш учун ўртача даражадан y=y-y_cp ва x=x-x_cp (y_cpва x_cp –ўртачалар) четланишлар билан фойдаланса бўлади. Тубдан ўзгартирилган 1-жадвалдаги маълумотлар 2-жадвалга тортилган. Шу ерда d_ik коэффициентларни аниқлаш учун керакли оралиқ ҳисоботлар келтирилган. Биринчи келтирилган тенгламанинг d_ik коэффициентларини аниқлаш учун қуйидаги нормал тенгламалар тизимини ишлатиш мумкин:

Σ y₁x₁= d₁₁ Σ x₁² + d₁₂ Σ x₁x₂

Σ y₁x₂= d₁₁ Σ x₁x₂ + d₁₂ Σ x₂²

5–жадвалда ҳисобланган сумма қийматларини ўрнига қўйиб чиқиб, қуйидагини оламиз:

83,102= 33,5 d₁₁ - 29,001d₁₂

-20,667= -29,001d₁₁ + 155,334d₁₂

Юқоридаги тенгламаларнинг ечилиши қуйидаги қийматларни беради d₁₁ = 2,822 и d₁₂ = 0,394.

2 -жадвал

Келтирилган модел шаклини тузиш учун ўзгартирилган маълумотлар

n	у1	у2	х1	х2	у1*х1	х12	х1*х2	У1*х2	у2*х1	у2*х2	х22
1	-12,133	-6,784	-4,500	0,667	54,599	20,250	-3,002	-8,093	30,528	-4,525	0,445
2	0,767	5,329	-0,500	5,667	-0,383	0,250	-2,834	4,347	-2,664	30,198	32,115
3	-2,933	-2,308	-0,500	-1,333	1,467	0,250	0,667	3,910	1,154	3,077	1,777
4	6,267	1,969	2,500	-1,333	15,668	6,250	-3,333	-8,354	4,922	-2,625	1,777
5	3,867	-6,541	2,500	-9,333	9,667	6,250	-23,333	-36,091	-16,353	61,048	87,105
6	4,167	8,337	0,500	5,667	2,084	0,250	2,834	23,614	4,168	47,244	32,115
Сумма	0,002	0,001	0,000	0,002	83,102	33,500	-29,001	-20,667	21,755	134,417	155,334

Келтирилган шаклнинг биринчи тенгламаси қуйидаги кўринишга эга бўлади:

y₁= 2,822 x₁ + 0,394 x₂ + u₁

Иккинчи келтирилган тенгламанинг d_2kкоэффициентларини аниқлаш учун қуйидаги нормал тенгламалар тизимини ишлатиш мумкин:

Σ y₂x₁= d₂₁ Σ x₁² + d₂₂ Σ x₁x₂

Σ y₂x₂= d₂₁ Σ x₁x₂ + d₂₂ Σ x₂²

2–жадвалда ҳисобланган сумма қийматларини ўрнига қўйиб чиқиб, қуйидагини оламиз:

21,755 = 33,5 d₂₁ - 29,001d₂₂

134,417= -29,001d₂₁ + 155,334d₂₂

Юқоридаги тенгламаларнинг ечилиши қуйидаги қийматларни беради d₂₁ =1,668 и d₂₂ =1,177.

Келтирилган шаклнинг иккинчи тенгламаси қуйидаги кўринишга эга бўлади:

y₂= 1,668 x₁ + 1,177 x₂ + u₂

Келтирилган шаклдан таркибли шаклга ўтиш учун келтирилган модел шаклнинг иккинчи тенгламасидан x₂ни топамиз:

x₂ = (y₂ - 1,668 x₁ ) / 1,177

Бу ифодани келтирилган моделнинг биринчи тенгламасига қўйиб чиқиб, таркибли тенгламани топамиз:

y₁= 2,822 x₁ + 0,394 (y₂ - 1,668 x₁ ) / 1,177 =

= 2,822 x₁ + 0,335 y₂ - 0,558 x₁ = 0,335 y₂ + 2,264 x₁

Шундай қилиб b₁₂ = 0,335; a₁₁ = 2,264.

Келтирилган модел шаклнинг биринчи тенгламасидан x₁ни топамиз:

x₁ = (y₁ - 0,394 x₂ ) / 2,822

Бу ифодани келтирилган моделнинг иккинчи тенгламасига қўйиб чиқиб, таркибли тенгламани топамиз:

y₂= 1,177 x₂ + 1,668 (y₁ - 0,394 x₂ ) / 2,822 =

= 1,177 x₂ + 0,591 y₁ - 0,233 x₂ = 0,591 y₁ + 0,944 x₂

Шундай қилиб b₂₁ = 0,591; a₂₂ = 0,944.

Таркибли шаклнинг озод ҳадларини қуйидаги тенгламалардан топамиз:

А₀₁= y_1,cp - b₁₂ y_2,cp - a₁₁ x_1,cp =45,133 – 0,335 * 43,93 –2,264* 7,5 = 13,436

А₀₂= y_2,cp -b₂₁ y_1,cp - a₂₂ x_2,cp=43,93 – 0,591* 45,133 - 0,944 * 10,333= 7,502

Сўнгги таркибли моделнинг кўриниши:

y₁= a₀₁+ b₁₂ y₂ + a₁₁ x₁ + ₁= 13,436 + 0,335 y₂ + 2,264 x₁ + ₁

y₂= a₀₂+ b₂₁ y₁ + a₂₂ x₂ + ₂= 7,502 + 0,591 y₁ + 0,944 x₂ + ₂