Урганч давлат университети
 Скачать 1.76 Mb. Скачать 1.76 Mb.
|
|
3.Эконометрик тенгламалар тизимини индентификациялаш муаммолари. ТМШда моделнинг таркибий коэффицентлари деб аталувчи, bij ва aij моделнинг параметрларини аниқлашда энг кичик квадратлар усули қўллана олинмайди. Одатда моделнинг таркибий коэффицентларини аниқлаш учун ТМШ келтирилган модел шаклига (КМШ) тубдан ўзгартирилади. y1 = 11 x1 + 12 x2 + …+1m xm y2 = 21 x1 + 22 x2+ …+2m xm (6) . . . . . . . . . . . . . . . . . . . . . . . . . . yn = n1 x1 + n2 x2 + …+nm xm КМШнинг ij параметрлари энг кичик квадратлар усулида баҳоланиши мумкин. Бу параметрлар орқали bij ва aij моделнинг таркибий коэффицентларини ҳисоблаб чиқиш мумкин. Таркибий ва келтирилган шаклларнинг параметрларини ўзаро мослигини таъминлаш учун идентификация шарти бажарилиши керак. Моделнинг таркибли шакли қуйидагича бўлиши мумкин: идентификацияланадиган; идентификацияланмайдиган; ўтаидентификацияланадиган. ТМШ идентификацияланадиган бўлиши учун, тизимнинг хар бир тенгламаси идентификацияланадиган бўлиши керак. Бу ҳолатда ТМШ параметрлари сони келтирилган форманинг параметрларига тенг бўлади. Агар ТМШнинг бирорта тенгламаси идентификацияланмайдиган бўлса, бунда бутун модель идентификацияланмайдиган бўлиб ҳисобланади.Бундай ҳолатда келтирилган шаклнинг коэффицентлари сони ТМШ коэффицентлари сонига нисбатан кам. Агар келтирилган коэффицентлар сони таркибли коэффицентларига нисбатан кўп бўлса, модель ўтаидентификацияланадиган деб ҳисобланади. Бунда келтирилган модел шаклининг коэффицентлари асосида бирор таркибий коэффициентининг икки ва ундан кўп қийматини топиш мумкин. Ўтаидентификацияланадиган моделда битта бўлса ҳам тенглама ўтаидентификацияланадиган, бошқалари эса идентификацияланадигандир. Агар, ТМШнинг i-тенгламасида эндоген ўзгарувчилар сонини Н орқали ва тизимда мавжуд бўлган, лекин ушбу тенгламага кирмайдиган олдиндан белгиланган ўзгарувчиларни D орқали белгиласак, моделнинг идентификация шарти қуйидаги ҳисоб қоидаси кўринишида ёзилиши мумкин: агар D+1 < H тенглама идентификацияланмайди; агар D+1 = H тенглама идентификацияланади; агар D+1 > H тенглама ўтаидентификацияланади. Идентификация учун мазкур қоида керакли, аммо етарли шарт эмас. Келтирлган қоидадан ташқари, тенглама идентификациясини аниқлаш учун кўшимча шарт бажарилиши лозим. Кўриб чиқилаётган тенгламада мавжуд бўлмаган, лекин тизимга кирган эндоген ва экзоген ўзгарувчиларни тизимда таъкидлаб чиқамиз. Бошқа тенгламаларда ўзгарувчилар коэффициентларидан матрицасини тузамиз. Агар ўзгарувчи тенгламанинг чап томонида жойлашган бўлса, бунда коэффициентни тескари белги билан олиш керак. Агар олинган матрицасини детерминанти нолга тенг бўлмаса ва даражаси бир кам тизимда эндоген ўзгарувчилар сонидан кам бўлмаса, бунда мазкур тенглама учун идентификациянинг етарли шарти бажарилган. Буни қуйидаги таркибли модел мисолида тушунтириб берамиз: y1= b12 y2 + b13 y3 + a11 x1 + a12 x2 y2= b21 y1 + a22 x2 + a23 x3 + a24 x4 (7) y3= b31 y1 + b32 y2 +a31 x1 + a32 x2 Ҳар бир тизимнинг тенгламасини керакли ва етарли идентификация шарти бажарилишига текшириб чиқамиз. Биринчи тенгламада учта эндоген ўзгарувчилар: y1 ,y2ваy3 (H=3) мавжуд. Унда экзоген ўзгарувчилар x3ва x4 (D=2) қатнашмаяпти. Керакли идентификация шарти бажарилган D+1=H. Керакли шартга текшириш учун x3ва x4 ўзгарувчилар коэффициентларидан иборат бўлган матрицасини тузамиз (3-жадвал). Жадвалнинг биринчи устунида экзоген ўзгарувчилар x3ва x4 коэффициентлари тизимининг 2 ва 3 тенгламалиридан олинган деб кўрсатилган. Иккинчи тенгламада мазкур ўзгарувчилар мавжуд бўлиб, уларнинг коэффициентлари a23 ва a24 ларга мос равишда тенг. Учинчи тенгламада юқоридаги ўзгарувчилар қатнашмайди, яъни уларнинг коэффициентлари нолга тенг. Матрицасининг иккинчи сатри нолдан иборат бўлгани учун, матрицанинг детерминанти хам нолга тенг. Демак, етарли шарти бажарилмаган ва биринчи тенгламани идентификацияланадиган деб ҳисобласа бўлмайди. 3-жадвал x3ва x4ўзгарувчилар коэффициентларидан тузилган матрица.
Иккинчи тенгламада иккита эндоген ўзгарувчилар: y1 и y2 (H=2) мавжуд. Бунда экзоген ўзгарувчи x1(D=1) қатнашмаяпти. Керакли идентификация шарти бажарилган D+1=H. Керакли шартга текшириш учун иккинчи тенгламада мавжуд бўлмаган y3ва x1 ўзгарувчилар коэффициентларидан иборат бўлган матрицасини тузамиз (4 -жадвал). 4 -жадвал y3 ва x1 ўзгарувчилар коэффициентларидан тузилган матрица.
Тенгламанинг чап томонида жойлашган учун учинчи тенгламада y3 ўзгарувчининг коэффициенти -1 тенг. Ҳақиқатда, учинчи тенгламани қуйидаги кўринишда ёзишимиз мумкин 0= b31 y1 + b32 y2 -1 y3 +a31 x1 + a32 x2 , бунда b33 = –1 тенглама аниқ шаклланмоқда. Умумий ҳолда ТМШ ўзгарувчиларнинг коэффициентлар матрицаси кўринишида ифодаланиши мумкин. Бу ҳолатда иккинчи тенглама қуйидаги вектор билан белгиланиши мумкин (b31 , b32 ,-1, a31 , a32, 0 , 0) , ҳамда бутун бир вақтли тенгламалар тизими (14) қуйидаги матрица билан ифодаланади: 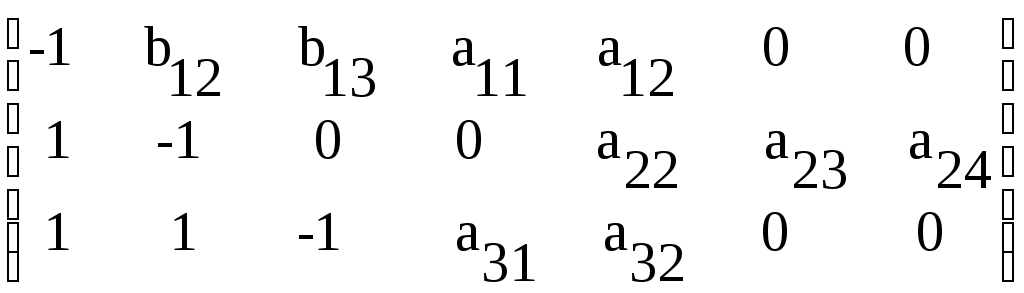 (15) (15)2-жадвалда келтирилган матрицанинг детерминанти нолга тенг эмас ва даражаси 2га тенг. Демак, етарли шарти бажарилган ва иккинчи тенглама идентификацияланадиган. Учинчи тенгламада учта эндоген ўзгарувчилар: y1 ,y2 и y3 (H=3) мавжуд. Бунда экзоген ўзгарувчилар x3ва x4 (D=2) қатнашмайди. Керакли идентификация шарти бажарилган D+1=H. Керакли шартга текшириш учун учинчи тенгламада мавжуд бўлмаган х3 ва x4 ўзгарувчилар коэффициентларидан иборат бўлган матрицасини тузамиз (5-жадвал). Жадвалга биноан матрицанинг детерминанти нолга тенг (биринчи сатри нолдан иборат). Демак, етарли шарти бажарилмаган ва учинчи тенгламани идентификацияланадиган деб ҳисобласа бўлмайди. 5-жадвал x3ва x4ўзгарувчилар коэффициентларидан тузилган матрица.
Эконометрик моделларда айрим ҳолларда ўзгарувчиларнинг балансли айнанликлар қўлланилади (масалан, y3=y1+y2+x1 кўринишдаги) Бунда ўзгарувчиларнинг коэффициентлари баҳолашни талаб қилмайди ва тенгламани идентификациялашга текшириш керак эмас, лекин бутун тизимни идентификацияга текширишда мазкур тенгламалар қатнашади. Айрим ҳолатларда моделда қатнашадиган озод ва қолдиқ ҳадлар (а01, а02, а03 ,…1, 2, 3,…) идентификациялаш муаммосига таъсир этмайди. Мустақил ишлаш учун назорат саволлари: Қайси ҳолларда бир вақтли эконометрик моделлар тузилади ва бунинг сабаби нимада? Бир вақтли тенгламалар тизимини ечишда қандай усуллардан фойдаланилади? Нима учун эконометрик моделлар тенгламалар тизими кўринишида ифодаланади? Тенгламлар тизимини идентификациялашда қандай муаммолар мавжуд? Тенгламалар тизимида эндоген ўзгарувчилар қандай танланади? Экзоген ўзгарувчилар нима ва улар эконометрик моделда қандай аҳамиятга эга? Тенгламалар тизимида лагли ўзгарувчилар қандай ҳисобга олинади? Бир вақтли тенгламалар тизимининг иқтисодий аҳамияти нимадан иборат? 8-мавзу. Амалий эконометрик моделлар 1. Иқтисодий ўсиш жараёнини ишлаб чиқариш функциялари ёрдамида тадқиқ этиш. 2. Ишлаб чиқариш функцияларининг характеристикалари. 3. Талаб ва таклифнинг эконометрик моделлари. 4. Макроиқтисодий эконометрик моделларнинг турлари ва уларни иқтисодий таҳлилда қўлланилиши. 1. Иқтисодий ўсиш жараёнини ишлаб чиқариш функциялари ёрдамида тадқиқ этиш. Ишлаб чиқариш жараёни кузатилаётганда кўриш мумкинки маҳсулот ишлаб чиқаришда хом-ашё, иш кучи, техника воситалари, электр энергияси, асосий фондлар ва бошқа ресурслар бевосита қатнашади ва маҳсулот ҳажмига таъсир этади. Ишлаб чиқарилган маҳсулот билан унга сарфланган ресурслар орасидаги боғланишни ишлаб чиқариш функцияси орқали кўрсатиш мумкин. Умумий ҳолда ишлаб чиқариш функцияси қуйидаги кўринишда ифодаланади. y = f ( x1, x2,..., xm), бу ерда y - ишлаб чиқарилган маҳсулот миқдори; хi – ресурслар сарфи. Иқтисодий жараёнларни моделлаштиришда асосий босқич – бу функция ва омиллар ўртасидаги алоқа шаклларини танлашдир. Бунга ё текширмай-нетмай мантиқий фикрларга асосланиб ёки амалий тажриба, экспериментлар асосида эришилади. Боғлиқликлар тўпламидан иқтисодий жараёни характерига мувофиқроқ келадиган ишлаб чиқариш функциясини танлашга моделланаётган объектнинг технологик, физик-биологик ва агротехник характеристикаларини ўрганиш асосида эришилади. Функция ва далиллар ўртасидаги боғлиқларни топиш аввал мазкур иқтисодий жараёнга мувофиқ келадиган эмпирик формулани топишдан иборат бўлади. Эмпирик формула алоқа характерининг яқинлаштирилган маъносини (қимматини) гина англатади, демак, танлаб олинган ишлаб чиқариш функцияси далиллар билан ўрганилаётган алоқа қонунини нисбатангина ифодалайди, бу эса назарий ишлаб чиқариш функциясига ўтиш лозимлигини кўрсатади. Эмпирик боғлиқликдан назарий функцияга ўтиш энг кичик квадратлар усули ёрдамида амалга оширилади. Унинг моҳияти шундай параметрларни топишдан иборатдирки, унда функциянинг ҳисобланган қийматлари билан унинг ҳақиқий қийматлари ўртасидаги фарқ квадратлари йиғиндиси энг минимал бўлиб, қуйидагича ифодаланади: Регрессия тенгламаси тўғри танланган бўлса, боғлиқликнинг назарий формаси ўрганилаётган алоқа қонуниятларини жуда аниқ акс эттиради. Ишлаб чиқариш функциялари математик тасвирлаш типига кўра чизиқли, даражали, параболик, кўрсаткичли ва ҳоказо бўлиши мумкин. Бу функцияларнинг баъзиларини кўриб чиқамиз. 1. Чизиқли функция: Бу функция бир жинсли бўлиб, омил-далилларнинг доимий лимитли самаралилиги билан характерлидир. Умуман иқтисодиёт учун чизиқсиз алоқа ҳам характерли бўлиб, маълум доиралардагина чизиқли ҳолатга, яъни (7) кўринишга келтирилади. 2. Даражали функция: бу ерда у - ишлаб чиқарилган маҳсулот; х - ишлаб чиқариш ресурслари сарфи; b - ишлаб чиқариш самарадорлигининг ўзгариш кўрсаткичи; а - эркин параметр. Мазкур функция қўшимча маҳсулотнинг қўшимча харажат бирлигига нисбатан доим ўсиб ёки камайиб боришини назарда тутади, бироқ у қўшимча маҳсулотнинг айни бир вақтда камайиши ва ўсиб боришига йўл қўймайди. Буни функциянинг биринчи тартибли ҳосиласида кўриш мумкин: 3) Кобба-Дуглас типдаги даражали функция энг кўп тарқалган ва универсал функция ҳисобланади. У қуйидагича кўринишда бўлади; бу ерда у - натижавий кўрсаткич; хi - эркин ўзгарувчи миқдор; Бу функция параметрлари бир вақтни ичида элстиклик коэффициентларига тенг. Эластиклик коэффициентларининг иқтисодий мазмуни шундан иборатки, улар мустақил ўзгарувчилар (х) бир фоизга ўзгарганда самарали (натижали) кўрсаткич (у) қандай ўзгаришини кўрсатади. Даражали функцияни харажатлар ўртача бўлганда ресурсларнинг унумдорлиги тадқиқотчини қизиқтирган вақтда қўлланиш назарда тутилади. Унинг формаси маҳсулот чиқаришда маълум ресурслар - меҳнат, ишлаб чиқариш фонди ва табиий ресурсларнинг иштирокини шарт қилиб қўювчи хусусиятларни акс эттиради. Бу мазкур функциянинг хилма-хил иқтисодий жараёнларни баён қилишда универсал қўлланилишини белгилайди. | |||||||||||||||||||||||||||||||||
