Вопросы к экзамену. Вопросы к экзамену (зачету)
 Скачать 2.73 Mb. Скачать 2.73 Mb.
|
|
Вопросы к экзамену (зачету).
Кинематика изучает движение тел, не рассматривая причины, которые обуславливают это движение, т. е. в ней дается только математическое описание механического движения тел безотносительно к причинам, вызывающих конкретный вид движения. Кинематика изучает механическое движение тела без рассмотрения причин вызывающих и изменяющих это движение. Тело отсчета – это тело по отношению к которому определяется положение других тел. Системой отсчета называется система координат, снабженная часами и жестко связанная с телом отсчета, по отношению к которому определяется положение других тел в различные моменты времени. Векторный способ описания движения основывается на задании радиус-вектора материальной точки (м.т.). Радиус-вектор – это вектор, соединяющий начало координат с положением материальной точки в данный момент времени. Приращение радиус-вектора называется вектором перемещения м.т. 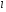 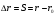 Перемещение – это вектор, соединяющий начальное и конечное положение материальной точки: Перемещение – это вектор, соединяющий начальное и конечное положение материальной точки: 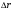 – пройденный путь. – пройденный путь.Вектор перемещения направлен вдоль хорды, стягивающей соответствующий участок траектории в случае криволинейного движения. Скорость. Скорость определяет быстроту, и направление движения материальной точки в данный момент времени. Скорость – ВФВ, характеризующая процесс изменения пространственного положения движущейся материальной точки равная перемещению, совершаемому точкой за единицу времени. Различают: 1) среднюю скорость; 2) мгновенную скорость; 3) среднюю путевую скорость. Средняя скорость. 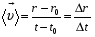 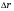 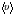 Средняя скорость - ВФВ, характеризующая быстроту движения на данном участке и равная отношению приращения радиус-вектора к рассматриваемому промежутку времени Dt: Средняя скорость - ВФВ, характеризующая быстроту движения на данном участке и равная отношению приращения радиус-вектора к рассматриваемому промежутку времени Dt: Вектор средней скорости всегда совпадает по направлению с вектором перемещения: Вектор средней скорости всегда совпадает по направлению с вектором перемещения:Размерность скорости [u] = 1 м/с 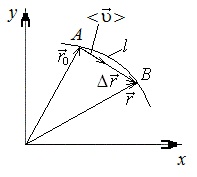 При неограниченном уменьшении промежутка времени Δt средняя скорость стремиться к предельному значению, которое называется мгновенной скоростью. 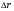 Мгновенная скорость u – ВФВ, характеризующая быстроту движения в данный момент времени и равная пределу отношения приращения радиус-вектора к бесконечно малому промежутку времени Δt, в течение которого это приращение произошло: Мгновенная скорость u – ВФВ, характеризующая быстроту движения в данный момент времени и равная пределу отношения приращения радиус-вектора к бесконечно малому промежутку времени Δt, в течение которого это приращение произошло: 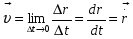 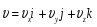 Вектор мгновенной скорости u разложим на три составляющие по координатным осям: Вектор мгновенной скорости u разложим на три составляющие по координатным осям:Проекции вектора скорости: 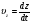 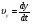 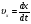 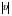 Модуль вектора скорости : 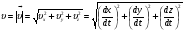 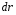 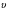 Направление вектора совпадает с направлением вектора элементарного перемещения точки , т. е. он направлен всегда по касательной к траектории. Направление вектора совпадает с направлением вектора элементарного перемещения точки , т. е. он направлен всегда по касательной к траектории.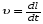 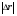 По мере уменьшения Δt путь Δl все больше будет приближаться к , поэтому модуль мгновенной скорости равен первой производной пути по времени: По мере уменьшения Δt путь Δl все больше будет приближаться к , поэтому модуль мгновенной скорости равен первой производной пути по времени: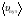 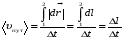 Средняя путевая скорость – СФВ, характеризующая среднюю быстроту изменения со временем пути и равная отношению пройденного пути Δl ко времени Δt, за которое этот путь был пройден: Средняя путевая скорость – СФВ, характеризующая среднюю быстроту изменения со временем пути и равная отношению пройденного пути Δl ко времени Δt, за которое этот путь был пройден: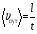 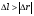 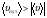 где l – путь, пройденный точкой за время t. где l – путь, пройденный точкой за время t.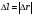 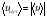 Для криволинейного движения: , т.к. Для криволинейного движения: , т.к. Для прямолинейного движения: ,т.к. . Ускорение. Быстроту изменения скорости с течением времени характеризует величина называемая ускорением. Ускорение – ВФВ, характеризующая процесс изменения скорости с течением времени и равная приращению скорости за единицу времени. Различают среднее и мгновенное ускорения. Среднее ускорение. 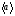 Среднее ускорение – ВФВ, характеризующая среднюю быстроту изменения скорости м.т. на всем пути и равная отношению приращения скорости к промежутку времени, в течение которого это произошло. Среднее ускорение – ВФВ, характеризующая среднюю быстроту изменения скорости м.т. на всем пути и равная отношению приращения скорости к промежутку времени, в течение которого это произошло.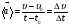 Ускорение имеет размерность [a] = 1 м/с2 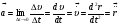 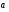 Мгновенное ускорение – ВФВ, характеризующая быстроту изменения скорости в данный момент времени и равная пределу отношения приращения скорости к бесконечно малому промежутку времени, в течение которого это приращение произошло: Мгновенное ускорение – ВФВ, характеризующая быстроту изменения скорости в данный момент времени и равная пределу отношения приращения скорости к бесконечно малому промежутку времени, в течение которого это приращение произошло: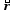 Таким образом, ускорение равно первой производной скорости по времени t, или второй производной радиус-вектора по времени t. Таким образом, ускорение равно первой производной скорости по времени t, или второй производной радиус-вектора по времени t.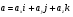 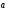 Вектор мгновенного ускорения разложим на три составляющие по координатным осям x, y, z: Вектор мгновенного ускорения разложим на три составляющие по координатным осям x, y, z: 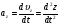 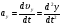 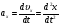 Проекция вектора ускорения на координатные оси: Проекция вектора ускорения на координатные оси: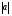 Модуль вектора ускорения : 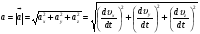 Вывод: определение скорости и ускорения сводится к чисто математической задаче вычисления первой и второй производных по времени радиуса вектора этой точки. Кинематика поступательного движения твердого тела МТ. 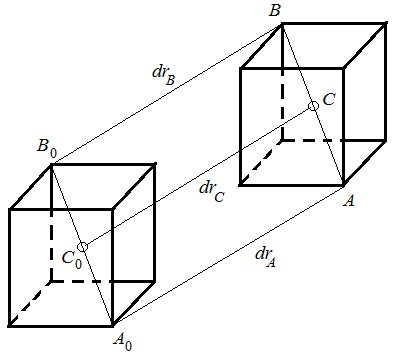  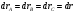 Поступательное движение является простейшим видом механического движения твердого тела, при котором прямая, соединяющая любые две точки этого тела, перемещаясь вместе с телом, остается параллельной своему первоначальному направлению. Поступательное движение является простейшим видом механического движения твердого тела, при котором прямая, соединяющая любые две точки этого тела, перемещаясь вместе с телом, остается параллельной своему первоначальному направлению.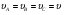 Где - радиусы-векторы точек А, В, С и произвольной точки М тела. Где - радиусы-векторы точек А, В, С и произвольной точки М тела.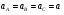 Следовательно, Следовательно, Вывод: из этих соотношений следует, что для кинематического описания поступательного движения твердого тела и МТ достаточно рассмотреть движение какой либо одной его точки.
Координатный способ. Координатный способ задает положение тела в пространстве с помощью координат тела. Переход от векторного описания движения к координатному осуществляется путем проектирования. Проекции радиус-вектора на координатные оси равны соответствующим координатам м.т.: rx = x; ry = y; rz = z. 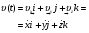 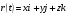 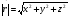 Обратный переход осуществляется с помощью теоремы Пифагора и направляющих косинусов: Обратный переход осуществляется с помощью теоремы Пифагора и направляющих косинусов: Направляющие косинусы: 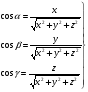 Числом степеней свободы называется число независимых координат, полностью определяющих положение точки (тела) в пространстве относительно выбранной системы отсчета. 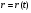 Законом движения материальной точки называется уравнение, выражающее зависимость ее радиуса-вектора от времени: Законом движения материальной точки называется уравнение, выражающее зависимость ее радиуса-вектора от времени: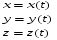 Спроектировав данное уравнение на оси координат, тогда зададим движение тела в прямоугольной (декартовой) системе координат: Спроектировав данное уравнение на оси координат, тогда зададим движение тела в прямоугольной (декартовой) системе координат:Данные уравнения кинематическими уравнениями движения материальной точки. Траекторией называется линия, которую описывает материальная точка при своем движении относительно выбранной системы отсчет. Естественный способ описания движения. В основу естественного способа описания движения положено уравнение траектории или пути, проходимого телом. 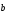 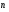 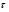 Естественный способ описания движения позволяет «привязать» описание движения к его траектории. В основе этого способа лежит естественная тройка векторов – вектор тангенциали , вектор нормали и вектор бинормали . Естественный способ описания движения позволяет «привязать» описание движения к его траектории. В основе этого способа лежит естественная тройка векторов – вектор тангенциали , вектор нормали и вектор бинормали .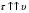 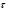 Вектор тангенциали - это вектор, касательный к траектории в данной точке. Вектор тангенциали - это вектор, касательный к траектории в данной точке.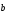 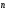 Вектор нормали - это вектор, направленный из данной точки к центру кривизны траектории. Вектор нормали - это вектор, направленный из данной точки к центру кривизны траектории.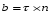 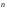 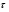 Вектор бинормали - это вектор, являющиеся векторным произведением тангенциали и вектора нормали . Вектор бинормали - это вектор, являющиеся векторным произведением тангенциали и вектора нормали . 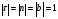 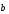 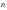 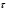 Векторы , , образуют правовинтовую систему. Она также является правой прямоугольной (декартовой) системой координат. Векторы , , образуют правовинтовую систему. Она также является правой прямоугольной (декартовой) системой координат.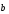 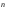 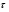 Если , то векторы станут ортами соответствующих осях. Если , то векторы станут ортами соответствующих осях.Скорость точки при естественном способе описания движения. 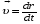 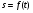 Движение точки задано естественным способом, т. е. известна траектория точки и закон ее движения по этой траектории . Вычислим скорость этой точки. Движение точки задано естественным способом, т. е. известна траектория точки и закон ее движения по этой траектории . Вычислим скорость этой точки.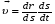 Воспользуемся определением скорости: Воспользуемся определением скорости: 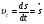 Правую часть до множим и разделим на ds. Получим: Правую часть до множим и разделим на ds. Получим: 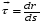 Где - модуль скорости движущейся точки. Где - модуль скорости движущейся точки.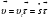 -единичный вектор тангенциали, направлен по касательной к траектории в -единичный вектор тангенциали, направлен по касательной к траектории вданной точке. Запишем: 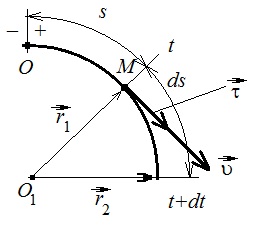 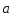 Ускорение точки при естественном способе описания движения. Ускорение точки при естественном способе описания движения.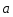 Траектория точки – плоская кривая, то ускорение точки лежит в данной плоскости. Траектория точки – плоская кривая, то ускорение точки лежит в данной плоскости. 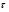 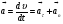 Вектор полного ускорения удобно разложить на две составляющие вдоль этих направлений: Вектор полного ускорения удобно разложить на две составляющие вдоль этих направлений: 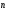 У плоскости имеются два направления – касательное к траектории (вектор тангенциали ) и главной нормали (вектор нормали ). У плоскости имеются два направления – касательное к траектории (вектор тангенциали ) и главной нормали (вектор нормали ).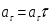 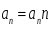 -называется тангенциальным ускорением; -называется тангенциальным ускорением;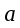 -называется нормальным ускорением (центростремительным ускорением) ; -называется нормальным ускорением (центростремительным ускорением) ;-называется вектором полного ускорения. 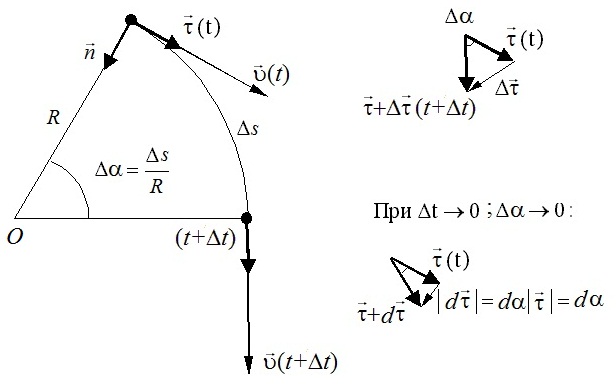 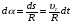 Ввиду малости этого участка траектории его можно считать совпадающим с соответствующим участком соприкасающейся окружности радиусом R с центром в точке О, которому соответствует центральный угол: Ввиду малости этого участка траектории его можно считать совпадающим с соответствующим участком соприкасающейся окружности радиусом R с центром в точке О, которому соответствует центральный угол: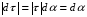 При перемещении по траектории на малое расстояние ds единичный вектор касательной поворачивается на угол dα. При перемещении по траектории на малое расстояние ds единичный вектор касательной поворачивается на угол dα. 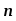 Ввиду малости dα следует: Ввиду малости dα следует: 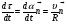 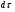 По направлением вектор совпадает с единичным вектором главной нормали . По направлением вектор совпадает с единичным вектором главной нормали .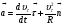 Таким образом, Таким образом, Для полного ускорения уравнение можно записать в виде: 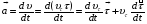 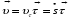 Для нахождения тангенциального и нормального ускорения воспользуемся формулой для скорости при естественном способе описании движения точки: Для нахождения тангенциального и нормального ускорения воспользуемся формулой для скорости при естественном способе описании движения точки: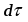 Следовательно, Следовательно,Где -приращение орта касательной к траектории, соответствующее элементарному пути проходимому точкой. 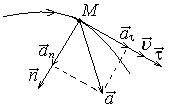 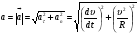 Модуль полного ускорения точки рассчитывается по формуле: Модуль полного ускорения точки рассчитывается по формуле:При криволинейном движении точки вектора его полного ускорения всегда отклонен от касательной траектории в сторону ее вогнутости.   Движение точки можно классифицировать в зависимости от тангенциальной и нормальной составляющих ускорения следующим образом: Движение точки можно классифицировать в зависимости от тангенциальной и нормальной составляющих ускорения следующим образом:
3.Кинематика вращательного движения МТ. Угловые характеристики движения. Связь между линейными и угловыми величинами. Кинематика вращательного движения твердого тела и МТ . А)Вращательным движением твердого тела называется движение, при котором все его точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения. Ось вращения может проходить как через вращающееся тело, так и находиться вне этого тела. Вращающееся тело имеет одну степень свободы вокруг неподвижной оси. Положение тела в пространстве определяется значением угла поворота вокруг оси вращения. 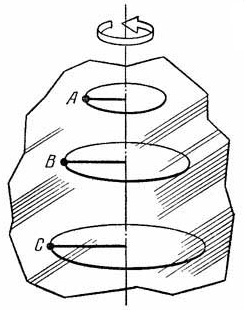 Б) Угловое перемещение. Рассмотрим вращение м.т. по окружности радиуса R. Пусть в начальный момент времени t0 м.т. находится в положении M и ее скорость равна u0. Спустя промежуток времени dt = t1 – t0 м.т. пройдет по окружности путь l и окажется в положении M1. Радиус-вектор точки, проведенный из центра O окружности, повернется на угол j. Угол j называется угловым путем (углом поворота). Размерность углового пути [j] = 1 рад. Из геометрии известно, что длина дуги, на которую опирается центральный угол MOM1, равна: l = jR Положение тела в пространстве полностью определяется значением угла поворота вокруг оси вращения из некоторого, условно выбранного начального положения этого тела. Для описания вращательного движения тела неудобно пользоваться понятиями кинематики, как: перемещение; пройденный путь; скорость и ускорение. 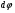 В случае вращательного движения мерой перемещения всего тела за малый промежуток времени dt служит вектор элементарного угла поворота тела . В случае вращательного движения мерой перемещения всего тела за малый промежуток времени dt служит вектор элементарного угла поворота тела . По модулю вектор элементарного угла поворота равен углу dφ поворота тела вокруг его оси вращения за время dt и направлен вдоль этой оси по правилу правого винта (правилу буравчика). |

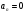
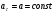 И -
И - 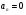
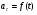 И - движение прямолинейное с переменным ускорением;
И - движение прямолинейное с переменным ускорением;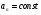
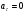 И - движение по окружности с постоянной скорости;
И - движение по окружности с постоянной скорости;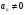
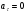 И - движение равномерное криволинейное;
И - движение равномерное криволинейное;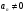
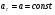 И - движение равнопеременное криволинейное;
И - движение равнопеременное криволинейное;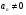
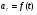 И - движение криволинейное с переменным ускорением.
И - движение криволинейное с переменным ускорением.