Вопросы к экзамену. Вопросы к экзамену (зачету)
 Скачать 2.73 Mb. Скачать 2.73 Mb.
|
|
33. Применение ПНТ к изопроцессам. Применение ПНТ к изопроцессам. Изотермический процесс (Т=const; m=const). 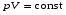 При изотермическом процессе изменяющиеся параметры p и V связаны законом Бойля – Мариотта: При изотермическом процессе изменяющиеся параметры p и V связаны законом Бойля – Мариотта: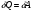 Так как Т=const, то и внутренняя энергия газа в этом процессе остается неизменной: dU=0 или ΔU=0. Следовательно ПНТ для изотермического процесса имеет вид: Так как Т=const, то и внутренняя энергия газа в этом процессе остается неизменной: dU=0 или ΔU=0. Следовательно ПНТ для изотермического процесса имеет вид:Т.е. подводимое количество теплоты идет на совершение газом внешней работы. 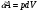 Найдем работу совершаемую газом в изотермическом процессе: Найдем работу совершаемую газом в изотермическом процессе: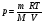 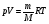 Давление р выразим из уравнения Менделеева–Клайперона: Давление р выразим из уравнения Менделеева–Клайперона:Или 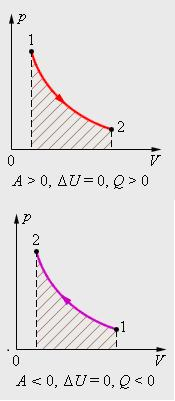 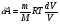 Подставим полученную формулу в выражение для работы, совершаемым ИГ при расширении от объема V1 до объема V2: Подставим полученную формулу в выражение для работы, совершаемым ИГ при расширении от объема V1 до объема V2: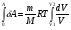 Проинтегрируем полученное уравнение: 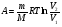 Получим: Графически работа при изотермическом процессе определяется площадью заштрихованной на рисунке фигуры. 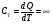 При изотермическом процессе изменение теплоты отлично от нуля, а изменение температуры равно нулю, то теплоемкость в данном процессе: При изотермическом процессе изменение теплоты отлично от нуля, а изменение температуры равно нулю, то теплоемкость в данном процессе:Изохорический процесс (V=const; m=const). 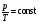 При изохорическом процессе изменяются параметры p и Т, которые связаны законом Шарля: При изохорическом процессе изменяются параметры p и Т, которые связаны законом Шарля: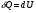 Из графика видно, что для изохорного процесса δА=0 и, следовательно, ПНТ для изохорического процесса имеет вид: Из графика видно, что для изохорного процесса δА=0 и, следовательно, ПНТ для изохорического процесса имеет вид: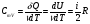 Молярная теплоемкость при изохорном процессе для ИГ определяется по формуле: Молярная теплоемкость при изохорном процессе для ИГ определяется по формуле: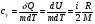 Удельная теплоемкость при изохорном процессе для ИГ определяется по формуле: Удельная теплоемкость при изохорном процессе для ИГ определяется по формуле: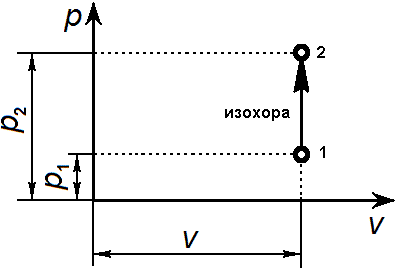 Изобарический процесс (р=const; m=const). 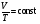 При изобарическом процессе изменяются параметры V и Т, которые связаны законом Гей-Люссака : При изобарическом процессе изменяются параметры V и Т, которые связаны законом Гей-Люссака : 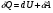 ПНТ для изобарного процесса имеет вид: ПНТ для изобарного процесса имеет вид: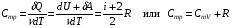 Молярная теплоемкость при изобарном процессе для ИГ определяется по формуле: Молярная теплоемкость при изобарном процессе для ИГ определяется по формуле: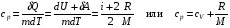 Удельная теплоемкость при изохорном процессе для ИГ определяется по формуле: Удельная теплоемкость при изохорном процессе для ИГ определяется по формуле: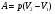 Работа совершаемая при изобарном процессе, определяется по формуле: Работа совершаемая при изобарном процессе, определяется по формуле:34. Адиабатный процесс. Уравнение Пуассона. Понятие о политропном поцессе. Адиабатический процесс (Q=0; m=const). 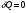 Адиабатический процесс – это процесс, происходящий без теплообмена с окружающей средой. Адиабатический процесс – это процесс, происходящий без теплообмена с окружающей средой. Для получения адиабатического процесса используют два способа: 1) поместить термодинамическую систему в теплонепроницаемую оболочку; 2) сделать процесс настолько быстрым, что теплообмен просто не успевает совершиться. Примерами первого способа является принцип действия обычного термоса, второго способа – работа дизельного двигателя (за счет быстрого сжатия горючей смеси она воспламеняется). Адиабата всегда круче изотермы. 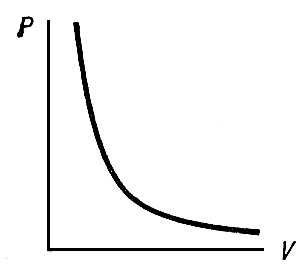 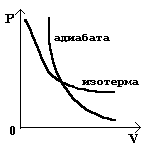 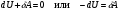 ПНТ для адиабатного процесса имеет вид: ПНТ для адиабатного процесса имеет вид: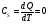 т.е. работа совершается за счет убыли внутренней энергии. Так как при этом ИГ меняет свою температуру без подведения количество теплоты, то теплоемкость ИГ при адиабатном процессе равна нулю: т.е. работа совершается за счет убыли внутренней энергии. Так как при этом ИГ меняет свою температуру без подведения количество теплоты, то теплоемкость ИГ при адиабатном процессе равна нулю:Адиабатный процесс называют изоэнтропийным (S=const, постоянная энтропия). При адиабатном процессе изменяются все три параметра состояния (давление, температура и объем). Используя ПНТ для адиабатного процесса и уравнение состояния ИГ, установим связь между этими параметрами состояния термодинамической системы (попарно). 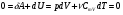 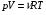 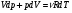 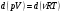 Найдем полный дифференциал от основного уравнения состояния идеального газа: Найдем полный дифференциал от основного уравнения состояния идеального газа: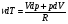 Отсюда: Отсюда: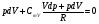 Подставим в ПНТ для адиабатного процесса, получим: Подставим в ПНТ для адиабатного процесса, получим: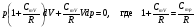 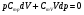 Получаем: 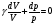 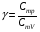 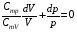 Разделим переменные выражение на pVCmV, получим Разделим переменные выражение на pVCmV, получим 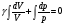 Проинтегрируем полученное выражение: 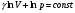 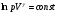 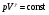 Уравнение адиабатного процесса: Уравнение адиабатного процесса: 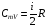 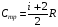 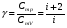 g - показатель адиабаты (коэффициент Пуассона). g - показатель адиабаты (коэффициент Пуассона). где , а , . При помощи основного уравнения состояния идеального газа можно получить уравнение адиабатического процесса и через другие основные параметры состояния. 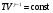  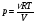 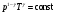 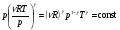 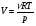 dQ = dU + dA = 0 Будем обозначать адиабатический процесс с индексом S: dUS = nCmVdT DUS = nCmVDT dAS = - dUS = - nCmVdT AS = - nCmVDT Получим более удобное для практических вычислений выражение для работы газа при адиабатическом процессе. 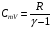 CmV= Cmp– R = gCmV– R CmV= Cmp– R = gCmV– R gCmV– CmV= R 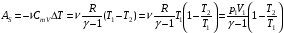 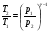 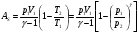 Из уравнения Пуассона: Из уравнения Пуассона: Работа при адиабатическом процессе: Политропический процесс. Политропический процесс – это процесс, который протекает при постоянной теплоемкости газа (С=const). Выше рассмотренные процессы являются частным случаем политропического процесса. 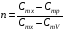 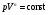 Уравнения политропического процесса: Уравнения политропического процесса:- показатель политропы где Cmx – молярная теплоемкость газа при данном изопроцессе. Можно показать, что уравнению политропического процесса удовлетворяют все изопроцессы в идеальных газах. 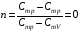 Например, для изобарического процесса имеем Сmх = Сmр Например, для изобарического процесса имеем Сmх = Сmр pV0 = p= const. 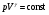 Очевидно, что при Сmх= 0, n = γ, тогда из уравнения политропического процесса получаем уравнение адиабаты: Очевидно, что при Сmх= 0, n = γ, тогда из уравнения политропического процесса получаем уравнение адиабаты: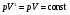 При Сmх = ¥, n = 1 – уравнение изотермы При Сmх = ¥, n = 1 – уравнение изотермыПри Сmх = СmV, n = ±¥ – уравнение изохорического процесса. Уравнение адиабатного процесса ( уравнение Пуассона). 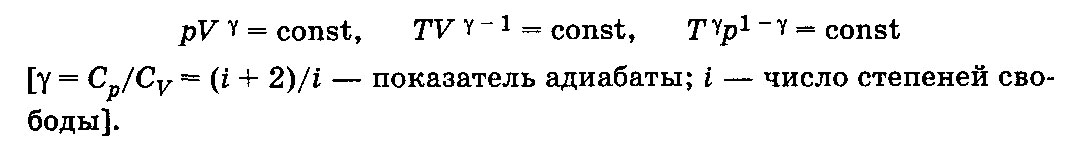 35. Второе начало термодинамики (ВНТ). Тепловые машины. Обратимые и необратимые термодинамические процессы. Круговые процессы. Обратимые процессы. В термодинамике большое значение имеет рассмотрение различных термодинамических процессов и циклов. Среди них: обратимые и необратимые; замкнутые и не замкнутые; круговые и некруговые циклы; а также специальные циклы и т.д. Обратимым процессом называется процесс при прохождении которого термодинамической системой в прямом, а затем в обратном направлении, система возвращается в исходное (первоначальное) состояние, при этом в окружающей среде не остается никаких следов (изменений). Примерами обратимых процессов могли бы быть все механические, электрические процессы, при которых не происходит потеря тепла. Признаками обратимых процессов являются следующие особенности: 1. Допускается обратный ход, путем простого изменения направления процесса. 2. Восстановление исходного состояния не требует подвода энергии из вне. 3. Процессы протекают без трения и теплопередачи. 4. Процесс не оставляет ни в одном из участвующих тел системы длительного изменения состояния. 5. Оба направления процессов (прямое и обратное) являются равноправными и равновероятными. Рассмотрение обратимых процессовважно по двум причинам: 1) многие процессы в природе и технике практически обратимы; 2) Обратимые процессы являются наиболее экономичными; имеют максимальный КПД, что позволяет указать пути повышения КПД реальных тепловых двигателей. Необратимые процессы. Тепловые процессы которые могут протекать только в одном направлении называются необратимыми процессами. Как показывает опыт, многие тепловые процессы являются необратимыми. Например, при тепловом контакте двух тел с разными температурами тепловой поток всегда направлен от более теплого тела к более холодному. Никогда не наблюдается самопроизвольный процесс передачи тепла от тела с низкой температурой к телу с более высокой температурой. Следовательно, процесс теплообмена при конечной разности температур является необратимым. Необратимыми являются процессыпревращения механической работы во внутреннюю энергию тела из-за наличия трения, процессы диффузии в газах и жидкостях, процессы перемешивания газа при наличии начальной разности давлений и т. д. Все реальные процессы необратимы, но они могут сколь угодно близко приближаться к обратимым процессам. Признаками необратимых процессов являются следующие особенности: 1. Необратимые процессы идут сами по себе лишь в одном направлении. 2. Энергия этих процессов тратиться без восстановления, упускается возможность совершить полезную работу. 3. Состояние термодинамической системы изменяется на длительное время. Таким образом, с учетом этих признаков можно утверждать, что все реальные процессы являются необратимыми. Обратимые процессы являются идеализацией реальных процессов. Работа в обратимых и необратимых процессах. Рассмотрим расширение газа в пустоту. В начальный момент времени весь газ находился в нижней части цилиндра под перегородкой, а между поршнем и перегородкой газа нет. В перегородке образуется отверстие и газ занимает все пространство под поршнем и самопроизвольно установиться новое давление одинаковое на разных участках. Этот процесс имеет только одно направление, т.е. он необратимый. Газ самопроизвольно перешел из одного состояния в другое, и он никогда не вернется в исходное состояние без внешних воздействий. В данном случае интенсивность теплового движения молекул газа не изменилась, так как температура оставалась постоянной. 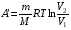 Чтобы вернуть газ в начальное состояние нужно произвести изотермическое сжатие. Чтобы вернуть газ в начальное состояние нужно произвести изотермическое сжатие.При этом внешние силы совершают работу, равную: 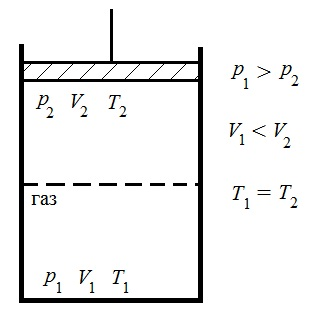 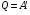 Во время изотермического сжатия от газа отводиться тепло окружающим телам: Во время изотермического сжатия от газа отводиться тепло окружающим телам:При этом какое-то внешнее тело оказывается нагретым. В цилиндре, как в некоторой термодинамической системе, произошло изменение, сопровождающееся уменьшением порядка в системе. При расширении в пустоту, газ не совершал работу против внешних сил. При этом расширении не было равновесия между различными частями газа и между газом и внешними телами. Этот процесс не был равновесным. 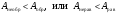 Необратимые процессы являются неравновесными процессами, так как работа, совершаемая газом над внешними телами всегда меньше, чем работа, совершаемая системой при том же самом изменении параметров в обратимом процессе. Необратимые процессы являются неравновесными процессами, так как работа, совершаемая газом над внешними телами всегда меньше, чем работа, совершаемая системой при том же самом изменении параметров в обратимом процессе.Суть второго начала термодинамики: самопроизвольные процессы протекают в направлении увеличения беспорядочный движения частиц за счет упорядоченных. Строгие формулировки ВНТ дадим позднее. Круговые процессы. Круговым процессом (циклом) называется такая термодинамическая последовательность превращений, в результате которых система, выйдя из какого-либо исходного состояния вновь в него возвращается. На диаграмме цикл изображается замкнутой кривой. Цикл, который совершает идеальный газ, можно разбить на процессы расширения (1—a—2) и сжатия (2—b—1) газа. Работа расширения (равна площади фигуры 1a2V2V11) положительна (dV>0), работа сжатия (равна площади фигуры 2b1V1V22) отрицательна (dV<0). Следовательно, работа, которую совершает газ за цикл, равен площади, охватываемой замкнутой кривой. Если за цикл совершается положительная работа A=∫pdV>0 (цикл идет по часовой стрелке), то он называется прямым. Если за цикл осуществляется отрицательная работа A=∫pdV<0 (цикл идет против часовой стрелки), то он называется обратным. 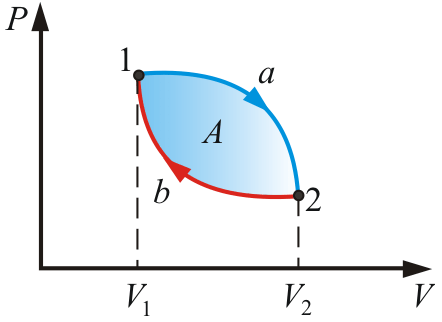 Прямой цикл применяется в тепловых двигателях — периодически действующих двигателях, которые совершают работу за счет полученной извне теплоты. Обратный цикл применяется в холодильных машинах — периодически действующих установках, в которых за счет работы внешних сил теплота переходит к телу с более высокой температурой. 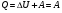 В результате кругового процесса система возвращается в исходное состояние и, значит, полное изменение внутренней энергии газа есть нуль. Поэтому первое начало термодинамики для кругового процесса: В результате кругового процесса система возвращается в исходное состояние и, значит, полное изменение внутренней энергии газа есть нуль. Поэтому первое начало термодинамики для кругового процесса: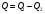 т. е. работа, которая совершается за цикл, равна количеству теплоты, полученной извне. Однако в результате кругового процесса система может теплоту как получать, так и отдавать, поэтому т. е. работа, которая совершается за цикл, равна количеству теплоты, полученной извне. Однако в результате кругового процесса система может теплоту как получать, так и отдавать, поэтому 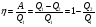 где Q1 — количество теплоты, которая получила система, Q2 — количество теплоты, которое отдала система. Поэтому термический коэффициент полезного действия для кругового процесса: где Q1 — количество теплоты, которая получила система, Q2 — количество теплоты, которое отдала система. Поэтому термический коэффициент полезного действия для кругового процесса:Макро- и микросостояние. Термодинамическая вероятность (статистический вес) данного макросостояния. Первое начало термодинамики указывает на возможность теплового процесса. Второе начало термодинамики указывает на направление теплового процесса. |
