Вопросы к экзамену. Вопросы к экзамену (зачету)
 Скачать 2.73 Mb. Скачать 2.73 Mb.
|
|
Эмпирическое уравнение диффузии, закон Фика : где D – коэффициент диффузии. Знак минус в уравнении Фика обусловлен тем, что поток направлен в сторону убывания концентрации. Умножим обе части уравнения Фика на массу молекулы i-го газа mi, получим. 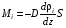 Закон Фика. Закон Фика.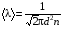 Выведем уравнение диффузии, исходя из молекулярно-кинетических представлений. Будем считать, что молекулы обоих газов мало отличаются по массе (m1≈m2≈m) и имеют практически одинаковые эффективные диаметры (d1≈d2≈d). В этом случае молекулам обоих газов можно приписать одинаковую среднюю скорость теплового движения, а среднюю длину свободного пробега вычислить по формуле: Выведем уравнение диффузии, исходя из молекулярно-кинетических представлений. Будем считать, что молекулы обоих газов мало отличаются по массе (m1≈m2≈m) и имеют практически одинаковые эффективные диаметры (d1≈d2≈d). В этом случае молекулам обоих газов можно приписать одинаковую среднюю скорость теплового движения, а среднюю длину свободного пробега вычислить по формуле:где n=n1+n2 – общая концентрация газов 1 и 2. 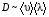 Процесс диффузии в газах будет протекать тем интенсивнее, чем быстрее движутся молекулы, а так же чем реже сталкиваются они друг с другом, т.е. чем больше у них длина свободного пробега λ. Следовательно можно предполагать, что коэффициент диффузии D пропорционален произведению средней скорости и средней длине свободного пробега. Процесс диффузии в газах будет протекать тем интенсивнее, чем быстрее движутся молекулы, а так же чем реже сталкиваются они друг с другом, т.е. чем больше у них длина свободного пробега λ. Следовательно можно предполагать, что коэффициент диффузии D пропорционален произведению средней скорости и средней длине свободного пробега.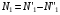 Пусть изменение концентрации первого газа вдоль оси z описывается функцией n1(z). Обозначим число молекул первого газа, пролетающих в единицу времени сквозь воображаемую поверхность S в направлении оси z, через N’1; то же число для противоположного направления – через N”1. Разность этих чисел даст поток N1 молекул первого газа через поверхность S: Пусть изменение концентрации первого газа вдоль оси z описывается функцией n1(z). Обозначим число молекул первого газа, пролетающих в единицу времени сквозь воображаемую поверхность S в направлении оси z, через N’1; то же число для противоположного направления – через N”1. Разность этих чисел даст поток N1 молекул первого газа через поверхность S: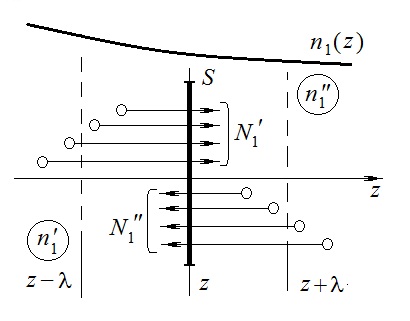 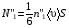 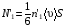 Количество молекул первого газа, пролетающих в единицу времени через поверхность S в каждом направлений (слева направо и справа на лево), будем рассчитывать по формулам: Количество молекул первого газа, пролетающих в единицу времени через поверхность S в каждом направлений (слева направо и справа на лево), будем рассчитывать по формулам:где n’1 – «эффективная» концентрация молекул первого газа слева от S, а n”1 – «эффективная» концентрация молекул первого газа справа от S. 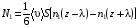 Через поверхность S пролетают молекулы, претерпевшие последнее соударение на различных расстояниях от этой поверхности. Однако в среднем последнее соударение происходит на расстоянии от S, равном средней длине свободного пробега λ. Поэтому в качестве n’1 взять значение n1(z–λ), а в качестве n”1 – значение n1(z+λ). Тогда для N1 получаем: Через поверхность S пролетают молекулы, претерпевшие последнее соударение на различных расстояниях от этой поверхности. Однако в среднем последнее соударение происходит на расстоянии от S, равном средней длине свободного пробега λ. Поэтому в качестве n’1 взять значение n1(z–λ), а в качестве n”1 – значение n1(z+λ). Тогда для N1 получаем: 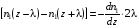 Разность значений функции n1(z) можно представить в виде: Разность значений функции n1(z) можно представить в виде: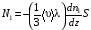 Подставим это выражение в закон Фика, получим: Подставим это выражение в закон Фика, получим: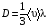 Выражение для коэффициента диффузии имеет вид : 30. Явление вязкости теплопроводности. Вязкость (внутреннее трение). Закон Ньютона. Коэффициент вязкости. Вязкость (внутреннее трение) связано с возникновением сил трения между слоями газа (жидкости), перемешивающимися друг с другом с различными по модулю скоростями. Со стороны слоя движущегося быстрее, на более медленно движущийся слой действует ускоряющая сила и наоборот, медленно перемещающийся слой тормозит более быстро движущиеся слои газа (жидкости). Силы трения которые при этом возникают, направлены по касательной к поверхности соприкосновения слоев. С молекулярно-кинетической точки зрения причиной вязкости является упорядоченное движение слоев с различными скоростями u и хаотичного движения молекул υ. 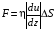 Согласно закону Ньютона сила трения между двумя слоями газа или жидкости равна. Согласно закону Ньютона сила трения между двумя слоями газа или жидкости равна.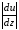 Эмпирическое уравнение вязкости, закон Ньютона: Эмпирическое уравнение вязкости, закон Ньютона:где η – коэффициент вязкости; - величина показывающая, как быстро изменяется 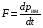 скорость течения жидкости или газа в направлении z, перпендикулярном к направлению движения слоев (градиент скорости u), S – площадь лежащей на границе между слоями поверхности, по которой действует сила F. скорость течения жидкости или газа в направлении z, перпендикулярном к направлению движения слоев (градиент скорости u), S – площадь лежащей на границе между слоями поверхности, по которой действует сила F. 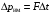 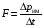 Согласно 2-му закону Ньютона: Согласно 2-му закону Ньютона: 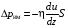 или, , тогда или, , тогда Уравнение Ньютона для внутреннего трения можно представить в виде: где Δрим – импульс, передаваемый от слоя к слою за секунду (Δt=1 с), т.е. поток импульса через поверхность S. Знак «минус» в формуле обусловлен тем, что импульс «течет» в направлении убывания скорости u. Поэтому знаки импульса и градиента скорости u противоположны. 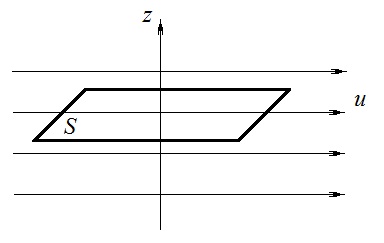 В формуле Ньютона минус писать нельзя, потому что она определяет одинаковый модуль двух противоположно направленных сил, с которыми слои действуют друг на друга. Кроме того нужно брать модуль градиента скорости, так как производная может иметь любой знак, а модуль силы – положительная величина. 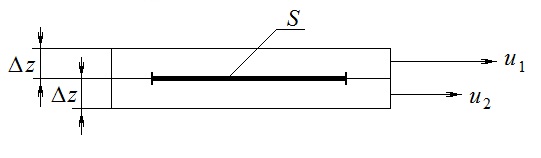 Рассмотрим происхождение силы внутреннего трения. Рассмотрим два соприкасающихся слоя газа толщиной Δz. Слои движутся с различными скоростями u1 и u2. Каждая молекула газа участвует в двух движениях: хаотическом тепловом, средняя скорость которого равна <υ>, и упорядоченном движении со скоростью потока u. Скорость потока намного меньше, чем скорость теплового движения. В неподвижном газе средний импульс молекулы равен нулю. Молекула в потоке газа обладает средним импульсом mu. При рассмотрении внутреннего трения нас будет интересовать этот импульс. Пусть в некоторый момент времени слои обладают импульсами рим1 и рим2. При отсутствии внешнего воздействия на слои, их импульсы не могут оставаться неизменными, так как вследствие теплового движения происходит непрерывный переход молекул из одного слоя в другой. Попав в другой слой, молекула претерпевает столкновения с молекулами этого слоя, в результате чего она отдает избыток своего импульса другим молекулам ( если она прилетела из слоя, движущегося быстрее), либо увеличивает свой импульс за счет других молекул (если она прилетела из слоя, движущегося медленнее). В итоге импульс слоя, движущегося быстрее, убывает, а слоя, движущегося медленнее, возрастает. Следовательно, слои ведут себя так, как если бы к слою, скорость которого больше, была приложена сила, тормозящая его движение, а к слою, скорость которого меньшая, - такая же по модулю сила, ускоряющая его движение. Таков механизм возникновения сил внутреннего трения. 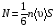 Через поверхность S, лежащую на границе раздела слоев, переходит в единицу времени из одного слоя в другой количество молекул, определяемое выражением: Через поверхность S, лежащую на границе раздела слоев, переходит в единицу времени из одного слоя в другой количество молекул, определяемое выражением: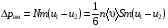 на среднюю скорость молекул в направлении, перпендикулярном к слоям, движение слоев со скоростью u не оказывает влияния). В результате возникает в направлении от более быстрого слоя к более медленному поток импульса через поверхность S, равный: на среднюю скорость молекул в направлении, перпендикулярном к слоям, движение слоев со скоростью u не оказывает влияния). В результате возникает в направлении от более быстрого слоя к более медленному поток импульса через поверхность S, равный:В реальном потоке газа скорость при переходе через воображаемую границу двух слоев изменяется не скачком, а непрерывно по закону u=u(z). Будем считать, что каждая молекула, пролетающая через поверхность S, несет с собой импульс mu, определяемый скоростью u в том месте, где произошло столкновение молекулы. Это столкновение происходит на различных расстояниях от S. В среднем последнее столкновение происходит на расстоянии, равном длине свободного пробега λ. Поэтому молекулам, летящим в направлении оси z, припишем значение скорости u1=u(z–λ), а молекулам, летящим в противоположном направлении, – значение скорости u2=u(z+λ). Подстановка этих значений в формулу для потока импульса через поверхность S в направлении оси z дает выражение: 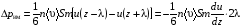 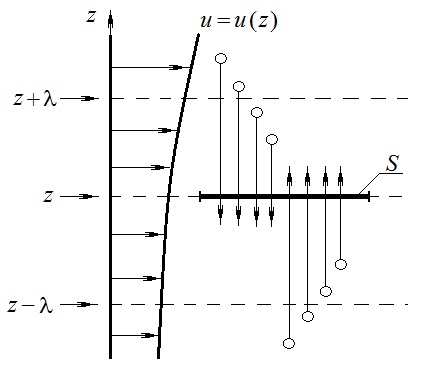 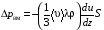 Произведение nm равно плотности газа ρ. Поэтому полученное уравнение можно записать в виде: Произведение nm равно плотности газа ρ. Поэтому полученное уравнение можно записать в виде: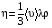 Сравнение полученного уравнения с эмпирической формулой Ньютона дает для вязкости выражение: Сравнение полученного уравнения с эмпирической формулой Ньютона дает для вязкости выражение:Размерность вязкости [η] = 1 (кг/(м∙с)) = 1 (Па∙с). Теплопроводность. Закон Фурье. Коэффициент теплопроводности. Теплопроводность возникает при наличии разности температур, вызванной какими-либо внешними причинами. При этом молекулы газа в разных местах имеют разные средние кинетические энергии (скорости хаотического теплового движения молекул), что приводит к направленному переносу молекулами газа внутренней энергии. 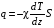 Опытным путем установлено, что в случае, если в какой-либо среде вдоль некоторого направления z температура не остается постоянной, то вдоль этого направления устанавливается поток тепла, величина которого определяется формулой. Опытным путем установлено, что в случае, если в какой-либо среде вдоль некоторого направления z температура не остается постоянной, то вдоль этого направления устанавливается поток тепла, величина которого определяется формулой.Закон Фурье: 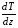 где q – количество теплоты, протекающее за единицу времени через площадку S, расположенную перпендикулярно к оси z, c – коэффициент теплопроводности; где q – количество теплоты, протекающее за единицу времени через площадку S, расположенную перпендикулярно к оси z, c – коэффициент теплопроводности;Градиент температуры: Знак «минус» в законе Фурье отражает то обстоятельство, что направление, в котором возрастает температура, и направление, в котором течет тепло, противоположны, т.е. что тепло течет в направлении убывания температуры. Поток тепла в уравнении Фурье – величина алгебраическая: если тепло течет в положительном направлении оси z, q положительно, если же тепло течет в отрицательном направлении оси z, то q отрицательно. 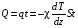 Чтобы вычислить количество теплоты Q, протекающее через площадку S за время t, нужно q умножить на t: Чтобы вычислить количество теплоты Q, протекающее через площадку S за время t, нужно q умножить на t:Вычислим поток тепла в газе, основываясь на молекулярно-кинетических представлениях. Если температура газа в разных местах различна, то и средняя энергия молекул также будет различной. Перемещаясь вследствие теплового движения из одних мест в другие, молекулы переносят запасенную ими энергию, что обуславливает процесс теплопроводности. Кроме факторов, определяющих скорость диффузии, т.е. средней скорости молекул , <υ> и длины свободного пробега λ, количество переносимой молекулами энергии должно зависеть от способности молекул запасать энергию, т.е. От теплоемкости газа. Поскольку поток молекул определяется их числом в единице объема, то и теплоемкость должна относиться к единице объема. 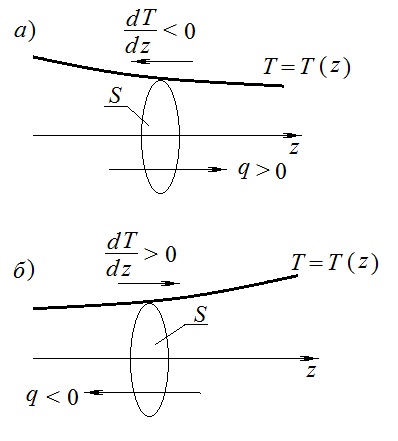 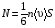 Пусть в газе поддерживается градиент температуры вдоль направления z. Представим мысленно поверхность S, перпендикулярно к этому направлению. Количество молекул, пролетающих в единицу времени через поверхность S в каждом направлений (слева направо и справа на лево), будем считать равным: Пусть в газе поддерживается градиент температуры вдоль направления z. Представим мысленно поверхность S, перпендикулярно к этому направлению. Количество молекул, пролетающих в единицу времени через поверхность S в каждом направлений (слева направо и справа на лево), будем считать равным: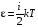 Вычислим тепловой поток. Вычислим тепловой поток.Каждая молекула имеет энергию , соответствующую температуре в том месте, где произошло ее столкновение с другой молекулой. В среднем это столкновение происходит на расстоянии от S, равном длине свободного пробега λ. Поэтому молекулам, летящим слева на право, надо приписывать среднюю энергию <ε1>, соответствующую температуре Т1=Т(z–λ), т.е. температуре в плоскости z–λ, молекулам же, летящим справа налево – среднюю энергию <ε2>, соответствующей температуре Т2=Т(z+λ). Величины n и <υ> зависят от температуры. Число частиц, летящих через площадку S во встречных направлениях, не могут быть различными. Если бы они оказались неодинаковыми, то кроме потока тепла через площадку S наблюдался бы поток вещества (диффузия) – происходило бы перемещение газа из одной части пространства в другую. В самом начале сделали предположение, что движение газа, как целого, отсутствует. 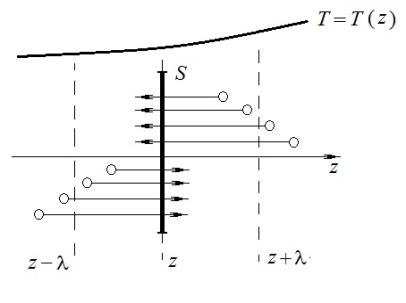 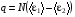 Таким образом, для теплового потока q через поверхность S получается выражение: Таким образом, для теплового потока q через поверхность S получается выражение:где N определяется формулой . 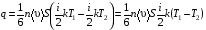 Подстановка значений N, <ε1> и <ε2> приводит к формуле: Подстановка значений N, <ε1> и <ε2> приводит к формуле: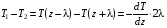 Вследствие малости λ разность Т1–Т2 можно представить в виде: Вследствие малости λ разность Т1–Т2 можно представить в виде: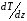 где - производная Т по z в том месте, где расположена поверхность S. Подстановка выражения для разности температур приводит к формуле Фурье: 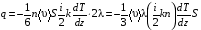 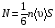 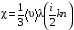 Полученная формула совпадает с эмпирическим уравнением Фурье, если положить теплоемкость равной: Полученная формула совпадает с эмпирическим уравнением Фурье, если положить теплоемкость равной: 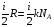 Величина молярная теплоемкость газа при постоянном объеме. 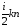 Следовательно выражение представляет собой теплоемкость при постоянном. 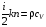 объеме количества газа, содержащего n молекул, т.е. теплоемкость единицы объема газа. Эту теплоемкость можно получить, умножив удельную теплоемкость газа сV при постоянном объеме на плотность газа ρ. Следовательно объеме количества газа, содержащего n молекул, т.е. теплоемкость единицы объема газа. Эту теплоемкость можно получить, умножив удельную теплоемкость газа сV при постоянном объеме на плотность газа ρ. Следовательно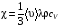 Учитывая это значение, получим для теплопроводности газа следующее выражение: Учитывая это значение, получим для теплопроводности газа следующее выражение:31. Первое начало термодинамики (ПНТ). Введение в термодинамику. Термодинамическая система - это совокупность тел, подверженных общему тепловому воздействию. Термодинамические параметры состояния системы – это физические величины, характеризующие состояние термодинамической системы. К ним можно отнести, например, массу газа, температуру, давление газа, его объем, теплоемкость и т.д. К основным термодинамическим параметрам состояния системы относят давление, объем и температуру. Термодинамический процесс – это процесс изменения термодинамических параметров системы. Состояние термодинамического равновесия – это состояние, при котором параметры состояния остаются неизменными в любых точках системы. Равновесный процесс - это процесс, при котором газ из начального в конечное состояние переходит путем прохождения таких равновесных состояний. В зависимости от возможных способов изоляции от внешней среды различают следующие виды термодинамических систем: открытая; закрытая; изолированная; замкнутая; адиабатическая. Открытой термодинамической системой называется система, которая может обмениваться веществом с внешней средой. Закрытая термодинамическая система не можем обмениваться веществом с внешней средой. Изолированная термодинамическая система не может обмениваться с внешней средой ни энергией, ни веществом. Замкнутая термодинамическая система – это система, которая изолирована в механическом отношении от окружающей среды, т.е. она не способна к обмену энергией с внешней средой путем совершения работы. Адиабатной термодинамической системой называется система, если она не может обмениваться с внешней средой энергией путем теплообмена. Внутренняя энергия. Первое начало термодинамики (ПНТ)  Внутренняя энергия является однозначной функцией состояния термодинамической системы. Значение внутренней энергии системы в каком-либо произвольном состоянии не зависит от того, каким образом система пришла в это состояние. Т.е. изменение внутренней энергии ΔU1-2 при переходе системы из состояния 1 в состояние 2 не зависит от вида процесса и равно: Внутренняя энергия является однозначной функцией состояния термодинамической системы. Значение внутренней энергии системы в каком-либо произвольном состоянии не зависит от того, каким образом система пришла в это состояние. Т.е. изменение внутренней энергии ΔU1-2 при переходе системы из состояния 1 в состояние 2 не зависит от вида процесса и равно: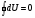 Если в результате каких-либо процессов система возвращается в исходное состояние, то полное изменение внутренней энергии равно нулю. Если в результате каких-либо процессов система возвращается в исходное состояние, то полное изменение внутренней энергии равно нулю.Обмен энергией между закрытой термодинамической системой и внешней средой может быть осуществлен двумя способами: совершением работы над термодинамической системой и путем теплообмена. Энергия, передаваемая при этом рассматриваемой термодинамической системе внешними телами, называется работой, совершаемой над системой. Энергия, передаваемая системе внешними телами путем теплообмена, называется количеством теплоты, получаемой системой от внешней среды. |
