вышмат. 1. Числоваяпоследовательности и ее предел
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
    1.Числоваяпоследовательности и ее предел. 1.Числоваяпоследовательности и ее предел.Функция f(x)называется функцией целочисленного аргумента, если множество значений x,для которых она определена, является множеством всех натуральных чисел1, 2, 3,… Примером функции целочисленного аргумента может служить сумма nпервых чисел натурального ряда. В данном случае Числовой последовательностьюназывается бесконечное множество чисел (1) следующих одно за другим в определенном порядке и построенных по определенному закону, с помощью которого задается как функция целочисленного аргумента, т.е. . ЧислоАназывается пределом последовательности(1), если для любого существует число, такое, что привыполняется неравенство.Если число А есть предел последовательности (1), то пишут Числовая последовательность не может иметь более одного предела. Последовательность, имеющая предел, называется сходящейся. Для сходящихся последовательностей имеют место теоремы: если . Пример 1. Найти общий член последовательности 1, 4, 9, 16, 25, … Р е ш е н и е : нетрудно видеть, что Следовательно Пример 2. Найти общий член последовательности Р е ш е н и е : не трудно видеть, что , 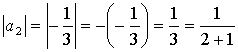 , и т.д. Следовательно: 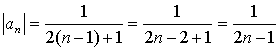 Пример 3. Доказать, что последовательность с общим членом имеет предел, равный нулю. Р е ш е н и е : запишем ряд членов последовательности и положим . Для всех членов данной последовательности, начиная с четвертого, выполняется равенство Действительно В данном случае N(см. определение предела последовательности) можно принять равным трем (или любому числу, больше трех), так как, если порядковый номер члена последовательности n больше трех, то выполняется неравенство . Положим теперь . Ясно, что для всех членов последовательности начиная с седьмого, . Теперь за N можно принять шесть (или любое число, большее шести). Если , то и т.д. В данном случае можно найти общее выражение для числа N в зависимости от . Общий член данной последовательности . Задавшись произвольным положительным числом , мы должны в соответствии с определением предела, потребовать, чтобы при n>N выполнялось неравенство , если . Решая неравенство относительно n, получаем . Итак, за N можно принять число (или любое большее число). Таким образом, мы показали, что для любого существует такое , чтопри , выполняется неравенство , а это и доказывает, что пределом последовательности является нуль. Отметим, что в этой задаче члены последовательности приближались к своему пределу, оставаясь больше этого предела, как говорят, справа. 2.Способы задания функции. 1. Аналитический способ Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее употребительным является способ задания функции с помощью формулы у = f (х), где f (х) - некоторое выражение с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически. Для аналитически заданной функции иногда не указывают явно область определения функции. В таком случае подразумевают, что область определения функции у = f (х) совпадает с областью определения выражения f (х), т. е. с множеством тех значений х, при которых выражение f (х) имеет смысл. 2. Табличный способ На практике часто используется табличный способ задания функции. При этом способе приводится таблица, указывающая значения функции для имеющихся в таблице значений аргумента. Примерами табличного задания функции являются таблица квадратов, таблица кубов, таблица квадратных корней. Во многих случаях табличное задание функции оказывается удобным. Оно позволяет найти значения функции для значений аргумента, имеющихся в таблице, без всяких вычислений. На практике часто зависимость одной величины от другой находят опытным путем. В этом случае одной величине придают определенные значения, а потом из опыта для каждого из таких значений находят значение (обычно приближенное) второй величины. Таким образом опыт позволяет составить некоторую таблицу значений функции. Существуют методы, позволяющие по такой таблице подбирать формулы, задающие функции (с определенной точностью). 3. Графический способ Часто функция может быть задана с помощью графика.. |
