Маркетинговые показатели. 1 Что такое система показателей
 Скачать 19.01 Mb. Скачать 19.01 Mb.
|
|
Средняя цена единицы = Выручка ($) товара ($) Количество проданных единиц (#) или = [Цена единицы SKU I ($) х Процент продаж SKU 1 (%)] + [Цена единицы SKI 2 ($) х Процент продаж SKU 2 (%)] + и т. д. Средняя цена за единицу товара зависит как от штучных цен, так и от единичных продаж отдельных SCU. Средняя цена за единицу товара может увеличиваться вследствие роста штучных цен или доли штучных продаж более дорогостоящих SCU, или в результате воздействия обоих этих факторов. Показатель средней цены, который нечувствителен к изменениям долей SCU, является ценой статистической единицы. Цена статистической единицы Компания Procter & Gamble и другие фирмы сталкиваются с проблемой мониторинга цен при широком разнообразии форматов товара, типов упаковки и технологий производства продукции. У некоторых брендов имеется до 25-30 разных SCU, и каждая из них имеет свою цену. Как в таких обстоятельствах маркетологи определяют общий уровень цен бренда с тем, чтобы сравнить его с предложениями конкурентов, или отследить, повышаются ли цены или падают? Одним из решений является статистическая единица, которая называется также статистическим ящиком, или - в показателях объема или массы - статистическим литром, статистической тонной. Статистическая единица 288 унций жидкого моющего средства, например, может включать в себя: четыре 4-унциевых флакона = 16 унций; двенадцать 12-унциевых флаконов = 144 унции; два 32-унциевых флакона = 64 унции; один 64-унциевый флакон = 64 унции. Следует иметь в виду, что содержание данного статистического ящика было предусмотрительно выбрано так, чтобы он содержал такое же количество унций, как и стандартный ящик вместимостью двадцать четыре 12-унциевых флакона. Таким образом, статистический ящик сопоставим по вместимости со стандартным ящиком. Преимущество статистического ящика заключается в том, что его содержимое может приблизительно соответствовать номенклатуре ассортиментных позиций, которые фактически продает компания. Тогда как статистический ящик жидкого моющего средства заполнен целыми флаконами, в других случаях статистическая единица может содержать дробные части определенных упаковок, чтобы его общее содержимое соответствовало требуемым суммарным значениям объема или массы. Статистические единицы состоят из фиксированных долей различных ассортиментных позиций. Эти фиксированные доли обеспечивают такое положение вещей, когда изменения цен в статистической единице отражает только изменения в ценах ассортиментных позиций, из которых она состоит. Цена статистической единицы может выражаться либо как совокупная цена набора ассортиментных позиций, составляющих ее, либо через эту совокупную цену, поделенную на общий объем ее составляющих. Первый вариант можно назвать ценой статистической единицы, а второй - штучной ценой статистической единицы. ПРИМЕР. Сливки компании Карла (ССС) продаются в трех форматах: в экономичных однолитровых упаковках, пол-литровых (удобных для хранения в холодильнике) емкостях и в порционных упаковках емкостью 0,05 литра. Карл определяет 12-литровый статистический ящик ССС следующим образом: Две единицы экономичной упаковки = 2 литра (2 х 1,0 литр); девятнадцать упаковок, удобных для хранения в холодильнике = 9,5 литра (19 х 0,5 литра); десять порционных упаковок = 0,5 литра (10 х 0,05). Цены каждого формата и расчет совокупной цены статистической единицы приведены в следующей таблице:
Таким образом, совокупная цена 12-литрового статистического ящика ССС составляет 140 долларов. Цена за литр в рамках статистического ящика - 11,67 доллара. Следует отметить, что цена статистического ящика в 140 долларов выше, чем цена ящика с 12 экономичными упаковками, составляющая 96 долларов. Эта более высокая цена отражает тот факт, что меньшие по вместимости упаковки ССС стоят дороже в пересчете на литры. Если доли SCU в статистическом ящике точно соответствуют фактически проданным долям, тогда цена за литр статистического ящика будет соответствовать цене за литр фактически проданного объема в литрах. ПРИМЕР. Карл продал 10 000 экономичных однолитровых упаковок ССС, 80 000 пол-литровых упаковок, удобных для хранения в холодильнике, и 40 000 порционных упаковок. Какова была средняя цена за литр? (8 долларов х 10 тысяч + 6 долларов х 80 тысяч + 1 доллар х 40 тысяч) (1x10 тысяч + 0,5 х 80 тысяч + 0,05 х 40 тысяч) = 600 долларов / 52 = 11,54 доллара Обратите внимание на тот факт, что у Карла средняя цена за литр (10,34 доллара) меньше, чем цена за литр в его статистическом ящике. Причина этого проста и понятна: тогда как упаковки, удобные для хранения в холодильнике, численно превосходят экономичные упаковки в соотношении почти один к десяти, фактическое соотношение продаж этих SCU составило только восемь к одному. Подобным же образом отметим, что, хотя соотношение порционных и экономичных позиций в статистическом ящике составляет пять к одному, фактическое соотношение их продаж составило только четыре к одному. Компания Карла продала меньше в процентном отношении дорогостоящих (за литр) позиций по сравнению с теми, которые представлены в статистическом ящике. Следовательно, его фактическая средняя цена за литр была меньше, чем цена за литр в статистической единице. В приведенной ниже таблице мы показываем расчет средней цены за единицу как средневзвешенного значения штучных цен и долей штучных продаж трех ассортиментных позиций ССС. Представлены штучные цены и доли штучных (за литр) продаж.
Источники данных, сложности и предостережения В условиях комплексной и меняющейся номенклатуры выпускаемых изделий и при самых разных отпускных ценах, назначаемых различными розничными торговцами, маркетологам необходимо разобраться с рядом методологий расчета средних цен. Важнейшая задача - просто определить, сколько единиц товара было продано по всему рынку и по какой цене. В качестве стандартного метода отслеживания цен маркетологи используют статистические единицы, которые основаны на постоянных долях объема продаж различных SCU в номенклатуре изделий. Обычно доли SCU в статистической единице соответствуют (по крайней мере, приблизительно) исторически сложившейся рыночной конъюнктуре. Однако структура сбыта может меняться. Вследствие этого необходимо быть особенно внимательным при отслеживании указанных долей на эволюционирующих рынках и в условиях меняющейся номенклатуры выпускаемой продукции. Расчет осмысленной средней цены осложнен необходимостью разграничения изменений в номенклатуре продаж и изменений в ценах статистических единиц. В некоторых отраслях трудно сформировать соответствующие единицы для анализа данных о ценах и продажах. В химической промышленности, например, один гербицид может продаваться в самых разных упаковках, для применения с разными распылителями и в разной концентрации. Если учитывать сложность разнообразия цен и ассортимента, предлагаемых конкурирующими розничными магазинами, то расчет и отслеживание средних цен становится непростым делом. Такие же проблемы возникают при расчете инфляции. Экономисты вычисляют уровень инфляции, используя корзину потребительских товаров. Их оценки могут существенно отличаться друг от друга в зависимости от того, какие товары включены в указанную корзину. Также сложно уловить качественное улучшение цифр инфляции. Можно ли сопоставить автомобиль выпуска 2005 года с машиной, сошедшей с конвейера 30 лет назад? Оценивая повышение цен, маркетологам следует иметь в виду, что потребители, которые приобретают большое количество товаров в магазинах, торгующих по сниженным ценам, могут рассматривать такие повышения абсолютно по-иному в сравнении с пенсионерами, которые покупают небольшое количество товаров в ближайшем магазине. Определение стандартной корзины для таких разных потребителей требует неординарных решений. В своем стремлении суммировать совокупность таких повышений цен по всей отрасли экономисты могут рассматривать инфляцию, в сущности, как показатель цены статистической единицы данной отрасли. 3.4. Переменные и постоянные издержки Переменные издержки могут быть включены в суммарные издержки, или выражаться на основе расходов на единицу. Постоянные издержки по определению не изменяются в зависимости от количества проданных или произведенных единиц. Переменные издержки считаются относительно неизменными в расчете на единицу. Совокупные переменные издержки увеличиваются предсказуемо и прямо пропорционально объему штучных продаж. Постоянные издержки, с другой стороны, не изменяются непосредственно в результате краткосрочного повышения или уменьшения штучных продаж. Валовые издержки ($) = Постоянные издержки ($) + Суммарные переменные издержки ($) Суммарные переменные издержки ($) - Объем штучных продаж (#) * Переменные издержки на единицу продукции ($) Маркетологам необходимо иметь представление о том, как затраты распределяются между переменными и постоянными издержками. Такое разграничение имеет первостепенное значение при прогнозировании доходов, полученных в результате различных изменений объема штучных продаж и, таким образом, финансовых последствий предложенных маркетинговых кампаний. Оно также имеет существенное значение для понимания взаимоувязок цен и объемов. Цель: понять, как изменяются издержки с изменением объемов На первый взгляд кажется, что это несложный вопрос. Если в результате проведенной маркетинговой кампании объем продаж увеличился на 10 ООО единиц, то нам следует только узнать, сколько будет стоить поставка этого дополнительного объема товара. Проблема, конечно, заключается в том, что никто на самом деле не знает, как количественные изменения влияют на валовые издержки компании - отчасти потому, что работы компании могут быть чрезвычайно сложными. Компании просто не могут позволить себе держать армию бухгалтеров с целью всегда иметь точный ответ на любой вопрос, возникающий в связи с теми или иными затратами. Вместо этого мы часто используем простую модель динамики затрат, которая вполне подходит для решения большинства задач. Конструкция Стандартное линейное уравнение, Y + mX + Ь, помогает объяснить взаимосвязь между валовыми издержками и объемом штучных продаж. В данном примере Y обозначает валовые издержки компании, m - ее переменные издержки на единицу, X - количество проданных (или произведенных) единиц продукции, a b - постоянные издержки (см. рис. 3.3). Валовые издержки ($) = Переменные издержки на единицу продукции ($) х Количество (#) + Постоянные издержки ($) 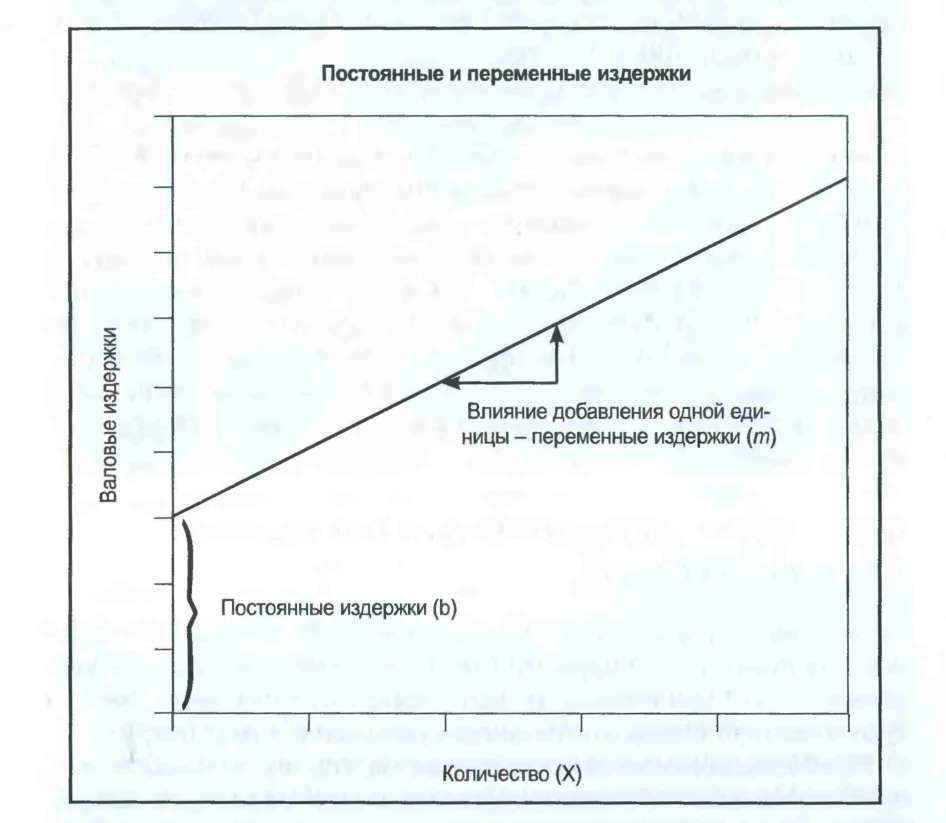 Рис.3.3 Постоянные и переменные издержки Исходя из этого для определения валовых издержек компании на любое заданное количество продукции нам следует только умножить ее переменные издержки на единицу продукции на это количество и добавить постоянные издержки. Чтобы полностью передать последствия постоянных и переменных издержек, было бы полезно разделить этот график на две части (см. рис. 3.4). Постоянные издержки по определению статичны, вне зависимости от объема продаж. Следовательно, на рис. 3.4 они обозначены горизонтальной линией, проведенной поперек графика. Постоянные издержки не изменяются по вертикали, то есть они не добавляют ничего к валовым издержкам по мере увеличения количества проданного товара. Результат умножения переменных единичных издержек на количество товара часто называется совокупными переменными издержками. Переменные издержки отличаются от постоянных тем, что при отсутствии производства их суммарная величина равна нулю. По мере увеличения количества их совокупная величина постепенно растет. Мы можем представить данную модель динамики затрат простой формулой. Валовые издержки ($) = Совокупные переменные издержки ($) + Постоянные издержки ($) Чтобы воспользоваться этой моделью, мы, конечно, должны поместить каждую статью расходов компании в одну или другую категорию. Если затраты не меняются с изменением объема (например, арендная плата), тогда они являются частью постоянных издержек и остаются одинаковыми, вне зависимости от того, сколько единиц товара было произведено или продано. Если затраты изменяются вместе с объемом (например, комиссионные за продажу), тогда они относятся к переменным издержкам. Совокупные переменные издержки ($) = Объем штучных продаж (#) х Переменные издержки на единицу продукции ($) Валовые издержки на единицу продукции. Общие затраты на заданное количество товара можно также выразить в расчете на единицу продукции. Результат можно назвать общими издержками на единицу продукции, единичными валовыми издержками, средними издержками, полными затратами или даже издержками полной нагрузки. Для нашей простой линейной модели издержек валовые издержки на единицу продукции можно рассчитать двумя способами. Наиболее очевидный из них предполагает, что валовые издержки следует поделить на количество единиц продукции. 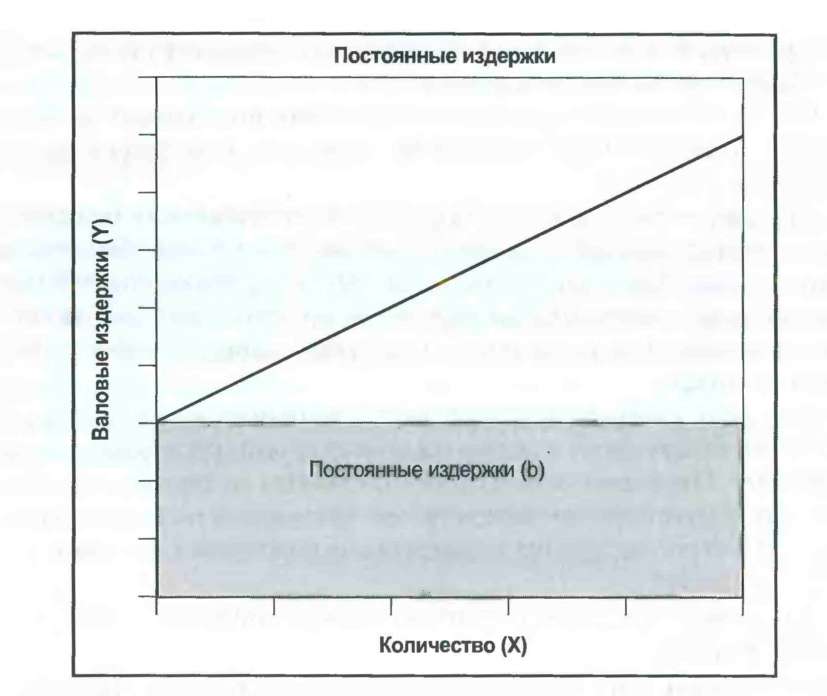 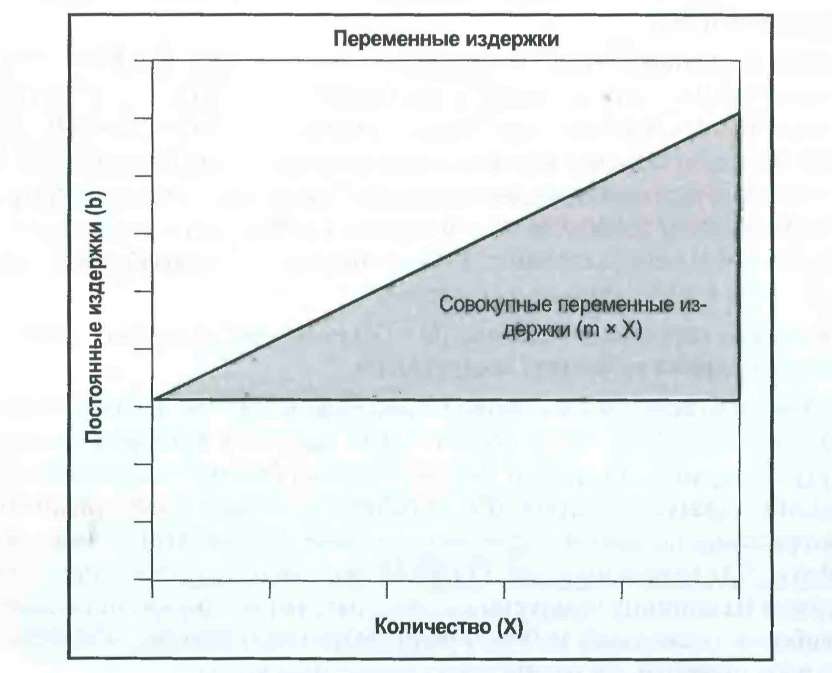 Рис. 3.4. Валовые издержки состоят из постоянных и переменных издержек Общие издержки на еди- = Валовые издержки ($) ницу продукции ($) Количество (#) Это можно отобразить в форме графика, который может рассказать много интересного (см. рис. 3.5). По мере роста количества валовые издержки на единицу продукции (средние расходы на единицу продукции) сокращаются. 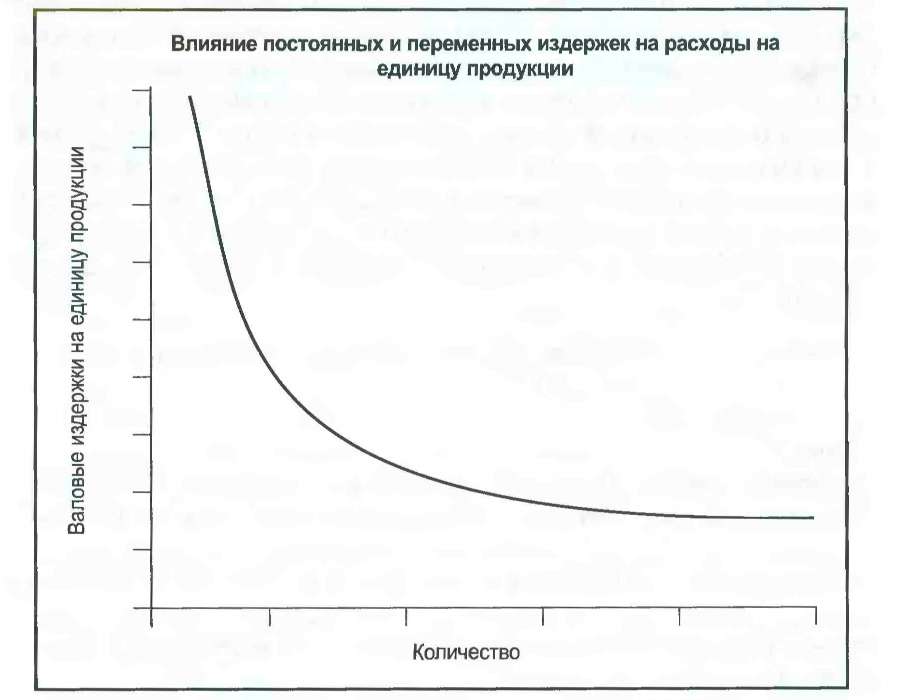 Рис. 3.5. Валовые издержки на единицу продукции в зависимости от объема продаж (типичные ориентировочные расчеты) Форма такой кривой будет меняться по компаниям с разными структурами затрат, но при любых обстоятельствах там, где имеются как постоянные, так и переменные издержки, валовые издержки на единицу продукции будут сокращаться по мере того, как постоянные издержки распределяются среди возрастающего количества единиц продукции. Постатейное распределение постоянных издержек по единицам произведенной продукции приводит нас к еще одной общей формуле для расчета общих издержек на единицу продукции. Валовые издержки на единицу продукции ($) = Переменные издержки на единицу продукции ($) + [Постоянные издержки ($)/Количество (#)] По мере роста количества - то есть по мере распределения постоянных издержек среди увеличивающегося количества единиц продукции - валовые издержки на единицу продукции сокращаются нелинейно3. ПРИМЕР. По мере роста единичных продаж компании ее постоянные издержки сохраняются неизменными на уровне 500 долларов. Переменные издержки на единицу продукции не изменяются и составляют 10 долларов. Совокупные переменные издержки повышаются по мере роста количества продаж. Валовые издержки на единицу продукции (средние валовые издержки) сокращаются по мере постепенного роста штучных продаж и распределения постоянных издержек среди этого увеличивающегося количества продукции. В конечном счете, чем больше производится и продается единиц товара, тем больше валовые издержки на единицу продукции приближаются к переменным издержкам на единицу продукции (см. табл. 3.8). |
