|
|
1. Предмет и задачи методики как научной дисциплины, ее истоки, связь с другими науками
Освоение детьми дошкольного возраста линейных и разветвленных алгоритмов. Алгоритмические игры и упражнения: содержание и организация.
Интуитивно под алгоритмом понимают общепонятное и точное предписание о том, какие действия и в каком порядке необходимо выполнить для решения любой задачи из данного вида однотипных задач.
Освоение дошкольниками алгоритмов способствует упорядочению детского мышления, восприятию определенной последовательности, что выражается в умении планировать свои действия. Так же способствует освоению детьми знаковых систем, схем, моделей, «расшифровке» и познанию логических связей между последовательными этапами какого – либо действия. Выполнение действий по алгоритму в логических играх создает для детей основу совершенствования умений контролировать ход решения игровой и учебной задачи, совершенствованию пространственной ориентировки детей, лучшему освоению ими правил (уличного движения, последовательности действий), успешному осуществлению трудовых и игровых действий, а для педагога – возможность определять затруднения, возникающие у детей.
Действия, выполняемые согласно алгоритму, могут иметь линейную направленность – линейные алгоритмы, повторяться – циклические алгоритмы, они могут разветвляться, если алгоритм предусматривает два варианта ответа: «да» и «нет» - разветвленные алгоритмы. Алгоритмы рассматриваются в качестве средства обучения.
В младшем возрасте идет накопление представлений последовательности выполнения игровых действий по условному знаку – стрелке, показывающей направление движения в пространстве; порядок расположения предметов, геометрических фигур. В этом возрасте дошкольники применяют линейный алгоритм. В среднем возрасте дошкольниками используются простейшие алгоритмы это линейные и разветвленные. В старшем возрасте дошкольники пользуются линейными, простыми разветвленными и циклическими алгоритмами. В этом возрасте они самостоятельно составляют алгоритмы, выполняют заданные им действия, поясняют последовательность.
Примеры игр с использованием линейных алгоритмов: «Выращиваем дерево» в игре используются рисунки с изображением геометрических фигур (квадрат, прямоугольник, треугольник, круг) и стрелки, которые отходят от каждой фигуры, указывают, что, после чего растёт на нашем дереве. В рисунках отображены правила игры. Детям предлагается задание вырастить необычное дерево, на котором растут геометрические фигуры. Нужно внимательно смотреть на рисунки и следовать по стрелкам при выкладывании следующей фигуры. Один из играющих кладёт на стол какую-нибудь фигуру, второй – стрелку и следующую фигуру в соответствии с правилом. Так продолжается до тех пор пока дерево перестанет расти или у игроков закончатся фигуры.
Примеры игр с использованием разветвлённых алгоритмов: «Вычислительные машины» в игре понадобится набор цифр и вычислительная машина «блок-схема алгоритма». Играют две команды, одна даёт задание, а вторая выполняет. Даются примерно такие задания по алгоритму: 1) сравни числа; 2) если первое число меньше второго, (да) идём влево и выполняем следующее задание +2; 3) если «нет», идём вправо и выполняем другое условие -2; 4) машина выдаёт ответ (красный круг). Игра продолжается с новыми числами.
Умение применять разного рода алгоритмы, тем более умение предвидеть и обосновывать возможные результаты их применения — признак формирования свойственного для математика стиля мышления.
|
Познание дошкольниками циклических алгоритмов. Содержание и организация игр и упражнений.
Освоение дошкольниками алгоритмов способствует упорядочению детского мышления, восприятию определенной последовательности, что выражается в умении планировать свои действия. Выполнение действий по алгоритму в логических играх создает для детей основу совершенствования умений контролировать ход решения игровой и учебной задачи, совершенствованию пространственной ориентировки детей, лучшему освоению ими правил (уличного движения, последовательности действий), успешному осуществлению трудовых и игровых действий, а для педагога – возможность определять затруднения, возникающие у детей.
Действия, выполняемые согласно алгоритму, могут иметь линейную направленность – линейные алгоритмы, повторяться – циклические алгоритмы, они могут разветвляться, если алгоритм предусматривает два варианта ответа: «да» и «нет» - разветвленные алгоритмы. Алгоритмы рассматриваются в качестве средства обучения.
Пример циклического алгоритма: игра «Преобразование слов», моделирующая понятие алгоритм преобразования слов в данном алфавите.
В этой игре, а по существу серии игр, буквы и слова необычные. Используется двухбуквенный алфавит, состоящий из двух различных геометрических фигур, например квадратика и кружочка. Словами мы называем конечные цепочки из квадратиков и кружочков. Любое слово в алфавите преобразовывается по приведенным правилам, отображённом на рисунке: если в заданном слове имеется квадратик, расположенный левее кружочка, то, согласно правилу 1, их нужно поменять местами; если во вновь полученном слове опять имеется квадратик, расположенный левее кружочка, нужно опять их поменять местами и т.д.; правило 1 применяется столько раз, сколько возможно, т. е. пока не получится слово, в котором уже нет квадратика, расположенного левее кружочка, или в котором все кружочки лежат левее всех квадратиков; затем переходим к применению правила 2, а именно: если имеются два рядом стоящих кружочка, их удаляют, и правило 2 применяется столько раз, сколько возможно, т. е. пока не получится слово, в котором нет двух рядом стоящих кружочков; затем переходим к применению правила 3, а именно: если имеются два рядом стоящих квадратика, их удаляют, и это правило применяется столько раз, сколько возможно, т. е. пока не получится слово, в котором нет двух рядом стоящих квадратиков. Полученное слово является результатом преобразования исходного слова по заданным правилам и способу их применения, определяющим вместе некоторый алгоритм преобразования слов в данном алфавите.
Как показывает опыт обучения, повторив эту игру несколько раз для различных «слов», дети 5—6 лет в состоянии заранее правильно определить, какие вообще могут оказаться результаты сокращения «слов» по заданным правилам: кружочек и квадратик, или один кружочек, или один квадратик, или «ничего» (это «ничего» называют «пустым словом»).
П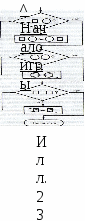 риведенные выше правила игры вместе с процедурой их применения могут быть изображены блок-схемой (илл. 23). риведенные выше правила игры вместе с процедурой их применения могут быть изображены блок-схемой (илл. 23).
Умение применять разного рода алгоритмы, тем более умение предвидеть и обосновывать возможные результаты их применения — признак формирования свойственного для математика стиля мышления.
|
Современные требования к отбору содержания математического развития дошкольников.
Математическая подготовка детей к школе предполагает не только усвоение детьми определённых знаний, формирование у них количественных пространственных и временных представлений. Наиболее важным является развитие у дошкольников мыслительных способностей, умение решать различные задачи. Воспитатель должен знать, не только как обучать дошкольников, но и то, чему он их обучает, то есть ему должна быть ясна математическая сущность тех представлений, которые он формирует у детей. Широкое использование устного народного творчества так же важно для пробуждения у дошкольников интереса к математическим знаниям, совершенствования познавательной деятельности, общего умственного развития.
Дети четырёх лет активно осваивают счёт, пользуются числами, осуществляют элементарные вычисления по наглядной основе и устно, осваивают простейшие временные и пространственные отношения, преобразуют предметы различных форм и величин. Ребёнок, не осознавая того, практически включается в простую математическую деятельность, осваивая при этом свойства, отношения, связи и зависимости на предметах и числовом уровне.
Объём представлений следует рассматривать в качестве основы познавательного развития. Активность ребёнка, направленная на познание, реализуется в содержательной самостоятельной игровой и практической деятельности, в организуемых воспитателем познавательных развивающих играх.
Взрослый создаёт условия и обстановку, благоприятные для вовлечения ребёнка в деятельность сравнения, сосчитывания, воссоздания, группировки, перегруппировки и т.д. При этом инициатива в развёртывании игры, действия принадлежит ребёнку. Воспитатель вычленяет, анализирует ситуацию, направляет процесс её развития, способствует получению результата.
Ребёнка окружают игры, развивающие его мысль и приобщающие его к умственному труду. Например, игры из серии: "Логические кубики" , "Уголки", "Составь куб" и другие; из серии: "Кубики и цвет", "Сложи узор", "Куб-хамелеон" и другие.
Играя и занимаясь с детьми, воспитатель способствует развитию у них умений и способностей:
- оперировать свойствами, отношениями объектов, числами; выявлять простейшие изменения и зависимости объектов по форме, величине;
- сравнивать, обобщать группы предметов, соотносить, вычленять закономерности чередования и следования, оперировать в плане представлений, стремиться к творчеству;
- проявлять инициативу в деятельности, самостоятельность в уточнении или выдвижении цели, в ходе рассуждений, в выполнении и достижении результата;
- рассказывать о выполняемом или выполненном действии, разговаривать со взрослыми, сверстниками по поводу содержания игрового (практического ) действия.
Пятилетки проявляют высокую познавательную активность, они буквально забрасывают старших разнообразными вопросами об окружающем мире. Исследуя предметы, их свойства и качества, дети пользуются разнообразными обследовательскими действиями: умеют группировать объекты по цвету, форме, величине, назначению, количеству; умеют составить целое из 4-6 частей; осваивают счёт.
Линейно-концентрический принцип, который лежит в основе формирования элементарных математических представлений, предполагает в каждом возрастном этапе повторение на более высоком уровне того, что было освоено на предыдущей ступени, и дальнейшее продвижение вперед. Однако в каждом году обучения выделяется одно главное направление. Во второй младшей группе — формирование представлений о равенстве и неравенстве групп по количеству входящих в них предметов, в средней группе — формирование представлений о числах в пределах 5, в старшей — формирование представлений о числах и отношениях между последовательными числами в пределах 10.
|
64. Планирование процесса формирования и развития математических представлений у детей в дошкольных учреждениях.
Задачи развития у детей элементарных математических представлений не могут быть решены без правильного планирования и учета работы. Планирование — один из способов управления процессом формирования элементарных математических представлений у детей. План дает возможность целенаправленно и систематически распределять по времени программные задачи и пути их осуществления. Кроме того, план определяет отчетную документацию, по которой можно судить о состоянии и результатах педагогического процесса. Для правильного планирования и постановки работы по развитию элементарных математических представлений у детей воспитатель должен: 1) хорошо знать программу в целом и программу той возрастной группы, в которой он работает в текущем учебном году; 2) знать возрастные и индивидуальные особенности своих воспитанников; 3) уметь руководствоваться дидактическими принципами при планировании и организации обучения; 4) знать методические основы развития у детей математических представлений; 5) постоянно повышать квалификацию, быть в курсе современных достижений науки и практики воспитания дошкольников.
В практике работы дошкольных учреждений имеют место два вида планирования: перспективное и календарное. Перспективные планы относятся к числу методических материалов дошкольного учреждения, поэтому разрабатываются, как правило, воспитателями группы при непосредственном участии руководства дошкольного учреждения.
Перспективный план составляется обычно на текущий квартал. В нем предусматриваются лишь образовательные задачи. В его содержание входит распределение программных задач в строго определенной системе. Возможно применение двух способов перспективного планирования. Первый — распределение программных задач по определенной теме (количество и счет, величина и др.). Второй — комплексное распределение программных задач всего раздела «Развитие элементарных математических представлений». При комплексном распределении программного материала следует иметь в виду, что содержание занятий, на которых решаются новые задачи, следует ограничивать 1—2 темами в младшей и средней группах и 2—3 темами в старшей группе. Занятия на повторение программного материала могут включать от 3 до 5 программных задач, как правило, взаимосвязанных между собой. В перспективном плане должны быть представлены все виды работ по усвоению программных задач.
В календарном плане перспектива, намеченная на квартал, находит свое конкретное воплощение. Разрабатывая его, следует учесть, что занятия по математике проводятся в установленный день один раз в неделю во всех дошкольных группах.
Календарный план занятий содержит:
1. Программные задачи: а) образовательные, б) развивающие, в) воспитательные.
Образовательные задачи берутся в основном из перспективного плана, нередко требуется их конкретизация и уточнение.
Развивающие задачи предусматриваются с целью развития речи, мышления, других психических процессов. Планировать их необходимо, так как обязательным требованием к каждому занятию по математике является не только сообщение знаний, но и развитие умственных способностей детей.
Воспитательные задачи планируются с целью формирования у детей дисциплинированности, положительного отношения к учебной деятельности и т. п. Они предусматриваются на длительный период работы, поэтому указывать их в каждом занятии не обязательно.
2. Задачи индивидуальной работы с отдельными детьми планируются по тем же трем направлениям. Индивидуальную работу следует планировать в определенной системе на каждом занятии.
3. Дидактический материал.
|
65. Диагностика уровня освоенности математических представлений у дошкольников.
Одним из важных показателей спец-ой (матем-кой) готовности является наличие у дошкольников определенных знаний, умений и навыков. Для педагога дошкольного учреждения особое значение приобретает выявление этого уровня перед поступлением детей в школу. Этому способствуют диагностические тесты: индивидуальные беседы, дидактические игры и упражнения с детьми, выполнение ими специальных заданий и т. п. При этом следует выделить основные компоненты готовности ребенка к усвоению математики в школе: мотивационный, содержательный и процессуальный.
Мотивационный компонент готовности включает: положительное отношение к школе и учебной деятельности в целом; интерес к математической стороне действительности; желание изучать математику.
Содержательный компонент включает прежде всего знания детей в соответствии с программой детского сада: объем и качество математических знаний: осознанность, прочность запоминания, возможность усвоения их в самостоятельной деятельности (гибкость); особенности развития речи (усвоение математической терминологии); уровень познавательной активности в целом.
Процессуальный компонент — это: специальные умения (считать, измерять, вычислять и др.); умения и навыки учебной деятельности.
Изучать уровень готовности детей к обучению в школе можно с помощью как группового, так и индивидуального обследования.
Индивидуальное обследование дает возможность воспитателю создать представление об особенностях мышления, речи детей, общем уровне знаний и специальной математической подготовке.
В качестве диагностических (тестовых) упражнений можно использовать задания такого типа.
Ребенку предлагают ответить на вопросы: «Когда ты пойдешь в школу? Что ты знаешь о школе? Хочется ли тебе учиться в школе?» Любишь ты занятия по математике? А как ты думаешь, что делают ученики на уроках математики?»
По степени успешности выполнения задания можно выявить уровень математической готовности ребенка к школьному обучению. Эти данные следует дополнять систематическими наблюдениями, индивидуальными беседами с детьми.
Для оценки степени готовности детей к обучению в школе в условиях разноуровневой дифференциации ею разработаны критерии:
степень психосоциальной зрелости (по тестам-беседе);
уровень школьной зрелости по тестам Керна—Йрасека, Векслера;
уровень умственной работоспособности по корректурным пробам;
уровень развития восприятия;
уровень развития памяти;
уровень развития мышления.
В соответствии с показателями условно можно выделить три уровня готовности детей к школе.
К первому уровню следует отнести готовность детей, которые хорошо усвоили программные требования предыдущих групп, имеют хорошие навыки в счетной деятельности, обследовании, измерении, делении целого на части, решении задач и т. п.
Ко второму уровню можно отнести готовность детей, которые овладели программой данной группы; имеют определенные навыки в счетной деятельности, измерении величин, делении целого на части. Вместе с тем у них недостаточно развита умственная деятельность: им трудно объяснить выбор арифметического действия, обобщать и классифицировать; самоконтроль у этих детей неустойчивый, они не проявляют интереса к учебной деятельности; математический словарь их беден; самооценка чаще всего занижена, иногда завышена.
К третьему уровню относится готовность детей, которые слабо усвоили программу по математике. Эти дети имеют некоторые навыки в выполнении операций счета, но во всех других видах математической деятельности имеют слабые навыки или вообще их не имеют.
Педагогическую работу по подготовке детей к школе следует направить на полную ликвидацию третьего, низшего, уровня сформированности математических знаний, умений и навыков и на достижение у них достаточно качественной математической готовности к школе.
|
66.Учебно-игровая деятельность математического содержания и формы ее организации в дошкольных учреждениях.
Полноценное математическое развитие обеспечивает организованная, целенаправленная деятельность, в ходе которой воспитатель продуманно ставит перед детьми познавательные задачи, помогает найти адекватные пути и способы их решения. Формирование элементарных математических представлений у дошкольников осуществляется на занятиях и вне их, в детском саду и дома. Занятия являются основной формой развития элементарных математических представлений в детском саду. На них возлагается ведущая роль в решении задач общего умственного и математического развития ребенка и подготовки его к школе. Занятия по формированию элементарных математических представлений у детей, строятся с учетом общедидактических принципов: научности, системности и последовательности, доступности, наглядности, связи с жизнью, индивидуального подхода к детям и др. Во всех возрастных группах занятия проводятся фронтально, т. е. одновременно со всеми детьми. Полученные детьми знания и умения закрепляются в повседневной жизни: в играх, игровых упражнениях, на прогулках и т.д. В практике работы по формированию элементарных математических представлений сложились следующие типы занятий:
1) занятия в форме дидактических игр;
2) занятия в форме дидактических упражнений;
3) занятия в форме дидактических упражнений и игр.
Выделение их условно и зависит от того, что является ведущим на занятии: дидактическая игра, дидактический материал и деятельность с ним или сочетание того и другого. При любом типе занятия воспитатель активно руководит процессом усвоения детьми знаний и навыков.
Занятия в форме дидактических игр широко применяются в младших группах. В этом случае обучение носит незапрограммированный, игровой характер. Мотивация учебной деятельности также является игровой. Воспитатель пользуется в основном методами и приемами опосредованного педагогического воздействия: применяет сюрпризные моменты, вводит игровые образы, создает игровые ситуации на протяжении всего занятия, в игровой форме его заканчивает. Упражнения, с дидактическим материалом хотя и служат учебным целям, приобретают игровое содержание, целиком подчиняясь игровой ситуации.
Занятия в форме дидактических упражнений используются во всех возрастных группах. Обучение на них приобретает практический характер. Воспитатель применяет приемы прямого обучающего воздействия на детей: показ, объяснение, образец, указание, оценка и т. д. В младшем возрасте учебная деятельность мотивируется практическими и игровыми задачами (например, дать каждому зайцу по одной морковке, чтобы узнать, поровну ли их; построить лесенку из полосок разной длины для петушка и т. д.), в старшем возрасте - практическими или учебными задачами (например, измерить полоски бумаги и отобрать определенной длины для ремонта книг, научиться измерять длину, ширину, , высоту предметов и т. д.).
Игровые элементы в разных формах могут включаться в упражнения с целью развития предметно-чувственной, практической, познавательной деятельности детей с дидактическим материалом.
Т.О. к формам формирования у дошкольников математических способностей относятся занятия и дидактические игры, в которых воспитатель активизирует слуховой и зрительный анализаторы дошкольников.
|
67.Индивидуальная и самостоятельная деятельность математической направленности, условия ее организации в дошкольных учреждениях.
Индивидуальная деятельность математической направленности заключается в том, что ребенок приобретает знания, выполняет различные задания, имея возможность получения при этом непосредственной или косвенной помощи со стороны взрослого. Индивидуальное обучение обеспечивает накопление личного опыта, развитие самостоятельности и активности ребенка, переживание положительных эмоций от общения непосредственно с педагогом. Именно при индивидуальном обучении сотрудничество ребенка со взрослым позволяет достигать цели. Это связано с тем, что, обучая одного ребенка, взрослый легко может увидеть его «зону ближайшего развития».
Дифференциация обучения осуществляется по следующим критериям: способностям или неспособностям к обучению, интересам, объему материала и степени его сложности, степени самостоятельности и темпу продвижения в обучении.
Индивидуальная работа может осуществляться в различных повседневных учебных ситуациях, т. е. в процессе организации разных режимных моментов: во время приема детей утром, в процессе одевания, раздевания, умывания, а также при руководстве деятельностью дежурных, играх и др. Так, воспитатель предлагает ребенку обратить внимание на значки (геометрические фигуры) на шкафчиках для детской одежды, на обувь (правый — левый ботинок), на размещение одежды в шкафчике (на верхней полочке лежит шапка, внизу стоят ботинки) и т. д.
На каждом коллективном занятии имеет место работа с отдельными детьми. Это может быть временное снижение требований, активная непосредственная помощь со стороны воспитателя детям, которые в ней нуждаются. Или, наоборот, предложение некоторым детям сложных, проблемных заданий с учетом их возможностей и интересов.
Закрепление пройденного материала осуществляется в самостоятельной деятельности детей. Для организации самостоятельной деятельности детей очень важно создать соответствующие условия, т.е. развивающую среду.
В группе раннего возраста нужно иметь в группе дидактический столик для развития сенсорных способностей и совершенствования моторики. Комплектация стола: пирамидки, вкладыши разного типа, разноцветные счеты, горки для прокатывания предметов, набор объемных форм.
В младшей группе целесообразно отвести специальное место для игротеки, обозначив его ярким плакатом математической направленности (с использованием цифр-образов, форм, предметов разного размера). Там должны быть собраны игры, направленные на развитие сенсорного восприятия, мелкой моторики, воображения, речи. Играя, ребенок уточняет представления о свойствах предметов — форме, величине, материале.
В математическом центре детей средней группы используются материалы и пособия, которые позволяют организовать разнообразную практическую деятельность детей: пересчитать, соотнести, сгруппировать, упорядочить. В математической игротеке могут быть размещены различные варианты книг, рабочих тетрадей для рассматривания и выполнения заданий.
В старшей группе математический центр пополняется дидактическими, развивающими и логико-математическими играми, направленными на развитие логического действия сравнения, логических операций классификации, сериации, узнавание по описанию, воссоздание, преобразование, ориентировку по схеме, модели; на осуществление контрольно-проверочных действий («Так бывает?», «Найди ошибки художника»); на следование и чередование и др.
|
68.Математическое развитие ребенка в условиях домашнего воспитания.
Источником элементарных математических представлений ребёнка является окружающая реальная действительность, которую ребенок познает в процессе своей разнообразной деятельности, в общении со взрослыми и под их обучающим руководством.
С первых дней жизни ребенка окружают люди, которые воздействуют на его развитие, и с которыми он устанавливает эмоциональный контакт. Окружают ребенка и многочисленные вещи, обладающие различными свойствами и качествами.
В процессе разнообразной перцептивной и продуктивной деятельности у детей с раннего возраста начинают формироваться представления об окружающем их мире: о различных признаках и свойствах предметного мира — цвете, форме, величине, о пространственном расположении предметов, об их количестве, а также об отношениях людей (к самому ребенку, друг к другу, к окружающим вещам и т. д.). Постепенно накапливается сенсорный опыт, который явится основой формирования элементарных математических представлений и первых понятий.
Ребенок рано также начинает различать предметы по размеру, цвету, форме, по пространственному расположению и по другим признакам. Подражая взрослым, он пытается примитивно измерять предметы, сначала накладывая одни на другие, затем на глаз и с помощью условных общепринятых мер измерения.
Как только ребенок сам начинает передвигаться, он действенно знакомится с пространством и пространственными отношениями между вещами: он то приближается (не без труда) к интересующим его вещам, то удаляется от них. Оказывается, одни предметы находятся перед ребенком, другие—сзади него или справа, слева. Обучение позволяет малышу рано усвоить значение таких слов, как ближе —дальше и др. Ребенок практически и сам ориентируется в пространственном расположении предметов, а под руководством взрослого учится и словесно определять их местоположение сначала по отношению к себе, а затем и по отношению к другим предметам (справа от куклы — мишка, а слева от нее — зайчик).
Со временем у ребенка создается элементарное представление о близком и далеком пространстве, хотя еще весьма конкретное (сад, в котором он гуляет,— близко, а работа папы — очень далеко). Опираясь на подобные конкретные представления, в результате личного опыта и обучения взрослыми, ребенок постепенно приходит к более широким обобщениям; в старшем дошкольном возрасте мерилом пространства становится время («Черное море так далеко, что надо ехать поездом или лететь самолетом»).
| |
|
|
 Скачать 0.65 Mb.
Скачать 0.65 Mb.