Главная страница
Навигация по странице:

  • Восстановить энтимему: Курение – это яд, следовательно, курение – вред!

  • Сделать вывод и проверит ь правильность. Определить вид умозаключения.

  • Привести пример метода сопутствующих изменений.

  • Правильно ли произведено деление понятия: Улица состоит из до мов, дороги, сквера, светофора.

  • Билет

  • Восстановить энтимему: Красный – это цвет. Некоторые телефоны – красные.

  • Определить вид и проверить умозаключение, приведя к традиционным типам. Роза бывает либо жёлтая, либо красная, либо розовая, либо белая. А роза белая, значит, она не жёлтая, не красная, не розовая.

  • Обосновать модус ААА I фигуры.

  • Правильно ли дано определение (если – нет, почему, указать ошибки) Опиум употребляют потому, что он имеет усыпляющую силу, а усыпляющую силу он имеет потому, что он усыпляет.

  • Билет 5.

    		•

    мои. Билет Привести пример рассуждения по методу остатков


    Скачать 0.95 Mb.
    НазваниеБилет Привести пример рассуждения по методу остатков
    Анкормои.docx
    Дата02.05.2017
    Размер0.95 Mb.
    Формат файлаdocx
    Имя файламои.docx
    ТипДокументы
    #6478
    страница2 из 12
    1   2   3   4   5   6   7   8   9   ...   12

    Противопоставить предикату: Лимоны – это китайские яблоки.

    S+ Р-

    A: Лимоны – это китайские яблоки
    Противопоставление предикату – преобразование, в котором мы выявляем отношение понятия, противоречащего предикату к субъекту.

    _

    SAPPES _

    P+ S+

    Е: Все не китайские яблоки не есть лимоны.

    1. Восстановить энтимему: Курение – это яд, следовательно, курение – вред!

    S+ М-

    А: Курение есть яд. Меньшая посылка.
    S+ P-

    А: Курение есть вред.

    Итак, мы видим, что пропущена большая посылка, т.к. предикат заключения, должен находиться в большей посылке, а таковой мы не наблюдаем. По расположению среднего термина в меньшей посылке на месте предиката, мы можем предположить, что собеседник рассуждал по I или II фигуре.

    Таким образом получаем:

    М+ Р-

    А: Яд есть вред. Большая посылка.

    S+ М-

    А: Курение есть яд. Меньшая посылка.
    S+ P-

    А: Курение есть вред.
    Модус ААА соответствует I фигуре, правила терминов, посылок и фигур не нарушены, следовательно энтимема правильна.


    1. Сделать вывод и проверить правильность. Определить вид умозаключения. Если я пойду в кино - мне будет интересно, если я пойду в цирк – весело, если я пойду на работу, то мне будет скучно. А я пойду либо в кино, либо в цирк, либо на работу, значит…

    Условно-разделительное умозаключение по схеме логики высказываний.

    Вывод: значит либо мне будет интересно, либо весело, либо скучно.

    А - пойду в кино

    В - мне будет интересно

    С - пойду в цирк

    D - мне будет весело

    Е - пойду на работу


    ((АВ) ˄(СD)˄ (ЕF) ˄(AѶCѶE)(BѶDѶF)
    F - мне будет скучно


    Метод от противного:

    Допустим наша формула ложна. Мы нашли значения переменных, при которых данная формула принимает значение лжи. Следовательно наше предположение верно, формула ложна.


    ((АВ) ˄(СD)˄ (ЕF) ˄(AѶCѶE)(BѶDѶF)
    л

    и

    и

    и

    л

    и/л и

    и

    и/л и

    и

    и л л

    л и л

    л л и

    и/л и

    и и и


    1. Привести пример метода сопутствующих изменений.

    А1ВС – d1

    А2ВС – d2

    А3ВС – d3_____________________________

    Вероятное изменение А влечет изменение d.


    1. Правильно ли произведено деление понятия: Улица состоит из домов, дороги, сквера, светофора.

    Говорить о делении понятия некорректно, т.к. произведено расчленение предмета на части, а не деление.
    Билет 4.

    1. Привести пример постепенного доказательства.

    2. Правильно ли: У некоторых мужчин есть усы, следовательно, не верно, что все мужчины не имеют усов.

    S- P-

    J: Некоторые мужчины есть имеющие усы.

    S+ Р+

    E: Все мужчины не есть не имеющие усов.
    При помощи логического квадрата установим отношения между нашими суждениями: суждения вида J и Е находятся в отношении противоречия. Противоречащие суждения не могут быть ни одновременно ложными, ни одновременно истинными, т.е. если одно ложно, то другое истинно с необходимостью и если одно истинно, то другое ложно с необходимостью. Следовательно, если суждение вида J истинно, то суждение вида Е с необходимостью ложно, значит рассуждение верно.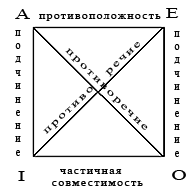

    0000sp5p


    1. Восстановить энтимему: Красный – это цвет. Некоторые телефоны – красные. (не уверена)

    М+

    А: Красный есть цвет.

    М-

    J: Некоторые телефоны есть красные.
    По расположению среднего термина (в одной посылке на месте субъекта, в другой - предиката), мы можем предположить, что собеседник рассуждал по I или IV фигуре. Пропущено заключение, т.к. мы встречаем средний термин 2 раза.

    Таким образом:
    М+ Р-

    А: Красный есть цвет. Большая посылка.

    S- М-

    J: Некоторые телефоны есть красные. Меньшая посылка.
    S- Р-

    J: Некоторые телефоны есть имеющие цвет.
    Мы видим, что рассуждение идёт по I фигуре, модус АJJ соответствует данной фигуре. Правила посылок, терминов и фигур не нарушены, следовательно, энтимема верна.

    1. Определить вид и проверить умозаключение, приведя к традиционным типам. Роза бывает либо жёлтая, либо красная, либо розовая, либо белая. А роза белая, значит, она не жёлтая, не красная, не розовая.

    AѶВѶСѶD

    D
    A˄B˄C

    А – роза – жёлтая

    В – роза – красная

    С – роза – розовая

    D – роза – белая

    ((AѶВѶСѶD)˄D)(A˄B˄C)

    ((AѶВѶСѶD)˄D)(A˄B˄C)

    Разделительно-категорическое умозаключение по схеме логики высказываний.

    Метод от противного:

    ((AѶВѶСѶD)˄D)(A˄B˄C)

    Допустим наша формула ложна. Но тогда возникает противоречие. Значит наше предположение не верно, формула тождественно истинна.


    л

    и

    л

    л л л и

    и

    и и и

    и


    А
    В
    С
    D
    A
    B
    C
    D
    AѶВѶСѶD
    (AѶВѶСѶD)˄D
    A˄B˄C
    ((AѶВѶСѶD)˄D)(A˄B˄C)

    и
    и
    и
    и
    л
    л
    л
    л
    л
    л
    л
    и

    и
    и
    и
    л
    л
    л
    л
    и
    л
    л
    л
    и

    и
    и
    л
    и
    л
    л
    и
    л
    л
    л
    л
    и

    и
    и
    л
    л
    л
    л
    и
    и
    л
    л
    л
    и

    и
    л
    и
    и
    л
    и
    л
    л
    л
    л
    л
    и

    и
    л
    и
    л
    л
    и
    л
    и
    л
    л
    л
    и

    и
    л
    л
    и
    л
    и
    и
    л
    л
    л
    л
    и

    и
    л
    л
    л
    л
    и
    и
    и
    и
    л
    л
    и

    л
    и
    и
    и
    и
    л
    л
    л
    л
    л
    л
    и

    л
    и
    и
    л
    и
    л
    л
    и
    л
    л
    л
    и

    л
    и
    л
    и
    и
    л
    и
    л
    л
    л
    л
    и

    л
    и
    л
    л
    и
    л
    и
    и
    и
    л
    л
    и

    л
    л
    и
    и
    и
    и
    л
    л
    л
    л
    л
    и

    л
    л
    и
    л
    и
    и
    л
    и
    и
    л
    л
    и

    л
    л
    л
    и
    и
    и
    и
    л
    и
    и
    и
    и

    л
    л
    л
    л
    и
    и
    и
    и
    л
    л
    и
    и

    1. Обосновать модус ААА I фигуры.


    В первой фигуре простого категорического силлогизма средний термин в большей посылке находится на месте субъекта, а в меньшей - на месте предиката. Первая фигура имеет следующую структуру:

    M-Р
    S-М
    _____
    S-P
    Наша задача обосновать модус ААА для данной фигуры, сделаем это с помощью примера:

    M+ P-

    А: Все люди - смертны. Большая посылка.

    S+ M-

    А: Все греки - люди. Меньшая посылка.
    S+ P-

    А: Все греки – смертны.
    Правила I фигуры.


    1. Большая посылка – всегда общее суждение.

    2. Меньшая посылка – всегда утвердительное суждение.


    Если большая посылка суждение вида А (как в нашем примере), то предикат заключения нераспределён. Если предикат заключения нераспределен, значит, что заключение суждения вида А или J. В нашем примере заключения вида А. Если заключение вида А, то меньшая посылка тоже должна быть вида А, т.к. субъект заключения есть субъект меньшей посылки, а т.к. в заключении субъект распределен, то он должен быть распределен в меньшей посылке (термин нераспределённый в посылке не может быть распределён в заключении), следовательно, меньшая посылка должна быть вида А.
    Следовательно, можно сделать вывод, что модус ААА соответствует I фигуре, т.к. не нарушены правила, терминов, посылок и фигур.


    1. Правильно ли дано определение (если – нет, почему, указать ошибки)? Опиум употребляют потому, что он имеет усыпляющую силу, а усыпляющую силу он имеет потому, что он усыпляет.


    Определение дано не верно, т.к.:

    • Объёмы Dfd и Dfn нетождественны. Определение узкое. Вместо видообразующих признаков указывается только функция. Определение не содержит родового понятия.

    • Определение содержит тавтологию (усыпляющую силу имеет потому, что усыпляет) – ВОЗМОЖНО, НЕВЕРНО!


    Билет 5.

    1. Правильно ли дано определение: Ты – не Бог.


    Определение дано не верно, т.к.:

    • Определение содержит только отрицание, нет указания на универсум и существенные признаки, есть только противопоставление.



    1. 1   2   3   4   5   6   7   8   9   ...   12

    написать администратору сайта