Лекции по теории композиции. 19211922 Методическая записка к курсу Теория композиции

• Название: Лекции по теории композиции. 19211922 Методическая записка к курсу Теория композиции
• Анкор: Favorsky LTN.doc
• Дата: 26.11.2017
• Размер: 33.41 Mb.
• Имя файла: Favorsky LTN.doc
• Тип: Лекции; #10447
• страница: 18 из 42

Какое же из этих изображений может быть единицей пространства, может быть кирпичом пространственного здания?

По-видимому, не профильное, а объемное, но объемное не перешедшее, а незаметно переходящее в пространственное изображение.

В профильном и контурном изображении мы не имеем ясного отношения к вертикали и к горизонтали, но поэтому там все направления на поверхности более или менее соизмеримы.

В объемном предметном изображении с фасной осью вертикаль есть рост предмета, особенно если это человек; горизонталь будет шириной предмета. Но вертикаль может незаметно приобрести качества пространственной вертикали, и тогда она даст абсолютную величину пространственной вертикали, а горизонталь, которая в пространствен ном изображении со зрительной осью потеряет всякую конкретность и соизмеримость, будет почти не воспринята, так как пространство будет образовано движением вертикали, в объемном изображении будет существовать как мера предмета, но может легко приобрести некоторый оттенок внутренней беспредельности.

Итак, изображение с объемной осью, которое приобретает некоторое зрительное значение, будет тем изображением предмета, которое может стать единицей пространства, кирпичом пространственного здания.

Примерами этих изображений предмета очень богато искусство Ренессанса.

Изображение контурное, не имеющее оси объема, мы можем встретить в раннем христианском искусстве, в изображении доброго пастыря и в первых распятиях, где довольно цветной контур имеет главное значение, а изображение отнюдь не строго симметрично.

Джотто, Мазаччо, Гирландайо, Перуджино, Рафаэль и другие могут служить примерами изображения объемного, имеющего центральную ось вращения.

И, наконец, Микеланджело дает пример изображения предмета, у которого центральная объемная ось превратилась в ось зрительную и у которого предмет, таким образом, стал сам замкнутым пространством, пространственным миром.

Но у Гирландайо, у Джотто, у Мазаччо и Рафаэля мы встречаем предмет, который не стал миром, но которым можно орудовать как единицей, как кирпичом, чтобы строить пространство.



ШЕСТНАДЦАТАЯ








Операции над объемом

Симметрия. Какое изображение предмета пригодно

для постройки пространства
Итак, в прошлый раз мы разобрали возможные изображения предметов и взвешивали их относительно того, какие из них дают образ обособленного предмета и какое из этих изображений пригодно для того, чтобы строить им пространственное здание.

При этом рассмотрении мы пришли к тому, что объемное изображение с объемной осью, иногда несколько переходящее в пространственно-зрительное изображение со зрительной осью, пригоднее всего для той задачи, которую мы думали усмотреть в Ренессансе.

Объемное изображение уже пригоднее потому, что, строя предметом пространство, мы должны его двигать по изобразительной плоскости, а это было бы немыслимо, если бы предмет приобрел значение зрительного центра, главного или дополнительного, тогда бы его место было бы безусловно и к его путешествиям не представлялось бы никакой возможности.

Итак, предмет, которым строится пространство, не должен обладать в полной мере зрительной осью, то есть его ось не должна превращаться в зрительный центр, но, с другой стороны, предмет без своего основного стержня, не имеющий своего предметного центра, тоже не был бы пригоден для этой цели; ставя его в различные повороты и положения, мы не могли бы ясно представлять как отдельного его положения, таки, с другой стороны, относительности положения предмета к предмету.

Как я уже говорил и обращаю внимание еще раз, таким предметом по преимуществу будет человек, так как он есть объем, имеющий вертикальную ось. Вертикальность оси объема имеет для нас значение принципиальное, так как типичное восприятие объема будет горизонтальным путешествием вокруг вертикальной оси — будет это практически или мысленно.

В изображении человека такое принципиальное положение объемной оси сливается с функциональным положением человека, с положением стояния, но поэтому-то всякий наклон этой оси в том либо другом направлении будет всегда очень остро восприниматься и требовать определенного обоснования.

Но, во всяком случае, изображение, имеющее определенную объемную ось, будет очень пригодно для действия им как единицей, так как мы сможем его двигать и сможем точно так же устанавливать ясные и простые отношения между этими единицами.

Типичное положение объемного изображения человека прежде всего дает параллельность всех осей объемов, и кроме того, если мы возьмем землю как .горизонтальную поверхность, то мы будем иметь не только параллельность объемов, но и все их соответствующие друг другу части на одинаковой высоте.

Это явление мы встречаем особенно остро выраженным в раннем Ренессансе (хотя бы у Мазаччо), оно носит название изокефалии. Почти всегда его пытаются объяснить натуралистическими мотивами, но это едва ли верно, так как при взгляде на подобную картину мы поражаемся нарочитостью и ненатуральностью, и такой прием находит себе настоящую и действительную цену в том, что нам при этом становится нагляднее аналогия между отдельными фигурами, мы легко соотносим головы к головам, торсы к торсам и так далее.

Так вот, при наличии параллельности осей и при возможной подобности по высоте, мы легко можем себе представить, как строится изобразительная поверхность. Это будет как бы забор из фигур, каждое бревно которого будет аналогично обработано и на одинаковой высоте будет иметь одинаковые части.

Этот факт, кроме того, что дает построить легко и просто воспринимаемую поверхность, наталкивает, естественно, на то, чтобы эти объемы обменивались своими качествами, наталкивает на то, чтобы, если что не может сказать один — за него говорил бы другой, и обратно; словом, параллельность объемов дает возможность аналогизировать их и придавать положения и качества всех других какому-либо одному.

Но тут надо заметить, что качества человеческой фигуры — то, что она имеет лицо и спину, то, что у нее есть фас и профиль, то есть что при вращении объемной оси она поворачивается к нам качественно различными сторонами, играет решающую роль.

Нам оказывается чрезвычайно важным, что ее повороты относительно нас не безразличны, а имеют качества, следовательно, имеют и какие-то твердо воспринимаемые положения в этих поворотах; так как иначе, если бы мы имели только токарные объемы, то их поверхности очень бы сильно выражали движение вокруг объемной оси, но тем самым, что всякое положение не отличалось бы от другого, мы хотя и ощущали бы его, но без возможности дать себе ясный отчет.

Первым простейшим примером может быть такой: если мы рядом изобразим человека с лица и со спины, имея параллельные оси, эти два изображения будут аналогизироваться, отождествляться нами, они ведь, кроме того, будут иметь совершенно одинаковый контур, что тоже будет способствовать отождествлению.

Тогда получится то, что мы будем налагать одно на другое, качества одного и другого прикреплять к одной из двух осей, тогда получится, •что мы в одном предмете будем иметь изображенным и лицо и спину.

Надо думать, что чистые повороты лица и спины будут, правда, налагаться друг на друга, но слабо будут мыслиться как моменты движения одного и того же предмета; и поэтому, удовлетворяя такому наложению, но в то же время являясь более неустойчивыми и поэтому расположенными к движению, полуобороты лица и спины дадут еще более яркое выражение тому, о чем здесь говорится.
Разбираясь дальше в качествах человеческой фигуры, мы наблюдаем, что почти при всяких поворотах она имеет довольно ярко выраженную основную ось, поэтому мы и можем мыслить каждый поворот как момент вращения; но существуют два поворота человеческой фигуры, которые привносят с собой нечто новое, каждый в своем роде, и поэтому мыслятся особо, как бы являются большими остановками в поворотах объема: это человеческий фас и профиль. Тот и другой может более или менее сохранить объемную ось, но каждый из них получит особые качества.

Фас будет исключительным выражением объема, будет прикреплен к изобразительной поверхности только своей осью; контур же будет отлипать от изобразительной поверхности; профиль же будет, так сказать, несколько стелиться по поверхности и двигаться по ней.

Фас будет вещь сама по себе и может стать основой лица вещи, но будет нарушать поверхность; профиль будет вещь функциональная, вещь в движении, будет утверждать поверхность, но безграничную.

Что же получится, если мы так же, как спину и лицо, соединим фас и профиль, причем для этого соединения мы должны в профиле все-таки оставить некоторый намек на объемную ось.

Тогда мы наложим качества одного на качества другого, к одной объемной оси прикрепим обе формы, и в результате окажется, что фас тем самым приобретет качества профиля, то есть плоскостность, и перестанет нарушать изобразительную поверхность, а профиль приобретет качества фаса, то есть получит прикрепление к месту, и тем самым хотя и не потеряет плоскостности, но уже не будет нарушать границ плоскости, не будет иметь тенденцию за них выскочить.

Таким образом, приняв во внимание качества человеческих поворотов и орудуя ими, мы при помощи объемной оси объединяем их и тем самым даем плоскостное выражение объему (профиль служит как бы поплавком, чтобы фас не тонул своими контурами в изобразительной поверхности); с другой стороны — утверждаем при помощи фасовой остановки и при помощи профильного движения плоскость, как ничем другим.

Отчасти такое же значение, то есть утверждение изобразительной плоскости, будет тогда, когда мы поставим оси объемов под каким-либо углом; их угловое отношение будет утверждать плоскость.

Но вообще надо сказать, что близость двух объемов, почти слияние или даже соприкасание их будет всегда вести к тому, что объемы как бы выпьют друг друга и в конце концов мы потеряем и тот и другой.

Этого совершенно не будет, если мы будем сближать профиль и фас, так как профиль, будучи плоскостью, даже рассекши объем, не нарушит, не выпьет его.

Из этого следует, что даже ближайшее соседство профиля и фаса не нарушит объема, а выполнит только с большей силой то, о чем здесь ранее говорилось.

Отсюда может возникнуть вопрос: в отдельной человеческой фигуре не должно ли соседствовать одно рядом с другим — формы фасные, имеющие ось вращения, и формы профильные, утверждающие плоскостность соседних фасных. И действительно, мы можем припомнить несколько примеров, указывающих на то, что объем, плотно прикасаясь к объему, нарушит его. Как раз во избежание этого скульптурные звери из бронзы, как китайские, так и персидские, имеют очень полное туловище, которое и изображает собой основной объем, а второстепенные объемы, как-то: шеи или ноги, до того утоныпаются, что уже не воспринимаются как объем, а как одномерность. То же самое мы можем наблюдать и в персидских миниатюрах, когда изображается лошадь: туловище тоже превалирует, а нога приближается к одномерности.

То же самое будет справедливо и относительно соединения фасных и профильных форм на плоскости, только еще с тем плюсом, что фас становится плоскостным, то есть мы получаем плоскостное изображение объема.
Но в таком соединении фаса и профиля, которое само по себе есть орудование над предметом для построения пространства, получает свое основание широкое развитие симметрии, которое без этого не получилось бы и не приобрело бы нового смысла.

Ведь если мы имеем только более или менее симметричного контура объемы, то в симметричное положение они могут встать только по своим осям.

Вообще понятно, что на всем протяжении Ренессанса мы видим, что в том либо другом смысле, а работают с симметрией. Симметрия понимается как отношение предметов, а так как искусство в большей мере исходит в это время от предмета, то естественно, что всякое их отношение друг к другу играет важную роль. Поэтому и симметрия приобретает сильное значение, [она] получает отчасти новый смысл, сравнительно с египетской, но во многом аналогична греческой фронтонной симметрии.

Но вернемся к предыдущему.

При простых объемах, имеющих объемные оси, при симметрично-контурных (более или менее) изображениях может быть симметрия только положений, которую мы будем учитывать как симметрию осей.

Симметричны будут наклоны этих осей. Такую симметрию мы наблюдаем у Гирландайо и у Рафаэля, и такая симметрия имеет сказать нечто новое; так, если бы она была только двухмерной, то она была бы очень скудна, и поэтому естественно, что она пользуется трехмерностью и либо валит на нас, либо валит от нас оси объемов, следовательно, завоевывает для симметрии новую область.

Но как-никак богатство симметрии дается ей профилем: когда мы имеем профиль, то имеем и богатство образов симметрии.

И в этом смысле древняя симметрия, хотя бы египетская, основывается исключительно на профиле, и поэтому она есть симметрия в двух измерениях; кроме того, она по большей части простая симметрия, то есть имеющая одну ось вертикальную, поворотом вокруг которой и давалась симметричная часть рисунка.

Когда же в итальянском искусстве мы видим работу над типичным объемом, то естественно, что в этом направлении возникает симметрия положения осей, и этим самым она переносит свои законы и на трехмерное. Но тем не менее относительно двухмерного она будет скудной и не очень выразительной.

Дело совершенно меняется тем, что наряду с более или менее фасными образами входит профиль, он несомненно вносит оживление; но особенно обогащаются опыты в этом отношении, когда мы в одном изображении отдельного предмета определим некоторые части как фасные, а некоторые — как профильного значения.

Подобное мы видим, конечно, у многих, но особенно выразительно это у Тинторетто, там почти каждая фигура являет своим торсом некоторую фасную форму, а конечности трактуются как профильные, причем они даже располагаются по большей части с одной стороны, иногда даже кажется, что, собственно, только одна нога и одна рука берутся как необходимые, а другие рисуются только из приличия.

Но, во всяком случае, возможность в одной фигуре соединить и фасность, и профильность позволяет такой симметрии воспользоваться богатством и плоскостных двухмерных и трехмерных отношений, так как здесь мы можем работать над симметрией положения осей, а также и над профильной симметрией, что в общем дает неисчерпаемое богатство.

Профильной симметрией пользуется уже Мазаччо, но там профиль берется отдельно; постепенно развиваясь, у Тинторетто профильность и фасность соединяются в одном предмете и в конце концов доходят в угоду симметрии до того, что фигура человеческая уподобляется волюте с внутрь повернутыми или контрастно поставленными ветками, какую мы и встречаем потом, во время барокко, в большом употреблении.

И правда, если мы попытаемся чертить симметрично поставленные линейные формы, то мы невольно начертим подобную волюту ,в которой еще можно усмотреть фасную объемную ось, а профильные дуги сами собой бросаются в глаза.

Но, выяснив, что для богатства форм симметрии необходимо было, чтобы в одном предмете объединились бы фасность и профильность, мы должны обратиться к рассмотрению вопроса: почему важна симметрия, какое она вообще имеет значение.

Смысл египетской симметрии в том, что она создает новый профильный организм, как бы порождает новое двухголовое чудовище, которое имеет некоторые преимущества на двухмерной безграничной пустыне двигательной изобразительной поверхности; оно двигается в обе стороны, и в этом преимущество [подобной формы]. С другой же стороны, она прикреплена к вертикальной оси и тем самым закрепляет за собой как бы для памяти некоторое место поверхности, которым этот организм безусловно владеет.

Здесь мы по большей части имеем дело с одним организмом, и отпустить части этого организма далеко от оси симметрии боятся, так как тогда влияние этой оси перестанет давать себя знать и симметрия нарушится. Но постепенно эти части все-таки отделяются, опредмечиваются, и тогда уже дело идет не об одном симметричном организме, а о двух или нескольких предметах, по форме одинаковых, но находящихся в разных пространственных положениях, но так, что, взяв один предмет, мы можем проделать с ним некоторые эволюции ,в конце которых этот предмет належится и совпадет с тем, который ему симметричен.

Следовательно, в древней симметрии дело идет об одном симметричном организме, тогда как позднее — вопрос, собственно, о восприятии подобия предметов на основании оси симметрии.

Отсюда следует, естественно, что симметричные предметы могут более или менее удаляться от оси симметрии и могут путешествовать вверх и вниз по оси и этим ясность их подобия не теряется. Нам существенно это последнее, так как древнюю симметрию мы должны, собственно, воспринимать как бы обеими руками в обе стороны, а симметрию позднюю мы берем, воспринимая в одном предмете через подобие, которое нам подтверждается осью симметрии: другой [предмет] мы как будто и не принимаем во внимание, смотрим на него боковым зрением.



Словом, в таком смысле симметрия есть изображение движения[одного] предмета по пространству [другого] предмета, подобного фигурой, что позволяет рассматривать предметы как отдельные фазы этого движения; а оси симметрии дают некоторые точки композиции, которые владеют сразу многими точками различных предметов и соединяют их; и мы можем думать, что, беря один предмет, мы в то же время берем все ему подобные и симметричные.

Словом, симметрия есть средство связать подобием два предмета таких, которые как будто по внешности и не подобны; кроме того, так как ключом к их подобию является ось симметрии, которая указывает необходимое для удостоверения в подобии движение, то и это движение бессознательно входит в наше восприятие и тем самым порождает в нас более или менее ясные представления о промежуточных моментах движения предмета.



Но мы пока говорили только о симметрии, ключом к которой является ось; но можно себе представить такую [симметрию], ключом к которой будет точка; это получится, если мы один из симметричных предметов обернем вокруг горизонтальной оси, так сказать, вверх ногами. Таким образом, мы как будто получим симметрию более отдаленную, так как все больше и больше эволюции нужно проделать с одним предметом, чтобы он совпал с другим.

Но оказывается, что ключом к этой симметрии в более узком смысле будет уже не ось, а точка, так как у нас имеются две оси: вертикальная и горизонтальная, перекрещивающиеся друг с другом и в самом перекрестии имеющие одну общую точку, которая этими осями владеет.

Кроме того, чувственность этой формы симметрии, как это ни странно, гораздо сильнее, то есть, несмотря на то что [имеется] несколько осей и эволюции сложнее, [тем не менее] мы как бы нагляднее воспринимаем подобие предметов.

Объясняется это тем, что если мы попробуем все подобные точки предметов соединить прямыми линиями, то линии эти пройдут через точку симметрии. Таким образом, точка симметрии владеет всеми точками [обоих] предметов как того, так и другого.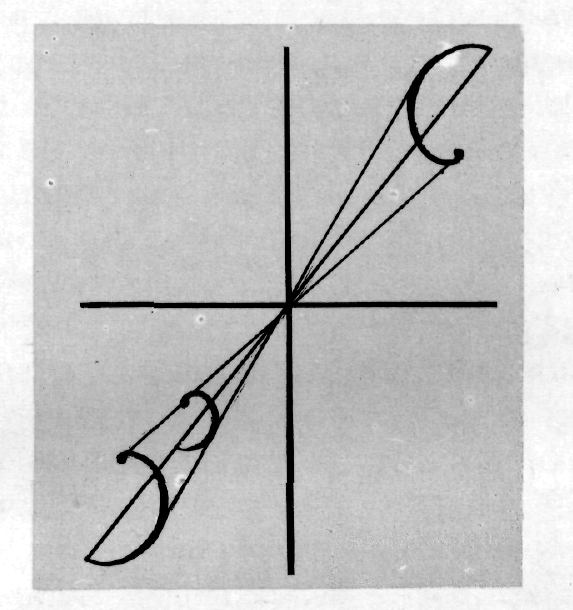



Это с одной стороны, с другой же — действует еще и то, что при та-кой симметрии, фигуры не только подобны, но и каждая их часть параллельна соответственной части другого предмета. В данном случае параллельность действует особенно удивительно, так как мы ее чувствуем, но совершенно ей не верим и нам нужна проверка, чтобы убедиться в этом.

Кроме того, подобие, соответствие, зависимость предмета от предмета усугубляется тем, что части, параллельные соответственным другим, необходимо перпендикулярны, то есть тоже и с ними стоят в определенной связи и указывают на них.

Естественно, что в такой симметрии отдаление предметов от осей симметрии может иметь место в полной мере, так как, собственно, каждая линия, соединяющая подобные точки, раз она проходит не-обходимо через точку симметрии, тем самым становится точно такой же равноправной осью симметрии.

Словам, в такой симметрии осей симметрии будет бесчисленное множество, бесконечное число, и, кроме того, они возбудят еще в нас представления о новых поворотах предметов, тоже бесчисленное количество, словом, сколько осей, столько и новых, еще не нарисованных поворотов, но которые могут до известной степени чувствоваться.

И если бы мы все это нарисовали, то получился бы такой водоворот, что у нас закружилась бы голова.

Вот в этом-то обнаруживается некоторый, так сказать, дурной характер симметрии, о котором мы поговорим в конце. Сейчас же пойдем дальше.

Благодаря точке симметрии, между прочим, могут быть симметричными предметы подобные, но разной величины, так как все подобные в них точки могут быть соединены прямыми, которые пройдут через точку симметрии.

Отсюда можно объяснить излюбленную форму волюты, употреблявшуюся в Ренессансе и главным образом в барокко. Вообще волюта с двумя противоположно загнутыми концами есть форма двуосной симметрии, ключом к которой является точка. Но в барокко употребляется волюта с разной величины завитками: один — маленький, другой — большой, и это понятно, так как при точечной симметрии возможна симметрия предметов разных величин.

Чтобы яснее стала власть осей симметрии и власть точки симметрии, мы должны вспомнить из нашего рассмотрения греческих рельефов то, какую там композиционную роль играли прямые линии и точки пересечения этих прямых. Всякая прямая, не только вертикаль, есть в противоположность кривой более статичная линия; она, конечно, может [быть] воспринята как движение, но может также, и последнее скорей, [быть] воспринята как остановка; отсюда следует, что тогда мы ее воспримем сразу более или менее одновременно. Таким образом все, что на нее попадет, объединяется ею, становится одновременнее.

Когда же линии пересекаются, то, будучи в точке пересечения, мы владеем как бы и той и другой линией; мы как бы присутствуем сразу во всех точках той и другой; мы во всяком случае близки к этому.

Вот такой властью обладают оси симметрии, и такой же властью обладает точка симметрии, а через нее некоторую власть приобретает и каждая точка предмета.

Но что касается точки симметрии, то ее власть уже превосходит всякие границы, так как так много ей подвластно, что в конце концов эта власть теряет свое значение, становится чем-то вредным в изобразительном искусстве.

Получается такое колесо, которое дьявол у Анатоля Франса показал монаху, чтобы убедить его, что истина белая, то есть никакая. Так получается и тут. Поэтому-то в симметрии и коренятся некоторые дурные качества.

Ведь, как мы видели, подобие предметов, позволяющее как бы через один воспринять другой или другие, имеет смысл в том, что в незавоеванную область пространства посылается предмет, который по подобию как бы возвращается обратно к первому, таща за собой покоренную область. Вот здоровый смысл симметрии. Но, как видите, если ей дать волю, то получится не подчинение одному многого, а бесконечное путешествие от подобия к подобию, и так без надежды когда-либо кончить.

Царем остается только точка симметрии, но вы из лекции Флоренского знаете, что точки бывают разные и есть из них очень опасные, какова, например, точка перспективного схода. По-видимому, в крайнем своем развитии и точка симметрии близка ей по характеру.

Во всяком случае, когда все течет и изменяется, переходит одно в другое, одна точка только стоит, то тут нет ничего хорошего, так как пространство не получает, таким образом, единства и ясности, а беспредельную в дурном смысле многообразность (или однообразность!).