Роберт Вильгельм Бунзен
 Скачать 2.24 Mb. Скачать 2.24 Mb.
|
|
Раздел химической термодинамики, который изучает тепловые эффекты химических реакций и фазовых переходов, называется термохимией. Обычно химические реакции проводят при V = const или Р = const. Если V = const, то Qv = ∆Uv, если Р = const, то Qp = ∆Up – p∆V, таким образом, при V или Р = const теплота процесса приобретает свойства функции состояния, т.е. не зависит от пути процесса. Qp и Qv называют изобарным и изохорным тепловыми эффектами реакций. Независимость теплового эффекта процесса от пути его протекания была установлена опытным путем русским ученым Г.И. Гессом в 1836 г. Тепловой эффект процесса не зависит от промежуточных стадий, а определяется начальным и конечным состояниями системы. Математическое выражение закона Гесса: Qv = ∆U; Ор = ∆Н Представим себе процесс превращения исходных веществ в продукты реакции различными путями: 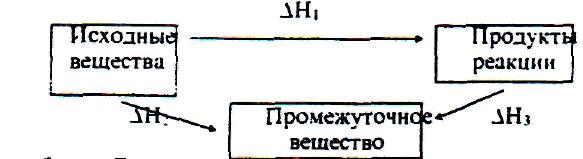 Закон Гесса утверждает, что указанные тепловые эффекты связаны между собой соотношением ∆H1 = ∆H2 + ∆H3 В термохимии используют термохимические уравнения реакций. Термохимическими называют такие уравнения, в которых приведены тепловые эффекты. Тепловой эффект реакции зависит от природы реагирующих веществ и их агрегатных состояний, поэтому а термохимических уравнениях символами (г. ж. т) обозначают состояния веществ. Например, H2(г) + ½О2(г) = Н2О(ж) – 284,2 кДж/моль Применяя закон Гесса. можно определять тепловые эффекты реакций, которые экспериментально определить нельзя. Рассмотрим пример определения теплоты гидратообразования сульфата меди (II) CuSО45H2О CuSО4 + 5H2О = CuSО45H2O. Теплотой гидратообразования называют теплоту, выделяемую при присоединении к 1 моль твердой безводной соли кристаллизационной воды до образования устойчивого кристаллогидрата. Экспериментальное определение теплоты образования CuSO45Н2О затруднительно, т.к. одновременно образуются кристаллогидраты различного состава. (∆Hm)1 CuSO4 Cu2+SO42- (раствор) (∆Hm)3 (∆Нm)2 CuSO45H2O Гидратированные ионы Cu2+ и SO42- можно получить двумя путями: 1) растворением CuSO4 и 2) растворением CuSO4 через образование кристаллогидрата. Исходя из закона Гесса: (∆Нm)1 = (∆Нm)2 + (∆Нm)3 где (∆Нm)1, (∆Нm)2, (∆Нm)З – соответственно интегральные теплоты растворения CuSO4, CuSO45Н2О и теплота гидратообразования. Тогда теплота гидратообразования: (∆Нm)3 = (∆Нm)1 – (∆Нm)2 Интегральной теплотой растворения (∆Нm) называют изменение энтальпии при растворении 1 моль вещества в некотором количестве чистого растворителя. Закон Гесса позволяет также определять теплоты нейтрализации сильных кислот и сильных оснований. Теплотой нейтрализации называют тепловой эффект реакции образования 1 моль жидкой воды из ионов водорода и гидроксила: Н+ + ОН- = Н2О + Q1 Для того, чтобы можно было сопоставлять тепловые эффекты различных реакций и проводить термохимические расчеты, введено понятие теплового эффекта при стандартных условиях. Под стандартным тепловым эффектом понимают его величину при давлении 1.01.105Па и температуре ТºК. В настоящее время термохимические исследования чаше всего проводят при 25°С. В справочных таблицах тепловые эффекты приводят при Т = 298ºК и записывают стандартный тепловой эффект – ∆Н°298. Из закона Гесса вытекает несколько следствий, два из которых применяются для расчета тепловых эффектов: 1). Тепловой эффект реакции равен алгебраической сумме теплот образования продуктов реакции минус сумма теплот образования исходных веществ с учетом стехиометрических коэффициентов: ∆Н°298 = Σvi∆Н°298 (прод) – Σvi∆H°(исх) Теплотой образования называют то количество теплоты, которое выделяется или поглощается при образовании 1 моль вещества из простых веществ, взятых в устойчивом состоянии при рассматриваемых условиях (р,Т). 2). Тепловой эффект реакции равен алгебраической сумме теплот сгорания исходных веществ минус сумма теплот сгорания продуктов реакции с учетом стехиометрических коэффициентов. ∆Н298 = Σvi∆Hc298(исх) – Σvi∆Hc298(прод) Теплота сгорания – количество теплоты, которое выделяется при полном сгорании 1 моль вещества до высших оксидов при данных условиях (р, Т). ТЕПЛОЕМКОСТЬ Средней теплоемкостью называется количество теплоты Q, поглощаемое при нагревании 1г или 1 моль вещества на t: С = Q / ∆Т Истинной теплоемкостью называют отношение бесконечно малого количества теплоты δQ. полученного телом, к соответствующему изменению его температуры: C = δQ / dT Процесс нагревания или охлаждения чаше проводят либо при Р = const, либо при V = const, тогда Cv = δQv / dT; Cp = δQp / dT Теплоемкости Ср и Cv отличаются на величину работы, необходимой для изменения объема системы: Ср – Cv = R Теплоемкости твердых, жидких и газообразных веществ повышаются с температурой: Ср = f / (Т). Однако эту зависимость нельзя определить на основании законов термодинамики, она изучается экспериментально. Обычно для расчетов применяется уравнение Ср = а + вТ + с'Т-2 +..., где а, в и с' – постоянные, которые для многих веществ могут быть найдены в справочнике. Согласно закону Гесса можно вычислить тепловой эффект реакции при той температуре (обычно 298), при которой известны теплоты образования всех реагентов. Однако часто необходимо знать тепловой эффект реакции при различных температурах. Уравнение, дающее зависимость ∆Н от Т называется уравнением Кирхгоффа (интегральная форма): 298ʃT ∆H°T = 298ʃT ∆CpdT ∆H°Т = ∆H°298 + 298ʃT (∆а + ∆bТ + ∆сТ2 + ...) dT ∆Н° = ∆Н°298 + ∆а (Т – 298) + ∆b/2 (Т² – 2982) – ∆с' (1/Т – 1/298) Расчеты тепловых эффектов реакции по уравнению Кирхгофа производят при составлении тепловых балансов процессов производства различных химических веществ, в том числе и лекарственных соединений. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ Используя первый закон термодинамики нельзя определить направление течения самопроизвольного процесса при данных условиях. Решить этот вопрос можно с помощью 2-го закона термодинамики. Первооткрывателем 2-го закона считается С.Карно, который изучал теплоты в работу в тепловых машинах. Карно установил, что теплота, полученная от нагревателя (Q1) не может полностью переходить в работу, часть её (Q2) передаётся холодильнику.
КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ 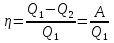 Некоторые формулировки 2-го закона
η= (T1-T2)/T1
Математическое выражение 2-го закона термодинамики для любого произвольного процесса dS > (δQ)/T В том случае, когда отсутствуют теплообмен между системой и окружающей средой (SQ >= 0), т.е. система изолирована. dS>0 Таким образом, если система изолирована, при протекании в ней обратимых процессов энтропия не изменяется, при необратимых процессах она растёт, т.е. энтропия является критерием самопроизвольных процессов в изолированных системах. Увеличение энтропии связанно с усилением хаотического движения молекул, т.е. рост энтропии связан с увеличением неупорядоченности в системах, т.е. энтропия - мера беспорядка. ИЗМЕНЕНИЕ ЭНТРОПИИ ПРИ РАЗЛИЧНЫХ ПРОЦЕССАХ
dS = δQ/T; δQ =L (теплота фазового перехода)
ΔS = ∫δQ/T =0
δQp=CpdT; δQp=TdS; CpdT=TdS dS=CpdT/T; ΔS = ∫CpdT/T = Cp lnT2/T1.
ΔS=CvlnT2/T1. ПАСТУЛАТ ПЛАНКА Планк выдвинул пастулат: Энтропия любого индивидуального бездефектного кристаллического вещества при абсолютном нуле равна 0. S0=0 В соответствии с этим постулатом для идеального твёрдого тела энтропия равна: S = ∫Cp/TdT, а для вычисления энтропии газа при некоторой Т: S =∫Ср(т)/ T dT + Lпл/Тпл + ∫Ср(ж)/Т dT + Lисп/Тисп + ∫Ср(г)/Т dT Lпл, Lисп теплоты фазовых переходов при плавлении и испарении. ТЕРМОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ Энтропия определяет возможность протекания самопроизвольного процесса в изолированной системе. Для закрытых систем также имеются функции, знак изменения которых позволяет судить о направлении самопроизвольного процесса, такие функции называются характеристическими, а соответствующие каждой из этих функций пара постоянных параметров называются естественными переменными. Наиболее широко в термодинамике используются 5 характеристических функций: Первые четыре термодинамические потенциалы. Термодинамическими потенциалами называются функции, которые характеризуют способность системы совершать работу. СООТНОШЕНИЕ МЕЖДУ ТЕРМОДИНАМИЧЕСКИМИ ПОТЕНЦИАЛАМИ В обычных условиях для определения направления самопроизвольного процесса чаще используется изменение энергии Гиббса (изобарно-изотермический потенциал) ΔG = ΔН-Т ΔS | (Уравнение Гиббса-Гельмгольца). Исходя из этого уравнения, можно показать, что самопроизвольный процесс при р,Т= const возможен, если ΔG < 0, т.е. эта функция является критерием направления самопроизвольного процесса. Используя уравнение Гиббса - Гельмгольца, уравнение Кирхгофа и постулат Планка, можно получить объединённое уравнение для расчёта ΔGT. Для решения уравнения используются 3 степени приближения:
т.е. ΔСр=0, тогда ΔGt = ΔН298 -Т ΔS298
при Т=298К ΔСр = Δа=const; ΔСр=ſ(Т)-неизвестна ΔGt = ∆Н298-Т ΔS298+ Δа(Т-298) - Δа Т ln (Т/298)
ЗАКОН ДЕЙСТВУЮЩИХ МАСС Все химические реакции протекают одновременно в двух направлениях: в сторону образования продуктов реакции (прямая реакция) и в сторону превращения продуктов в исходные вещества (обратная реакция). Вследствие химической обратимости реакции не доходят до конца, а доходят до состояния химического равновесия, которое характеризуется постоянством равновесных концентраций (или парциальных давлений) всех участников реакции при постоянстве внешних условий и минимальном значении энергии Гиббса или энергии Гельмгольца. В 1867г. математиком Гульдбергом и химиком Вааге был сформулирован закон действующих масс, который показывает связь между равновесными концентрациями веществ, участвующих в химической реакции. Для реакции: аА+bВ ⇄ qQ +rR Кс = (Сq * Сr) / (Сa* Сb), Кр = (Рq*Рr) / (Рa * Рb) Отношение произведения равновесных концентраций (порциальных давлений) продуктов реакции, взятых в степенях, равных их стехиометрическим коэффициентам, к такомуже произведению концентрации исходных веществ при данной температуре есть величина постоянная, называемая константой химического равновесия. Константы равновесия зависят от природы реагирующих веществ, температуры не зависят от концентрации. В случае гетерогенных реакций в выражение константы химического равновесия входят парциальные давления (или концентрации) только газообразных участников реакции, например для реакции: СаСО3 гв ⇄ СаОгн +СО2(г) : Кp = PСО2 Константа равновесия связанна с энергией Гиббса и Гельмгольца уравнениями изотермы химической реакции: ΔGт = RT(ln(Рq*Рг) / (Pa * Рb )-In Кр), Р1 Т =const Р1 - парциальные давления веществ в исходном состоянии. ΔFт= RT((Сq * Сr )/( Сa* Сb)-ln Кс) Различные химические реакции можно сопоставить по их способности к самопроизвольному протеканию. Такое сопоставление принято проводить для условий, когда все вещества, участвующие в реакции, находятся в стандартных состояниях, т.е. когда активности каждого из них равны 1 или парциальное давление каждого компонента равно 1 атм.((Рq ) *( Рг)) / (Pa * Рb =1), тогда ΔGт0 = -RTlnKp; ΔFт0 = -RTInKc. ВОПРОСЫ ПО ТЕМЕ: "ТЕРМОДИНАМИКА"
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ Задача 1 Определить тепловой эффект химической реакции в стандартных условиях среды при 500 К: СНз ОН + 3/202(г) = СО2(г) + 2 Н2 0(г) Решение. Из справочника (5) выпишем необходимые для расчета термодинамические величины
Для расчёта теплового эффекта и изменения теплоёмкости применим следствие из закона Гесса, при этом учитываем, что для простых веществ стандартная теплота образования равна нулю. ΔНР ΣΔНſкон - ΣΔНſисх= ΔНР(СО2)+2ΔН(Н20) - ΔН(СНзОН)=(-393,51)+ + 2(-241,84) - (201,2)= = -675,99 кДж. Знак минус перед тепловым эффектом означает, что теплота выделяется в результате реакции. ΔСр298 = Ср (СО2) +2Ср (Н20) - Ср(СНзОН) - Ср (О2) = = 37,13+2*33,56 - 43,9 - 3/2 *29,36 =16,31 Дж/К Тепловой эффект при 500К находим по уравнению Кирхгофа, где принимаем Ср = Ср298 = const. ΔН500=ΔН298 + 298∫500 ΔСр dT= -675,99*103 + 16,31(500-298)=672,70*103 кДж= = - 672,7 кДж |
