Шпоры по матану(1 курс). 1. Функция, одз

• Название: 1. Функция, одз
• Анкор: Шпоры по матану(1 курс).doc
• Дата: 25.03.2018
• Размер: 0.69 Mb.
• Имя файла: Шпоры по матану(1 курс).doc
• Тип: Документы; #17195
• страница: 18 из 33

12. Выпуклые функции в Rⁿ и их свойства.

Отрезок в Rⁿ с концами a, b  Rⁿ – это множество точек

х (t)= (1-t) a + t b,

где t произвольное число из промежутка 0; 1. Отрезок с концами a, b обозначается  a, b . Отрезок  a, b  совпадает с множеством точек в Rⁿ, представимых в виде с = а + b , где , - произвольные неотрицательные числа такие, что . Множество Р  Rⁿ называется выпуклым, если вместе с любыми двумя точками a, bР оно содержит и весь отрезок  a, b . Функция n переменных f (х), определенная на выпуклом множестве РRⁿ , называется выпуклой, если для любых двух точек a, b  Р и любых двух чисел ,0; 1 таких, что , выполняется неравенство

f (а + b) ≤  f (а) +  f (b)

Для непрерывной функции, заданной на выпуклом множестве Р , следующие условия равносильны:

1. 
   f выпукла;
   

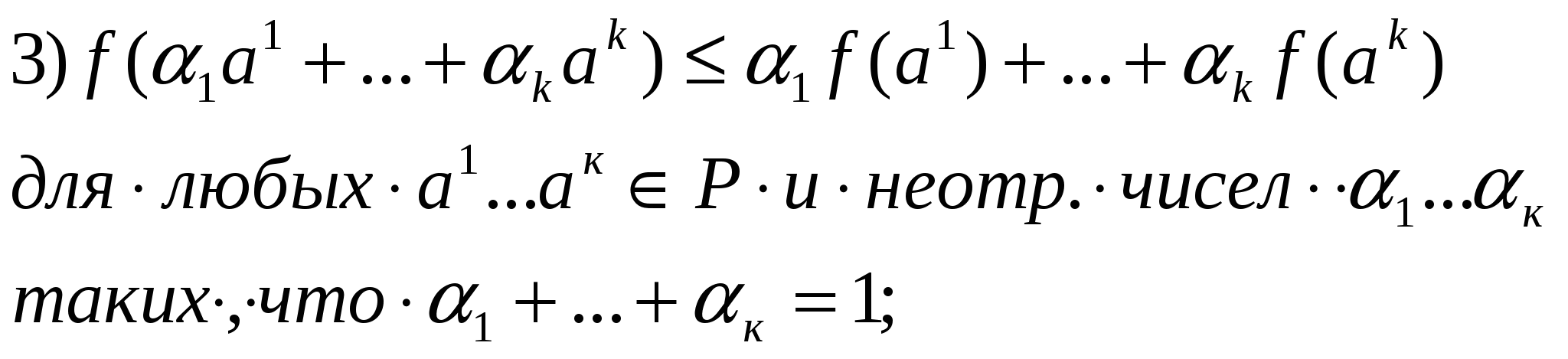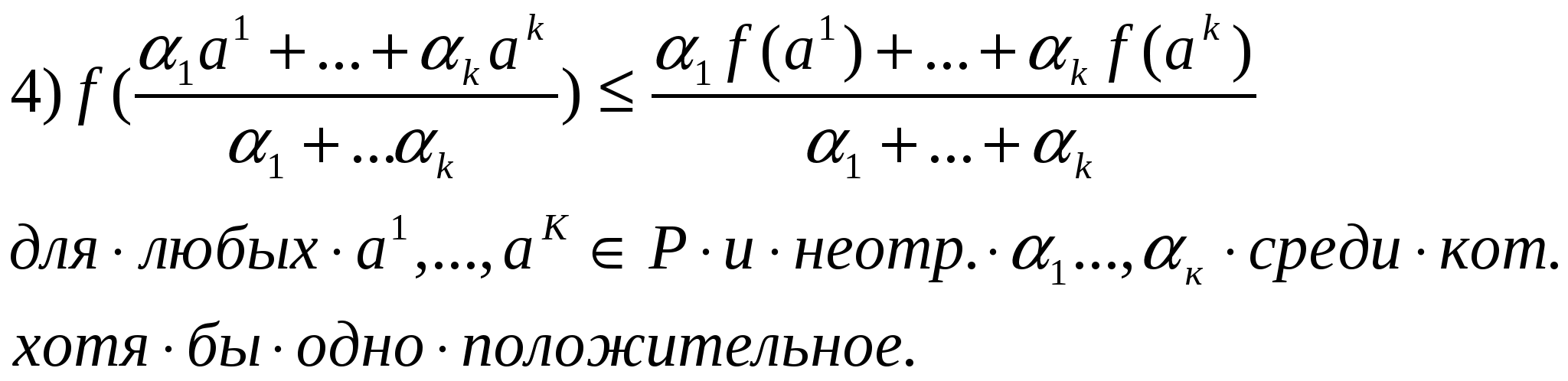Неравенство из пункта 4 называется неравенством Йесена. выпуклая функция наз. строго выпуклой, если неравенство f (а + b) ≤  f (а) +  f (b) строгое при всех a, b из области определения функции и α,β ≥0 таких, что α+β=1.

Функция f наз. (строго) вогнутой, если –f (строго) выпукла, т.е.

f (а + b) ≥  f (а) +  f (b)

Линейная функция f(x)=(c,x)+c₀ одновременно выпукла и вогнута, но не строго.

Свойства выпуклых функций.

1. 
   функция с выпуклой областью определения Р  Rⁿ выпукла тогда и только тогда, когда выпукло множество Н_f ={(х,у):хР, у≥f(x)} (из Rⁿ⁺¹) называемое надграфиком функции f(x).
   
2. 
   Если f(x) выпукла, то функция αf(x) выпукла при α>0 и вогнута при α<0.
   
3. 
   Если f(x) выпукла на Р, то множество U_f (α)={х:f(x) ≤α} выпукло при любом α. (обратное утверждение неверно).
   
4. 
   Сумма любого числа выпуклых функций на множестве Р  Rⁿ выпуклана Р , если при этом хотя бы одна из суммируемых функций строго выпукла, то вся сумма строго выпукла.
   
5. 
   Пусть Р  Rⁿ – выпуклое множество, и для каждого i=1,2,…k пусть l_i(x) – линейная функция n переменных , а f_i(t) – функция одной переменной , выпуклая на l_i(Р). Тогда функция F(х)=f₁ (l₁(x))+…+ f_К (l_К(x)) выпукла на Р. При этом, если все функции f_i(t) строго выпуклы и любая точка однозначно определяется набором (l₁(а)+…+ l_К(а)), то F(х) строго выпукла.
   
6. 
   Пусть f выпукла на Р  Rⁿ , а φ(t) – возрастающая выпуклая функция на множестве f(Р) R, тогда F(х)= φ(f(x)) выпукла на Р. Если f(x) строго выпукла, то и F(х) строго выпукла.
   
7. 
   Дифференциируемая функция f(x) выпукла на множестве Р  Rⁿ тогда и только тогда, когда (grad f(a), b-a) ≤f(b)-f(a) для любых a,bР
   
8. 
   Пусть f(x) – функция, непрерывная на отрезке  a, b R и дважды дифференциируемая на (a, b). Для выпуклости функции f(x) на  a, b  необходимо и достаточно выполнение неравенства f˝(x)≥0 для всех t (a, b). Для строгой выпуклости f(x) добавляется условие f˝(x)≠0 ни на одном интервале, содержащемся в (a, b).
   
9. 
   Пусть D – выпуклое открытое множество в пространстве Rⁿ, f(x)=f(x₁,…,х_n) – функция, имеющая в D непрерывные частные производные второго порядка. Для каждой точки х D положим
   

и составим матрицу

C=Cij(X). Функция f(x) строго выпукла на множестве D , если в каждой точке х D выполняются следующие неравенства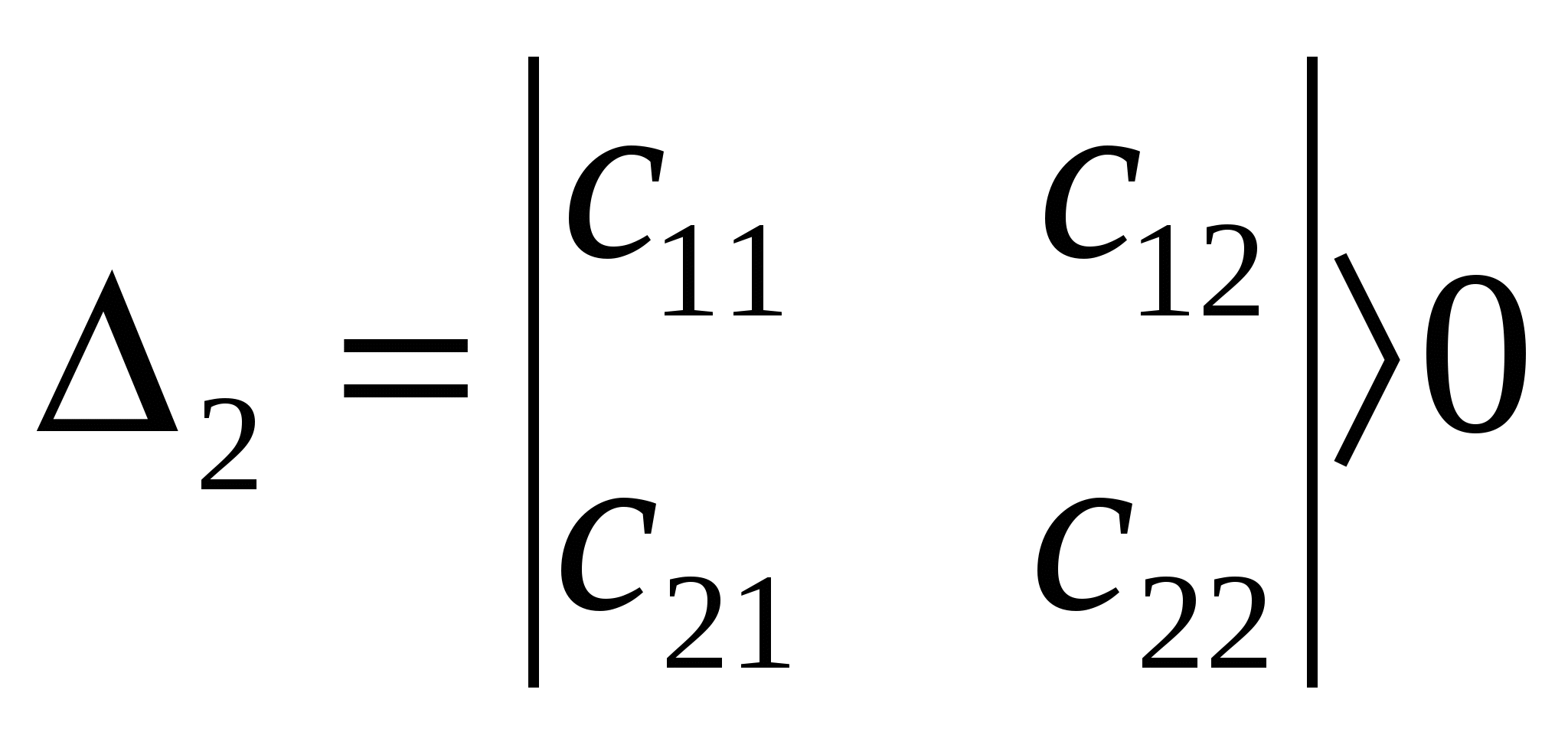

∆
₁=с₁₁>0, …, ∆_n=det c>0

Экстремальные значения выпуклых и вогнутых функций.

1.Если х* - точка локального минимума (максимума) выпуклой (вогнутой) функции f(x) на выпуклом множестве Р  Rⁿ то f(x*) – наименьшее (наибольшее) значение f(x) на Р. Если f(x) строго выпукла (вогнута), то х* - единственная точка глобального экстремума.

2.Пусть f(x) – выпуклая (вогнутая) функция на выпуклом множестве Р  Rⁿ и пусть grad f(x*)=0. Тогда х* -точка глобального минимума (максимума) f(x) на Р.