ПОУРОЧКА_6_КЛ_ФГОС. Урок 2 Наибольший общий делитель. Взаимно простые числа

• Название: Урок 2 Наибольший общий делитель. Взаимно простые числа
• Дата: 03.06.2022
• Размер: 2.22 Mb.
• Имя файла: ПОУРОЧКА_6_КЛ_ФГОС.doc
• Тип: Урок; #566970
• страница: 1 из 33

Урок 2

Наи­больший общий делитель. Взаимно простые числа
Цели: отрабатывать навыки разложения чисел на простые множители и нахождения наибольшего общего делителя; формирование чувства ответственности, воспитание самостоятельности учащихся, увеличение степени дисциплинированности, организованности, стимулирование «я – концепции», развитие общественно – активной личности, внедрение ситуации «успеха» в образовательный процесс, развитие индивидуальных особенностей учащихся. развитие умений применять математические знания для решения практических задач,формирование необходимости изучения математики для любой категории обучающихся.

Планируемые результат

Предметные: Освоить алгоритм нахождения НОД двух и трех чисел

Метапридметные: Коммуникативные: развить умение точно и грамотно выражать свои мысли, отстаивать свою точку зрения в процессе дискуссии.

Регулятивные: сформировать целевые установ­ки учебной деятельности, выстраивать алго­ритм действий.

Познавательные: выделять из множества один или не­сколько объектов, имеющих общие свойства

Личностные: сформировать устойчивую мотивацию к обучению

Основные понятия: разложение чисел на простые множители, нод.

Ход урока

I. Устная работа.

1. Решить № 154 (в; г; д).

2. Решить № 155, используя рисунок 7 учебника.

3. Какое число называют наибольшим общим делителем данных чисел?

Найдите наибольший общий делитель чисел: 1) 10 и 30; 2) 8 и 12; 3) 11 и 33; 4) 5 и 21; 5) 28 и 14; 6) 18; 27; 45; 7) 24; 36 и 48.

4. Какие два числа называют взаимно простыми? Найдите число, взаимно простое с числом: 6; 9; 15; 21; 25; 32; 40.

II. Выполнение упражнений.

1. Решить № 157 (б). Вызвать трех учеников к доске, каждый из них раскладывает одно из чисел на простые множители, остальные учащиеся в тетрадях раскладывают все данные числа на множители, а затем проверяют решение.

2. Решить задачу № 152 на доске и в тетрадях.

Решение.



3. Решить № 145 (б) с комментированием.

4. Решить № 148 (б; д) на доске и в тетрадях.

5. Решить № 147 (часть устно, некоторые письменно).

III. Итог урока.

Доказать, что взаимно простые числа: 35 и 72; 27 и 28.

Домашнее задание: п. 6; решить № 169 (б); № 170 (б; в), № 175, 1

Урок 3

Наи­больший общий делитель. Взаимно простые числа
Цели: отрабатывать навыки разложения чисел на простые множители и нахождения наибольшего общего делителя; воспитание математической речевой культуры, гигиеническое воспитание и формирование здорового образа жизни в целях сохранения психического, физического и нравственного здоровья человека, развитие интеграционных связей с другими дисциплинами, проведение анализа межпредметных связей, опора на морально-нравственные ценностные ориентиры, увеличение развивающих способностей, развитие нестандартного мышления, использование личностного и субъектного опыта.

Планируемые результаты:

Предметные: при­менять понятие «наибольший общий делитель» для решения за­дач

Метапридметные: Коммуникативные: научить слушать других, пытаться принимать другую точку зрения, быть гото­вым изменить свою. Регулятивные: формировать постановку учеб­ной задачи на основе соотнесения того, что уже известно и усвоено учащимися, и того, что еще неизвестно. Познавательные: приводить примеры в ка­честве доказательства выдвигаемых положений

Личностные: Сформировать навык ин­дивидуальной и коллектив­ной исследо­вательской деятельности

Основные понятия: разложение чисел на простые множители , нод

Ход урока

I. Устная работа.

1. Решить № 159 и № 162.

2. Решить задачу:

Какое наибольшее число одинаковых комплектов можно составить из елочных игрушек, если имеется:

8 зайцев, 24 лисицы, 16 морковок и 48 яблок? По скольку зайцев, лисиц, морковок и яблок будет в каждом комплекте?

II. Выполнение упражнений.

1. Решить № 151 на с. 26 учебника.

Ответ:

2. Решить № 148 (г; е) на доске и в тетрадях.

3. Решить задачу № 153.

Решение.



Или можно решить по-другому:

1) 424 + 477 = 901 (человек) поехали за город.

2) 901 : 53 = 17 (автобусов) было выделено.

4. Решить № 157 (2) (коллективное решение, а затем полусамостоятельно в тетрадях записывают решение задачи).

III. Самостоятельная работа (10–15 мин).

Вариант I.

1. Найдите наибольший общий делитель чисел 7425 и 12375.

2. Запишите два простых числа у, которые удовлетворяют неравенству 17 < y < 24.

3. Докажите, что 209 и 171 не взаимно простые.

4. На станции стоят три пассажирских поезда: в первом – 418 мест в купейных вагонах, во втором – 494, а в третьем – 456. Сколько купейных вагонов в каждом поезде, если в каждом вагоне одинаковое число мест и их число больше 20?

Вариант II.

1. Найдите наибольший общий делитель чисел 1456 и 1560.

2. Запишите два простых числа у, которые удовлетворяют неравенству 19 < y < 30.

3. Докажите, что числа 299 и 184 не взаимно простые.

4. На нефтебазу прибыло три состава цистерн с нефтью: в первом составе было 360 т нефти, во втором – 432 т, а в третьем – 792 т. Сколько цистерн с нефтью было в каждом составе, если в каждой цистерне одинаковое число тонн нефти и это число больше 50?

IV. Итог урока.Домашнее задание: решить № 170 (г), 171, 172, 174, 178 (а).

Урок 1

Тема: Наимень­шее общее кратное

Цели: Освоить понятие «наименьшее об­щее кратное». На­учиться находить НОК методом перебора. воспитание математической речевой культуры, гигиеническое воспитание и формирование здорового образа жизни в целях сохранения психического, физического и нравственного здоровья человека, развитие интеграционных связей с другими дисциплинами, проведение анализа межпредметных связей, опора на морально-нравственные ценностные ориентиры, увеличение развивающих способностей, развитие нестандартного мышления, использование личностного и субъектного опыта.

Планируемые результаты:Предметные: Освоить понятие «наименьшее об­щее кратное». На­учиться находить НОК методом перебора

Метапридметные: Коммуникативные: сформировать коммуника­тивные действия, направленные на структу­рирование информации по данной теме. Регулятивные: определять новый уровень отношения к самому себе как субъекту дея­тельности. Познавательные: выявлять особенности (ка­чества, признаки) разных объектов в процессе их рассматривания

Личностные: сформировать устойчивую мотивацию к изучению и закреплению нового

Основные понятия: понятие наименьшего общего кратного
Ход урока

I. Анализ самостоятельной работы.

1. Указать ошибки, допущенные учащимися при выполнении работы.

2. Решить на доске и в тетрадях задания, вызвавшие затруднения у учащихся.

II. Устная работа.

1. Решить № 186 (а; б).

2. Решить № 189 (а; б) и № 190 (г).

III. Объяснение нового материала.

1. Задача. Из порта А в порт В одновременно вышли два теплохода. Первый из них тратит на рейс туда и обратно 3 суток, а второй 4 суток. Через сколько суток оба теплохода окажутся снова вместе в порту А?

Решение.

Искомое число суток должно делиться и на 3, и на 4, то есть оно должно быть общим кратным чисел 3 и 4. Запишем кратные каждого из этих чисел в порядке возрастания:

Числа, кратные 3: 3; 6; 9; 12; 15; 18; 21; 24; 27; 30; 33; 36.

Числа, кратные 4: 4; 8; 12; 16; 20; 24; 28; 32; 36, …

Общие кратные чисел 3 и 4 (они подчеркнуты): 12; 24; 36; … Наименьшее из этих чисел – число 12. Значит, через 12 суток оба теплохода окажутся снова вместе в порту А. При этом первый теплоход совершит за это время 4 рейса туда и обратно (12 : 3 = 4), а второй – 3 рейса (12 : 4 = 3).

Наименьшее натуральное число, которое делится на каждое из данных натуральных чисел, называется наименьшим общим кратным.

2. Изучить по учебнику пункт 7 на с. 29–30.

3. Изучить правило нахождения наименьшего общего кратного для трех и более чисел.

4. Решить устно № 179 (а).

IV. Закрепление изученного материала.

1. Решить № 180 (а; б) с комментированием.

2. Решить № 181 (а; г; е) на доске и в тетрадях.

Решение.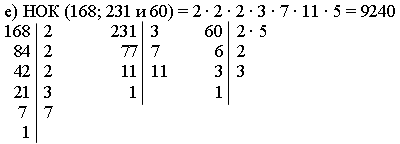



Ответ: 9240.

3. Повторение изученного ранее материала:

а) Решить № 195 и № 196 с комментированием.

б) Решить № 201, используя таблицу простых чисел на форзаце учебника.

V. Итог урока.

Вопросы:

1) Какое число называют наименьшим общим кратным натуральных чисел а и в?

2) Как найти наименьшее общее кратное нескольких чисел?

3) Какое число является наименьшим общим кратным чисел m и n, если число m кратно числу n?

Домашнее задание: изучить п. 7; решить № 202 (а), № 203 (а), № 206 (а; в).

Урок 2

Тема: Наимень­шее общее кратное

Цели: способствовать выработке навыков нахождения наименьшего общего кратного; учить применять наименьшее общее кратное чисел при решении задач; развивать логическое мышление учащихся, воспитание сознательного усвоения дисциплины, воспитание математической речевой культуры привитие навыков нравственного воспитания, воспитание трудолюбия, чувства коллективизма, привитие интереса к изучаемому предметуразвитие инициативы, познавательного интереса, обучение методам исследовательского поиска, развитие мыслительной деятельности, развитие практической направленности изучаемого материала.

Планируемые результаты Предметные: Освоить алгоритм нахождения НОК двух, трех чисел

Метапридметные: Коммуникативные: уметь точно и грамотно выражать свои мысли. Регулятивные: обнаруживать и формулиро­вать учебную проблему, составлять план вы­полнения работы. Познавательные: сопоставлять характери­стики объектов по одному или нескольким признакам, выявлять сходства и различия объектов

Личностные: Сформировать навык ин­дивидуальной и коллектив­ной исследо­вательской деятельности

Основные понятия: НОД и НОК
Ход урока

I. Устная работа.

1. Решить № 186 (в; г) и № 189 (в; г).

2. Укажите среди данных произведений разложение числа 700 на простые множители:

а) 4 · 5 · 5 · 7; б) 2 · 2 · 7 · 25; в) 2 · 2 · 5 · 5 · 7; г) 2 · 14 · 25.

Ответ: в).

3. Найдите НОД чисел 350; 420 и 210.

Ответ: 70.

4. Найдите НОК чисел 40; 60 и 70.

Ответ: 840.

II. Выполнение упражнений.

1. Решить № 179 (б) и № 180 (в) на доске и в тетрадях.

2. Решить № 181 (в) (коллективное обсуждение решения, а затем самостоятельное решение учащимися).

3. Решить задачу № 184.

Решение.

45 = 3 · 3 · 5; 60 = 2 · 5 · 2 · 3

НОК (45; 60) = 2 · 5 · 2 · 3 · 3 = 180.

Ответ: 180 м.

4. Решить задачу.

Какой наименьшей длины ленту должна купить Мальвина, чтобы разрезать ее на ленты по 35 см или по 50 см, не получив обрезков?

Решение.

35 = 5 · 7; 50 = 2 · 5 · 5; НОК (35; 50) = 2 · 5 · 5 · 7 = 350.

Ответ: 350 см = 3 м 50 см.

5. Проверить равенство НОК (а; в) · НОД (а; в) = а · в, если а = 28, в = 21.

Решение.

28 = 2 · 2 · 7; 21 = 3 · 7.

НОД (28; 21) = 7; НОК (28; 21) = 2 · 2 · 7 · 3 = 84.

а · в = 28 · 21 = 588; НОК (а; в) · НОД (а; в) = 84 · 7 = 588.

Равенство верно.

III. Повторение ранее изученного материала.

1. Решить № 191.

2. Как находится среднее арифметическое чисел?

Решить № 198.

3. Решить задачу № 199.

Решение.

Пусть второе число равно х, тогда первое число 2х.

(х + 2х) : 2 = 54

3х = 54 · 2

3х = 108

х = 108 : 3

х = 36.

Второе число равно 36, первое число 72.

Ответ: 72 и 36.

4. Самостоятельно решить задание –

найти наибольший общий делитель чисел:

а) 465 и 870; б) 645 и 680.

IV. Итог урока.

1. Повторить правило нахождения НОК.

2. Найти наименьшее общее кратное чисел (устно):

а) 3 и 7; б) 8 и 6; в) 9 и 14; г) 180 и 120.

Домашнее задание: изучить п. 7; решить № 202 (б; в), № 204, № 207, № 210 (а).

Урок 3

Тема: Наимень­шее общее кратное

Цели: тренировать учащихся в нахождении НОД и НОК чисел при выполнении упражнений, формирование чувства ответственности, воспитание самостоятельности учащихся, увеличение степени дисциплинированности, организованности, стимулирование «я – концепции», развитие общественно – активной личности, внедрение ситуации «успеха» в образовательный процесс, развитие индивидуальных особенностей учащихся. развитие умений применять математические знания для решения практических задач, формирование необходимости изучения математики для любой категории обучающихся.
Планируемые результаты Предметные: научиться приме­нять НОК для ре­шения задач

Метапридметные: Коммуникативные: научить критично от­носиться к своему мнению, с достоинством признавать ошибочность своего мнения (если оно таково) и корректировать его. Регулятивные: осознавать учащимся уровень и качество усвоения результата. Познавательные: уметь осуществлять выбор наиболее эффективных способов решения образовательных задач в зависимости от кон­кретных условий

Личностные: сформировать устойчивую мо­тивацию к индивидуальной деятельности по самостоя­тельно состав­ленному плану

Основные понятия: НОД и НОК

Ход урока

I. Устная работа.

1. Решить № 188, 189 (д; е) и № 192.

2. Найти наибольший общий делитель и наименьшее общее кратное чисел:

а) 5 и 25; б) 25 и 75; в) 8; 12 и 24; г) 18; 27 и 54; д) 60; 40; 120; е) 2 и 3; ж) 8 и 9; з) 5; 8 и 3; и) 120; 180 и 360.

II. Тренировочные упражнения.

1. Решить № 180 (г) с комментированием.

2. Решить № 181 (д) на доске и в тетрадях.

3. Решить № 182 с обсуждением и решением в тетрадях. Записать вывод: наименьшее общее кратное двух взаимно простых чисел равно произведению этих чисел.

4*. Решить задачу: Саша ходит в бассейн один раз в 3 дня, Вася – в 4 дня, а Ваня – в 5 дней.

Они встретились в бассейне в этот понедельник. Через сколько дней и в какой день недели они встретятся снова?

Решение.

НОК (3; 4; 5) = 60. Через 60 дней, в пятницу (60 : 7 = 8 недель и 4 дня пройдет) они встретятся снова.

Ответ: через 60 дней, в пятницу.

5. Решить самостоятельно задачу:

Какой наименьшей длины должна быть доска, чтобы ее можно было разрезать поперек на части, равные 20 см или 27 см, не получив обрезков?

НОК (20; 27) = 540.

Длина доски должна быть 540 см = 5 м 40 см.

Ответ: 5 м 40 см.

6. Решить № 175 на доске и в тетрадях. Сделать вывод.

III. Самостоятельная работа (10–15 мин).

Вариант I.

1. Найдите наименьшее общее кратное чисел:

а) 18 и 27; б) 7875 и 4725.

2. На базар привезли арбузы. Если их считать десятками, то получится целое число десятков. Если их считать дюжинами (по 12), то опять получится целое число дюжин. Сколько арбузов привезли на базар, если их больше 300, но меньше 400?

3. Проверьте равенство НОК (m; n) = если m = 35, n = 49.

Вариант II.

1. Найдите наименьшее общее кратное чисел:

а) 40 и 56; б) 7425 и 4455.

2. Солдаты выстроились в ряды, по 12 человек в каждом, а затем перестроились по 8 человек в ряду. Сколько было солдат, если их больше 180, но меньше 200?

3. Проверьте равенство НОД (с; d) = если с = 42, d = 35.

IV. Итог урока.

Повторить выводы упражнений № 182 и 183, придумать свои примеры.

Домашнее задание: решить № 202 (г), № 205, № 208, № 210 (б).

Урок 4

Тема: Наимень­шее общее кратное

Цели: тренировать учащихся в нахождении НОД и НОК чисел при выполнении упражнений воспитание математической речевой культуры, гигиеническое воспитание и формирование здорового образа жизни в целях сохранения психического, физического и нравственного здоровья человека, развитие интеграционных связей с другими дисциплинами, проведение анализа межпредметных связей, опора на морально-нравственные ценностные ориентиры, увеличение развивающих способностей, развитие нестандартного мышления, использование личностного и субъектного опыта.